leetcode.37 解數獨
阿新 • • 發佈:2018-12-21
編寫一個程式,通過已填充的空格來解決數獨問題。
一個數獨的解法需遵循如下規則:
數字 1-9 在每一行只能出現一次。
數字 1-9 在每一列只能出現一次。
數字 1-9 在每一個以粗實線分隔的 3x3 宮內只能出現一次。
空白格用 ‘.’ 表示。
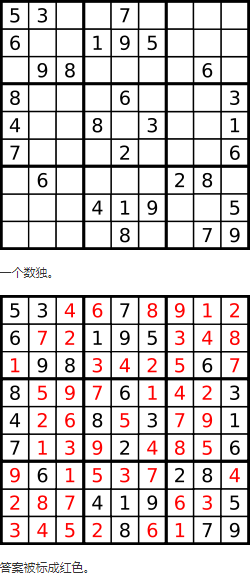
Note:
- 給定的數獨序列只包含數字 1-9 和字元 ‘.’ 。
- 你可以假設給定的數獨只有唯一解。
- 給定數獨永遠是 9x9 形式的。
思路:遞迴搜尋,注意好判斷可放置數字的條件和獲取下一個放置點的方法,主要還是理清好如何去遞迴搜尋會比較好處理。
private static class Node{ public int i; public int j; } public void solveSudoku(char[][] board) { char[][] chars = new char[board.length][board.length]; for (int i = 0; i < chars.length; i++) { for (int j = 0; j < chars.length; j++) { chars[i][j] = board[i][j]; } } if(chars[0][0] == '.') dfs(board, 0, 0, chars); else{ Node node = getNext(chars,0,0); dfs(board,node.i,node.j,chars); } } public boolean dfs(char[][] data, int i, int j, char[][] flag) { boolean b = false; for (int target = 1; target <= 9; target++) { boolean res = place(i, j, data, flag, String.valueOf(target).charAt(0)); if (res) { data[i][j] = String.valueOf(target).charAt(0); Node node = getNext(flag,i,j); if(node != null){ b = dfs(data, node.i, node.j, flag); } else{ return true; } if (b) { return true; }else{ data[i][j] = '.'; } } } return false; } public boolean judge(int i, int j) { if (0 <= i && i < 9 && j >= 0 && j < 9) return true; return false; } public boolean place(int i, int j, char[][] data, char[][] flag, char target) { if (judge(i, j) && flag[i][j] == '.') { for (int k = 0; k < 9; k++) { if (data[i][k] == target) return false; if (data[k][j] == target) return false; } //判斷九個區域 if(i >= 0 && i <= 2 && j >=0 && j <= 2){ for(int k = 0;k <=2;k++){ for(int l = 0;l <= 2;l++){ if(data[k][l] == target) return false; } } } else if(i>=0 && i <=2 && j>=3 && j<= 5){ for(int k = 0;k <= 2;k++){ for(int l = 3;l <= 5;l++){ if(data[k][l] == target) return false; } } } else if(i>=0 && i <=2 && j>=6 && j<= 8){ for(int k = 0;k <= 2;k++){ for(int l = 6;l <= 8;l++){ if(data[k][l] == target) return false; } } } // if(i >= 3 && i <= 5 && j >=0 && j <= 2){ for(int k = 3;k <=5;k++){ for(int l = 0;l <= 2;l++){ if(data[k][l] == target) return false; } } } else if(i>=3 && i <=5 && j>=3 && j<= 5){ for(int k = 3;k <= 5;k++){ for(int l = 3;l <= 5;l++){ if(data[k][l] == target) return false; } } } else if(i>=3 && i <=5 && j>=6 && j<= 8){ for(int k = 3;k <= 5;k++){ for(int l = 6;l <= 8;l++){ if(data[k][l] == target) return false; } } } // if(i >= 6 && i <= 8 && j >=0 && j <= 2){ for(int k = 6;k <=8;k++){ for(int l = 0;l <= 2;l++){ if(data[k][l] == target) return false; } } } else if(i>=6 && i <=8 && j>=3 && j<= 5){ for(int k = 6;k <= 8;k++){ for(int l = 3;l <= 5;l++){ if(data[k][l] == target) return false; } } } else if(i>=6 && i <=8 && j>=6 && j<= 8){ for(int k = 6;k <= 8;k++){ for(int l = 6;l <= 8;l++){ if(data[k][l] == target) return false; } } } return true; } else { return false; } } public Node getNext(char[][] flag,int i,int j){ boolean b = false; Node node = new Node(); for(int ii = 0; ii < 9;ii++){ for (int jj = 0; jj<9;jj++){ if(ii == i && jj == j){ b = true; continue; } if(flag[ii][jj] == '.' && b){ node.i = ii; node.j = jj; return node; } } } return null; }
