功率譜和頻譜

先簡要說計算：
功率譜：訊號先自相關再作FFT
頻 譜：訊號直接作FFT

功率譜：
訊號的傳播都是看不見的，但是它以波的形式存在著，這類訊號會產生功率，單位頻帶的訊號功率就被稱之為功率譜。它可以顯示在一定的區域中訊號功率隨著頻率變化的分佈情況。

功率譜可以從兩方面來定義：
一個 是自相關函式的傅立葉變換；（維納辛欽定理）
另一個 是時域訊號傅氏變換模平方然後除以時間長度。（來自能量譜密度）
根據parseval定理，訊號傅氏變換模平方被定義為能量譜，能量譜密度在時間上平均就得到了功率譜。

頻譜：
頻譜是常常指訊號的Fourier變換。

（1-7 作者：Yorkxu）轉載的理解：
（1）訊號通常分為兩類：能量訊號和功率訊號；

• 能量訊號：又稱能量有限訊號，是指在所有時間上總能量不為零且有限的訊號。
• 功率訊號：它的能量為無限大，它對通訊系統的效能有很大影響，決定了無線系統中發射機的電壓和電磁場強度。

（2）一般來講，能量訊號其傅氏變換收斂（即存在），而功率訊號傅氏變換通常不收斂（當然，若訊號存在週期性，可引入特殊數學函式（Delta）表徵傅氏變換的這種非收斂性）；

（3）訊號是資訊的搭載工具，而資訊與隨機性緊密相關，所以實際訊號多為隨機訊號，這類訊號的特點是狀態隨機性隨時間無限延伸，其樣本能量無限

（4）若撇開搭載資訊的有用與否，隨機訊號又稱隨機過程，很多噪聲屬於特殊的隨機過程，它們的某些統計特性具有平穩性，其均值和自相關函式具有平穩性。對於這樣的隨機過程，自相關函式蛻化為一維確定函式，前人證明該確定相關函式存在傅氏變換；

（5）能量訊號頻譜通常既含有幅度也含有相位資訊；幅度譜的平方（二次量綱）又叫能量譜（密度），它描述了訊號能量的頻域分佈；功率訊號的功率譜（密度）描述了訊號功率隨頻率的分佈特點（密度：單位頻率上的功率），業已證明，平穩訊號功率譜密度恰好是其自相關函式的傅氏變換。對於非平穩訊號，其自相關函式的時間平均（對時間積分，隨時變性消失而再次退變成一維函式）與功率譜密度仍是傅氏變換對；

（6）實際中我們獲得的往往僅僅是訊號的一段支撐，此時即使訊號為功率訊號，截斷之後其傅氏變換收斂，但此變換結果嚴格來講不屬於任何“譜”（進一步分析可知它是樣本真實頻譜的平滑：卷積譜）；

（7）對於（6）中所述變換若取其幅度平方，可作為平穩訊號功率譜（密度）的近似，是為經典的“週期圖法”；

補充：（8） 一個訊號的頻譜,只是這個訊號從時域表示轉變為頻域表示,只是同一種訊號的不同的表示方式而已；而功率譜是從能量的觀點對訊號進行的研究,其實頻譜和功率譜的關係歸根揭底還是訊號和功率,能量等之間的關係。

譜估計

功率譜估計一般分成兩大類：
經典譜估計，也稱為非引數譜估計。
現代譜估計，也稱為引數譜估計。

根據維納-辛欽定理，平穩隨機過程的功率譜等於自相關序列的DTFT:

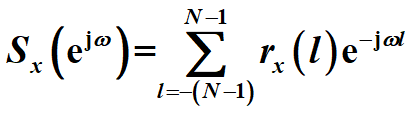
matlab做訊號預處理

一開始博主錄音了內容為“現代訊號處理”的話音，並存為單聲道wav做處理，但是因為訊號過長 且發音不標準 導致實驗效果受影響，所以減少話音長度，僅僅讀取“代”的話音作為分析樣本。
上原始碼：

close all;clear all;
% read speech waveform from a file
[s, fs] = audioread('代.wav');

% set analysis parameters, pre-emphasise and windowing
%根據話音位置，取8192可以把話音主要部分加入其中
N = 8192;
Nfft = 8192;
n0 = 1000;
x = s(n0 : n0+N-1);
x1 = filter([1 -0.97], 1, x); %預加重 濾波器
%作用：消除6dB/oct（分貝/倍頻程）的跌落，使語音訊號的頻譜變得平坦。

w = (window('hamming', N));
xw = x1 .* w; %加窗
 
% Estimate PSD of the short-time segment
Sxw = fft(xw, Nfft);
Sxdb = 20*log10(abs(Sxw(1 : Nfft/2))) - 10*log10(N);
%Sxdb 功率譜：時域fft取模平方後除以訊號的長度 轉換成db
figure;
subplot(4,1,1);
plot(s);  xlim([0 length(s)]); ylim([-0.65 0.65]);
ylabel('Amplitude');  xlabel('Time (n)');
subplot(4,1,2);
plot(xw); xlim([0 length(x)]); ylim([-0.225 0.225]);
ylabel('Amplitude');  xlabel('Time (n)'); 

f = (0 : Nfft/2-1)*fs / Nfft / 1000;%取前一半 後一半是翻轉
subplot(2,1,2);
plot(f, Sxdb);
ylabel('Magnitude (dB)');  xlabel('Frequency (kHz)');

效果圖：

從上至下：原始話音、經過預處理後的話音、話音的理論上的功率譜

經典譜估計法1：相關圖法

為了減少譜估計的方差，採用長度為2M-1的窗函式對自相關函式進行擷取（聯絡上式），得


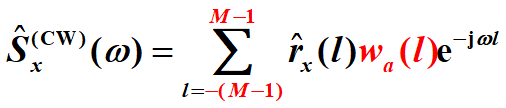
可使用矩形窗和三角窗。

估計自相關序列：

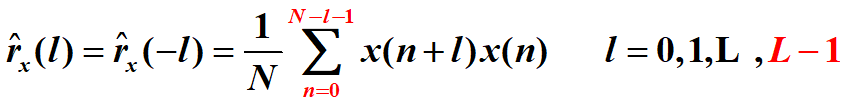
這裡解釋一下，下標之所以是0~L-1 且r關於l=0對稱，是因為數學推導：把-l帶入r(l)依然能得到後面式子的結果。（問的老師）
構成加窗自相關序列：

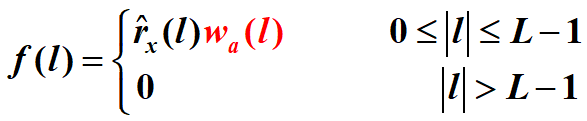
計算序列 f(l) 的NFFT（一般選NFFT >2L-1）點DFT/FFT，即為功率譜估計的取樣值:

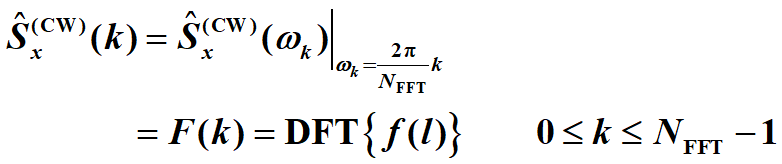
r = zeros(2*N/2-1, 1);%(-(N/2-1)~(N/2-1))共2L-1個點 計算自相關
for k = 1 : N/2
    x1 = x(k : N);
    x2 = x(1 : N+1-k);
    r(N/2+k-1) = x1' * x2 / N;
    r(N/2-k+1) = r(N/2+k-1);    %r(-k) = r(k)
end

rx = r ;
Sxz1 = fft(rx, Nfft);
Sxdbz1 = 10*log10(abs(Sxz1(1 : Nfft/2)));%轉換成db

subplot(4,1,3);
plot(f, Sxdbz1);
ylabel('Magnitude (dB)');  xlabel('Frequency (kHz)');
title('Correlogram (Rectangle)');

%----------------相關圖法 三角窗 --------------%
w = triang(2*N/2-1)'; %三角窗 加窗後效果
rx = r .* w';
Sxz2 = fft(rx, Nfft);
Sxdbz2 = 10*log10(abs(Sxz2(1 : Nfft/2)));
subplot(4,1,4);
plot(f, Sxdbz2);
ylabel('Magnitude (dB)');  xlabel('Frequency (kHz)');
 title('Correlogram (Triangular)');

效果圖：
下兩幅是相關圖法的結果，分別使用了矩形窗和三角窗

經典譜估計法2：週期圖法

由本文開始給的定義，功率譜的計算可以是時域訊號傅氏變換模平方然後除以時間長度。

但是此方法，當週期圖的方差(當N較大時)，方差：


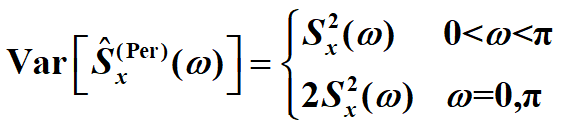
（可以用多次實驗取平均來緩解）
改進：

• 多個週期圖求平均
  把資料記錄切分為K個分段，分別求週期圖，然後求平均。每段長L，偏移量D
  
  
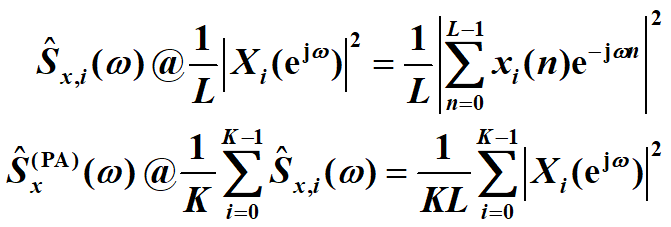
  （上式@號其實是=號）
  PA: 週期圖求平均；
  Bartlett方法：D=L;
  Welch方法： D=L/2

Bartlett方法就是把資料分D段，每段fft模平方除以每段長度，再把D段的s相加再平均。

Welch方法就是有重複的分段，具體如下圖：

%----------------週期圖法 Bartlett譜估計--------------%
Sx = zeros(1, Nfft/2);K = 4; L = N/K;
for k = 1 : K
    ks = (k-1)*L + 1;
    ke = ks + L - 1;
    X = fft(x(ks:ke), Nfft);
    X = (abs(X)).^2;          %週期圖法這裡要abs + 平方 注意
    for i = 1 : Nfft/2
        Sx(i) = Sx(i) +X(i);
    end
end

for i = 1 : Nfft/2
    Sx(i) = 10*log10(Sx(i)/(K*L));
end


figure;
subplot(4,1,1);
plot(f, Sx);
ylabel('Magnitude (dB)');  xlabel('Frequency (kHz)');
title('Bartlett Estimate, N=4096, K=4, D=L=1024')

%----------------週期圖法 Welch譜估計--------------%
Nfft = 8192; 
K = 4; 
D = fix(Nfft/2 / (K+1));%向0方向靠攏取整 分為K+1格，可以重疊K次做fft
L = 2*D;
Sxw = zeros(1, Nfft/2);
w = (window('hamming', L))';
for k = 1 : K
    ks = (k-1)*D + 1;
    ke = ks + L - 1;
    xk = x(ks:ke) .* w; %時域加窗
    X = fft(xk, Nfft);
    X = (abs(X)).^2;
    for i = 1 : Nfft/2
        Sxw(i) = Sxw(i) + X(i); %這裡只取前N/2個點 因為後N/2個點是前的翻轉
    end
end
for i = 1 : Nfft/2
    Sxw(i) = 10*log10(Sxw(i)/(K*L)); %轉換成db
end
subplot(4,1,2);  plot(f, Sxw);
ylabel('Magnitude (dB)'); xlabel('Frequency (kHz)');
title('Welch Estimate, N=4096, K=4, D=819, L=1638');

效果圖是效果圖的第一和第二張。

語譜圖

語音訊號的時頻分佈為定義在二維空間的函式，把時頻分佈畫成二維灰度影象的形式，即為語譜圖。

MATLAB 函式
[S, f, t, P] = spectrogram(x, window, noverlap, nfft, fs)；
效果圖

 %--------------語譜圖--------------%
 bw = 300;
nwin = round(2*fs/bw); 
%nfft = 512;
nfft = 1024;
xy = filter([1 -0.97], 1, s);
noverlap = nwin - round(length(s) / 500);

% compute and show
figure;
[S, f,  t, P] = spectrogram(xy, nwin, noverlap, nfft, fs);
surf(t, f/1000, 10*log10(abs(P)), 'EdgeColor', 'none');
axis xy; axis tight; colormap(jet); view(0, 90);
xlabel('Time (s)'); ylabel('Frequency (kHz)');
%title('Broadband Spectrogram');
title('Narrowband Spectrogram');

END

致敬北郵尹霄麗老師！公式和很多概念都引用老師現代訊號處理課程的教案，老師上課講的很細緻很明白，很榮幸能作為老師的學生。