上一篇文章我們寫了什麼是常量，這篇文章我們就一起來介紹一下進位制。

1.進位制：進位制也就是進位計數制，是人為定義的帶進位的計數方法（有不帶進位的計數方法，比如原始的結繩計數法，唱票時常用的“正”字計數法，以及類似的tally mark計數）。 對於任何一種進位制---X進位制，就表示每一位置上的數運算時都是逢X進一位。 十進位制是逢十進一，十六進位制是逢十六進一，二進位制就是逢二進一，以此類推，x進位制就是逢x進位。

2. 一個位元組用byte表示得話：

   1bety（位元組）=8bit（位元位）

   1k(K)  = 1024b（位元位）

   1m(兆)=1024k

   1g   =1024m（兆）

   1t   = 1024g 

小知識拓展：

  我們都知道電腦正常都是500G，但是實際情況並不是是465G,那麼為什麼呢？

 其實生成廠商是以1000為進位制，而我們計算機是以1024為進位制,500g以廠商1000為進位制換算到byte，在以計算機1024進位制換算到g，讓我們來看看。

 500g=500*1000(m)*1000(k)*1000(b) /1024(b)/1024(k)/1024(m) =最後實際電腦記憶體 

3.進位制越大，表現形式越短。

4.不同進位制在java中得表型形式：

  二進位制：0b100(b可以大寫也可以小寫)

  八進位制：0100

  十進位制：100

  十六進位制：0x100(x可以大寫也可以小寫)

5.進位制轉換：我們可以看見二進位制，八進位制，十進位制，十六進位制，轉換成十進位制得結果分別是4，64，100，256 ，特別注意輸出語句括號內容不能加雙引號，因為之前我們講過常量，加上雙引號其值事不能發生改變得，這樣系統就不能自動計算了。

十進位制到十進位制轉換原理：

12345=10000+2000+300+40+5=1*10^4+2*10^3+3*10^2+4*10^1+5*10^0

總結： 

       係數：就是每一位是得資料

       基數：X進位制，基數就是X

       權數：在右邊，從0開始編號，對應位數上得編號即為該位得權

      結果：把係數*基數得權次冪相加即可

例如：二級制轉十進位制

        0b100=1*2^2+0*2^1+0*2^0=4

           八進位制轉十進位制

        0100=1*8^2+0*8^1+0*8^0=64

          十六進位制轉十進位制

       0x100=1*16^2+0*16^1+0*16^0=256

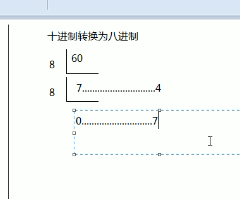
6.十進位制到任意進位制轉換原理： 除積倒去餘  

   12345/10=1234.。。。。5

   1234/10  =123.。。。。  4

   123/10    =12.。。。。。3

   12/10      =1.。。。。。  2

   1/10        =0.。。。。。  1

未完待續。。。。。。