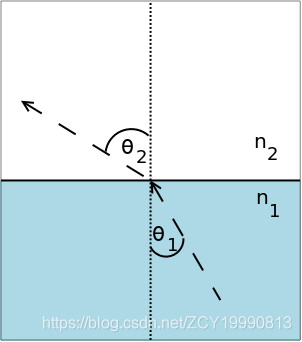
A submarine is using a communications laser to send a message to a jet cruising overhead. The sea surface is flat. The submarine is cruising at a depth d below the surface. The jet is at height h above the sea surface, and a horizontal distance x from the sub. The submarine turns toward the jet before starting communications, but needs to know the angle of elevation, φ, at which to aim the laser.When the laser passes from the sea into the air, it is refracted (its path is bent). The refraction is described by Snell’s law, which says that light approaching the horizontal surface at an angle θ 1 , measured from the vertical, will leave at an angle θ 2 , given by the formula sin θ 1/n 1=sin θ 2/n 2
where n 1 and n 2 are the respective refraction indices of the water and air.(The refraction index of a material is inversely proportional to how fast light can travel through that material.)

Input
Each test case consists of a single line of input containing 5 space-separated floating point numbers:
• d, the depth of the submarine (specifically, of the laser emitter) in feet, 1 ≤ d ≤ 800
• h, the height of the plane in feet, 100 ≤ h ≤ 10, 000
• x, the horizontal distance from the sub to the plane in feet, 0 ≤ x ≤ 10, 000
• n 1 , the refractive index of water, 1.0 < n 1 ≤ 2.5
• n 2 , the refractive index of air, 1.0 ≤ n 2 < n 1
Input ends with a line containing 5 zeroes (0 0 0 0 0).ACM-ICPC Live Archive: 7292 – Refract Facts 2/2
Output
For each test case, print a single line containing the angle of elevation φ at which the submarine should aim its laser to illuminate the jet.The angle should be displayed in degrees and rounded to the closest 1/100 of a degree. Exactly two digits after the decimal point should be displayed.

Sample Input
600
600
400
0 0
600 1000 1.333 1.01
1200 4000 1.5 1.01
100 10000 2.5 1.01
0 0 0
Sample Output
44.37
11.51
2.30

題意：求fai角度，知道了海平面與飛機的距離h,潛艇與海平面的距離d,水平距離x,兩個角度的比例 n1 n2關係。

思路：二分，fai角度0到90度的取值範圍，求出來H大了，說明fai求大了，應該從0到45範圍中，反之45到90的範圍。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#define PI acos(-1)
const int maxn = 26;
using namespace std;
typedef long long ll;
double d,h,x,n1,n2;
double _mid(double l,double r)
{
    double fai,x2,x1,seita1,seita2,sinseita1,sinseita2,H;
    while(r-l>0.001)
    {
        fai=(l+r)/2.0;
        x2=d/tan(fai*PI/180);
        x1=x-x2;
        seita1=90.0-fai;
        sinseita2=sin(seita1*PI/180)*n2/n1;
        seita2=asin(sinseita2)*180/PI;
        H=x1/tan(seita2*PI/180);
        if(H>h)
            r=fai;
        else
            l=fai;
    }
    return l;
}
int main()
{
    while(cin>>d>>h>>x>>n1>>n2)
    {
        if(d==0&&h==0&&x==0&&n1==0&&n2==0)
            break;
        double l=0.00,r=90.00;
        double ans=_mid(l,r);
        printf("%.2lf\n",ans);
    }
    return 0;
}