資料結構(十五)
阿新 • • 發佈:2018-12-22
最小生成樹問題
1. 什麼是最小生成樹
- 是一棵樹
- 無迴路
- |V|個頂點一定有 |V|-1 條邊
- 是生成樹
- 不唯一
- 包含全部頂點
- |V|-1 條邊都在圖裡
- 邊的權值和最小
2. 貪心演算法
- 什麼是 “貪”:每一步都是最好的
- 什麼是 “好”:權重最小的邊
- 需要約束:
- 只能用圖裡有的邊
- 只能正好用掉 |V|-1 條邊
- 不能有迴路
1. Prim 演算法

void Prim(){
MST = {s}; // parent[s] = -1
while(1){
V = 未收錄頂點中dist最小者; // dist[V] = E<V,W> 或 正無窮 時間複雜度:T = O(|V|) —— 稀疏圖合算
#include<iostream>
#include<vector>
#define INF 100000
#define MaxVertex 105
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int parent[MaxVertex]; // 並查集
int dist[MaxVertex]; // 距離
int Nv; // 結點
int Ne; // 邊
int sum; // 權重和 2. Kruskal 演算法
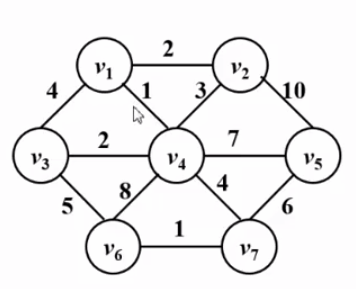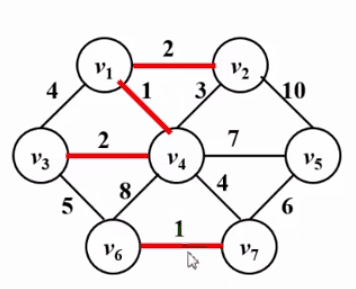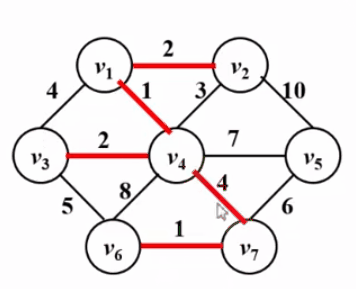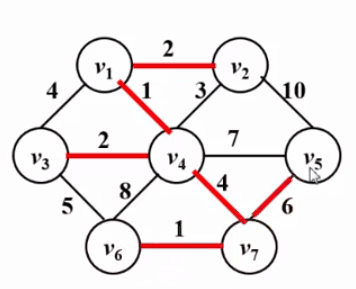
void Kruskal ( Graph G ){
MST = { };
while ( MST 中不到|V|-1條邊 && E中還有邊 ) {
從 E 中取一條權重最小的邊 E<V,W>; // 最小堆
將 E<V,W> 從 E 中刪除;
if ( E<V,W> 不在 MST 中構成迴路 ) // 並查集
將 E<V,W> 加入MST;
else
徹底無視 E<V,W>;
}
if ( MST 中不到|V|-1條邊 )
Error("圖不連通");
}
時間複雜度:T = O(|E|log|E|) —— 稀疏圖合算
#include<iostream>
#include<string>
#include<vector>
#include<queue>
#define INF 100000
#define MaxVertex 105
typedef int Vertex;
int G[MaxVertex][MaxVertex];
int parent[MaxVertex]; // 並查集最小生成樹
int Nv; // 結點
int Ne; // 邊
int sum; // 權重和
using namespace std;
struct Node{
Vertex v1;
Vertex v2;
int weight; // 權重
// 過載運算子成最大堆
bool operator < (const Node &a) const
{
return weight>a.weight;
}
};
vector<Node> MST; // 最小生成樹
priority_queue<Node> q; // 最小堆
// 初始化圖資訊
void build(){
Vertex v1,v2;
int w;
cin>>Nv>>Ne;
for(int i=1;i<=Nv;i++){
for(int j=1;j<=Nv;j++)
G[i][j] = 0; // 初始化圖
parent[i] = -1;
}
// 初始化點
for(int i=0;i<Ne;i++){
cin>>v1>>v2>>w;
struct Node tmpE;
tmpE.v1 = v1;
tmpE.v2 = v2;
tmpE.weight = w;
q.push(tmpE);
}
}
// 路徑壓縮查詢
int Find(int x){
if(parent[x] < 0)
return x;
else
return parent[x] = Find(parent[x]);
}
// 按秩歸併
void Union(int x1,int x2){
x1 = Find(x1);
x2 = Find(x2);
if(parent[x1] < parent[x2]){
parent[x1] += parent[x2];
parent[x2] = x1;
}else{
parent[x2] += parent[x1];
parent[x1] = x2;
}
}
void Kruskal(){
// 最小生成樹的邊不到 Nv-1 條且還有邊
while(MST.size()!= Nv-1 && !q.empty()){
Node E = q.top(); // 從最小堆取出一條權重最小的邊
q.pop(); // 出隊這條邊
if(Find(E.v1) != Find(E.v2)){ // 檢測兩條邊是否在同一集合
sum += E.weight;
Union(E.v1,E.v2); // 並起來
MST.push_back(E);
}
}
}
void output(){
cout<<"被收錄順序:"<<endl;
for(Vertex i=0;i<Nv;i++)
cout<<MST[i].weight<<" ";
cout<<"權重和為:"<<sum<<endl;
for(Vertex i=1;i<=Nv;i++)
cout<<parent[i]<<" ";
cout<<endl;
}
int main(){
build();
Kruskal();
output();
return 0;
}
