一 序：

   之前的文章<跳躍表的原理> 已經整理過，本篇看下redis的具體實現。以下摘自書上的介紹：

  跳躍表（skiplist）是一種有序資料結構， 它通過在每個節點中維持多個指向其他節點的指標， 從而達到快速訪問節點的目的。跳躍表支援平均 O(\log N) 最壞 O(N) 複雜度的節點查詢， 還可以通過順序性操作來批量處理節點。
在大部分情況下， 跳躍表的效率可以和平衡樹相媲美， 並且因為跳躍表的實現比平衡樹要來得更為簡單， 所以有不少程式都使用跳躍表來代替平衡樹。
Redis 使用跳躍表作為有序集合鍵的底層實現之一： 如果一個有序集合包含的元素數量比較多， 又或者有序集合中元素的成員（member）是比較長的字串時， Redis 就會使用跳躍表來作為有序集合鍵的底層實現。
和連結串列、字典等資料結構被廣泛地應用在 Redis 內部不同， Redis 只在兩個地方用到了跳躍表， 一個是實現有序集合鍵， 另一個是在叢集節點中用作內部資料結構， 除此之外， 跳躍表在 Redis 裡面沒有其他用途。 

Redis的跳躍表實現跟WilliamPugh在"Skip Lists: A Probabilistic Alternative to Balanced Trees"中描述的跳躍表演算法類似，只是有三點不同：

•  允許重複分數；
•  排序不止根據分數，還可能根據成員物件（當分數相同時）；
• 有一個前繼指標，因此在第1層，就形成了一個雙向連結串列，從而可以方便的從表尾向表頭遍歷，用於ZREVRANGE命令的實現。

二  跳錶結構：

    Redis跳躍表的相關結構體定義3.12版本在server.h,老版本說在redis.h，新版本沒看。

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
	// member 物件
    robj *obj;
	// 分值
    double score;
	// 後退指標
    struct zskiplistNode *backward;
	// 層
    struct zskiplistLevel {
		// 前進指標
        struct zskiplistNode *forward;
		// 節點在該層和前向節點的距離
        unsigned int span;
    } level[];
} zskiplistNode;
 
typedef struct zskiplist {
	// 頭節點，尾節點
    struct zskiplistNode *header, *tail;
	// 節點數量
    unsigned long length;
	// 目前表內節點的最大層數
    int level;
} zskiplist;
 

       obj是該結點的成員物件指標，score是該物件的分值，是一個浮點數，跳躍表中的所有結點，都是根據score從小到大來排序的。   同一個跳躍表中，各個結點儲存的成員物件必須是唯一的，但是多個結點儲存的分值卻可以是相同的：分值相同的結點將按照成員物件的字典順序從小到大進行排序。

       level陣列是一個柔性陣列成員，它可以包含多個元素，每個元素都包含一個層指標(level[i].forward)，指向該結點在本層的後繼結點。該指標用於從表頭向表尾方向訪問結點。可以通過這些層指標來加快訪問結點的速度。
  Redis中的跳躍表，與普通跳躍表的區別之一，就是包含了層跨度(level[i].span)的概念。這是因為在有序集合支援的命令中，有些跟元素在集合中的排名有關，比如獲取元素的排名，根據排名獲取、刪除元素等。通過跳躍表結點的層跨度，可以快速得到該結點在跳躍表中的排名。
      每個結點還有一個前繼指標backward。可用於從表尾向表頭方向訪問結點。通過結點的前繼指標，組成了一個普通的連結串列。因為每個結點只有一個前繼指標，所以只能依次訪問結點，而不能跳過結點。

      zskiplist 跟之前普通跳錶沒啥不同，頭、尾、節點數量，最大層數。下面是跳錶結構：書上有個圖，我覺得不如網上這個直觀些。個人覺得書上那種 高高低低的有曲線的圖容易暈。

冪次定律（powerlaw）

三 跳錶分析

  3.1 隨機性

  之前的在整理跳錶模型的時候，跳錶新增節點的高度或者層數是有隨機數確定的。直接是0.5的概率，那麼redis的冪次定律（powerlaw）事怎麼一會事呢？看下程式碼，在t_zet.c

/* Returns a random level for the new skiplist node we are going to create.
 *
 * 返回一個隨機值，用作新跳躍表節點的層數。
 *
 * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
 * (both inclusive), with a powerlaw-alike distribution where higher
 * levels are less likely to be returned. 
 *
 * 返回值介乎 1 和 ZSKIPLIST_MAXLEVEL 之間（包含 ZSKIPLIST_MAXLEVEL），
 * 根據隨機演算法所使用的冪次定律，越大的值生成的機率越小。
 *
 * T = O(N)
 */
int zslRandomLevel(void) {
    int level = 1;

    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;

    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

   一開始我是看不懂的，gqtcgq 的文章介紹了細節。貼一下分析及測試程式碼，對於c程式碼，本地也沒有 環境，網上找了線上除錯的。下面貼一下分析及程式碼。

       這裡的ZSKIPLIST_P是0.25。上述程式碼中，level初始化為1，然後，如果持續滿足條件：(random()&0xFFFF)< (ZSKIPLIST_P * 0xFFFF)的話，則level+=1。最終調整level的值，使其小於ZSKIPLIST_MAXLEVEL。

         理解該演算法的核心，就是要理解滿足條件：(random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)的概率是多少？

         random()&0xFFFF形成的數，均勻分佈在區間[0,0xFFFF]上，那麼這個數小於(ZSKIPLIST_P * 0xFFFF)的概率是多少呢？自然就是ZSKIPLIST_P，也就是0.25了。

         因此，最終返回level為1的概率是1-0.25=0.75，返回level為2的概率為0.25*0.75，返回level為3的概率為0.25*0.25*0.75......因此，如果返回level為k的概率為x，則返回level為k+1的概率為0.25*x，換句話說，如果k層的結點數是x，那麼k+1層就是0.25*x了。這就是所謂的冪次定律（powerlaw），越大的數出現的概率越小。

#include <stdio.h>
#include <math.h>
	
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */
#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */
	
int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

int main () {
 unsigned int trytimes = 0xffffff;
    unsigned int i = 0;
    int resset[33] = {trytimes,};
    double percent = 0.0;
    
    for(i = 0; i < trytimes; i++){
        resset[zslRandomLevel()]++;
    }
    
    for(i = 0; i <= 32; i++){
        if(resset[i] == 0){
            percent = 0.0;
        }
        else{
            percent = (double)resset[i]/resset[0];
        }   
        printf("resset[%u] is %d, percentage of resset[%u] is %f%%\n", 
            i, resset[i], i-1, percent);
    }
	return 0;
}

輸出結果：

resset[0] is 16777215, percentage of resset[4294967295] is 1.000000%
resset[1] is 12583714, percentage of resset[0] is 0.750048%
resset[2] is 3146005, percentage of resset[1] is 0.187517%
resset[3] is 785421, percentage of resset[2] is 0.046815%
resset[4] is 196516, percentage of resset[3] is 0.011713%
resset[5] is 49350, percentage of resset[4] is 0.002941%
resset[6] is 12163, percentage of resset[5] is 0.000725%
resset[7] is 3024, percentage of resset[6] is 0.000180%
resset[8] is 748, percentage of resset[7] is 0.000045%
resset[9] is 216, percentage of resset[8] is 0.000013%
resset[10] is 46, percentage of resset[9] is 0.000003%
resset[11] is 12, percentage of resset[10] is 0.000001%
resset[12] is 0, percentage of resset[11] is 0.000000%
resset[13] is 0, percentage of resset[12] is 0.000000%
resset[14] is 0, percentage of resset[13] is 0.000000%
resset[15] is 0, percentage of resset[14] is 0.000000%
resset[16] is 0, percentage of resset[15] is 0.000000%
resset[17] is 0, percentage of resset[16] is 0.000000%
resset[18] is 0, percentage of resset[17] is 0.000000%
resset[19] is 0, percentage of resset[18] is 0.000000%
resset[20] is 0, percentage of resset[19] is 0.000000%
resset[21] is 0, percentage of resset[20] is 0.000000%
resset[22] is 0, percentage of resset[21] is 0.000000%
resset[23] is 0, percentage of resset[22] is 0.000000%
resset[24] is 0, percentage of resset[23] is 0.000000%
resset[25] is 0, percentage of resset[24] is 0.000000%
resset[26] is 0, percentage of resset[25] is 0.000000%
resset[27] is 0, percentage of resset[26] is 0.000000%
resset[28] is 0, percentage of resset[27] is 0.000000%
resset[29] is 0, percentage of resset[28] is 0.000000%
resset[30] is 0, percentage of resset[29] is 0.000000%
resset[31] is 0, percentage of resset[30] is 0.000000%
resset[32] is 0, percentage of resset[31] is 0.000000%

這個測試就是做個較大的連結串列1677215；看下各層數分佈的情況。原來的用例是輸出各層的跟上一層。我改為都跟最底層的全量資料.對比。層數分佈基本上是符合預期的。最開始沒看到之前，打算用java 程式碼模擬下。C是真不會了。

3.2 插入

    跳錶插入通常分成三步，第一步找到插入位置插入，第二步根據隨機高度，確定是否重複前面的步驟。第三步去做插入節點前後指向的調整，redis跳錶因為比普通跳錶多了rank.所以看起來更復雜。看下程式碼：

/*
 * 建立一個成員為 obj ，分值為 score 的新節點，
 * 並將這個新節點插入到跳躍表 zsl 中。
 * 
 * 函式的返回值為新節點。
 *
 * T_wrost = O(N^2), T_avg = O(N log N)
 */
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    redisAssert(!isnan(score));

    // 在各個層查詢節點的插入位置
    // T_wrost = O(N^2), T_avg = O(N log N)
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        /* store rank that is crossed to reach the insert position */
        // 如果 i 不是 zsl->level-1 層
        // 那麼 i 層的起始 rank 值為 i+1 層的 rank 值
        // 各個層的 rank 值一層層累積
        // 最終 rank[0] 的值加一就是新節點的前置節點的排位
        // rank[0] 會在後面成為計算 span 值和 rank 值的基礎
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];

        // 沿著前進指標遍歷跳躍表
        // T_wrost = O(N^2), T_avg = O(N log N)
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比對分值
                (x->level[i].forward->score == score &&
                // 比對成員， T = O(N)
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) {

            // 記錄沿途跨越了多少個節點
            rank[i] += x->level[i].span;

            // 移動至下一指標
            x = x->level[i].forward;
        }
        // 記錄將要和新節點相連線的節點
        update[i] = x;
    }

    /* we assume the key is not already inside, since we allow duplicated
     * scores, and the re-insertion of score and redis object should never
     * happen since the caller of zslInsert() should test in the hash table
     * if the element is already inside or not. 
     *
     * zslInsert() 的呼叫者會確保同分值且同成員的元素不會出現，
     * 所以這裡不需要進一步進行檢查，可以直接建立新元素。
     */

    // 獲取一個隨機值作為新節點的層數
    // T = O(N)
    level = zslRandomLevel();

    // 如果新節點的層數比表中其他節點的層數都要大
    // 那麼初始化表頭節點中未使用的層，並將它們記錄到 update 陣列中
    // 將來也指向新節點
    if (level > zsl->level) {

        // 初始化未使用層
        // T = O(1)
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }

        // 更新表中節點最大層數
        zsl->level = level;
    }

    // 建立新節點
    x = zslCreateNode(level,score,obj);

    // 將前面記錄的指標指向新節點，並做相應的設定
    // T = O(1)
    for (i = 0; i < level; i++) {
        
        // 設定新節點的 forward 指標
        x->level[i].forward = update[i]->level[i].forward;
        
        // 將沿途記錄的各個節點的 forward 指標指向新節點
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        // 計算新節點跨越的節點數量
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

        // 更新新節點插入之後，沿途節點的 span 值
        // 其中的 +1 計算的是新節點
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    // 未接觸的節點的 span 值也需要增一，這些節點直接從表頭指向新節點
    // T = O(1)
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    // 設定新節點的後退指標
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;

    // 跳躍表的節點計數增一
    zsl->length++;

    return x;
}

有些長，分佈來看。

插入點（就是新插入結點在每層上的前驅結點）redis使用了一個數組來記錄，就是 zskiplistNode *update[ZSKIPLIST_MAXLEVEL], 外一個數組來記錄插入點前繼節點排名，所謂排名就是就連結串列中的位置，這個有什麼用呢？主要是用來更新span欄位    unsigned int rank[ZSKIPLIST_MAXLEVEL];

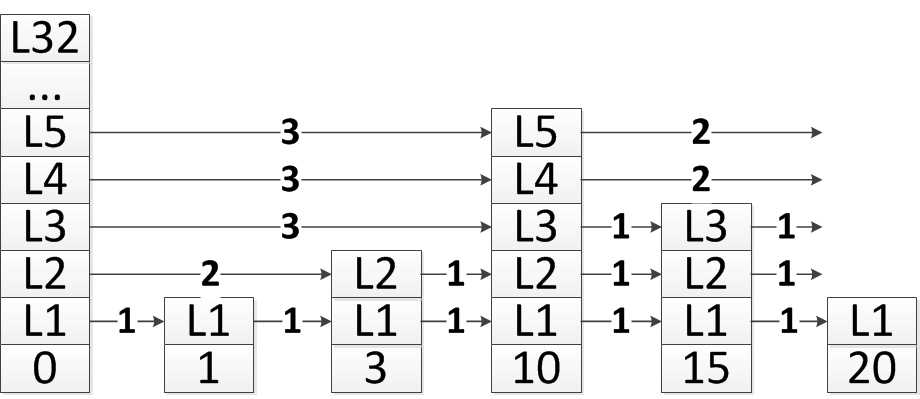
只看程式碼是抽象的，有個圖就好理解一下。下圖是一個簡化的跳躍表，每個結點只保留了分數、層指標和層跨度。所以，下圖中表頭結點排名為0，分數為1、3、10、15、20的結點，排名分別為1、2、3、4、5。

首先看插入程式碼的第一部分，也就是尋找插入結點在每層上的前驅結點的程式碼：

 x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }

   從表頭結點的最高層開始查詢，首先在該層中尋找插入結點的前驅結點。只要插入結點比當前結點x在該層的後繼結點x->level[i].forward要大，則首先記錄x後繼結點的排名：rank[i] += x->level[i].span; 接著開始比較x的後繼結點：x =x->level[i].forward。

        注意，因為Redis中的跳躍表中，允許分數重複而不允許成員物件重複。所以，這裡的判斷條件中，一旦分數相同，則要比較成員物件的字典順序。

        一旦當前結點x的後繼結點為空，或者後繼結點比插入結點要大，說明找到了插入結點在該層的前驅結點，記錄到update陣列中：update[i] = x，此時，rank[i]就是結點x的排名。

     然後，開始遍歷下一層，從x結點開始比較。

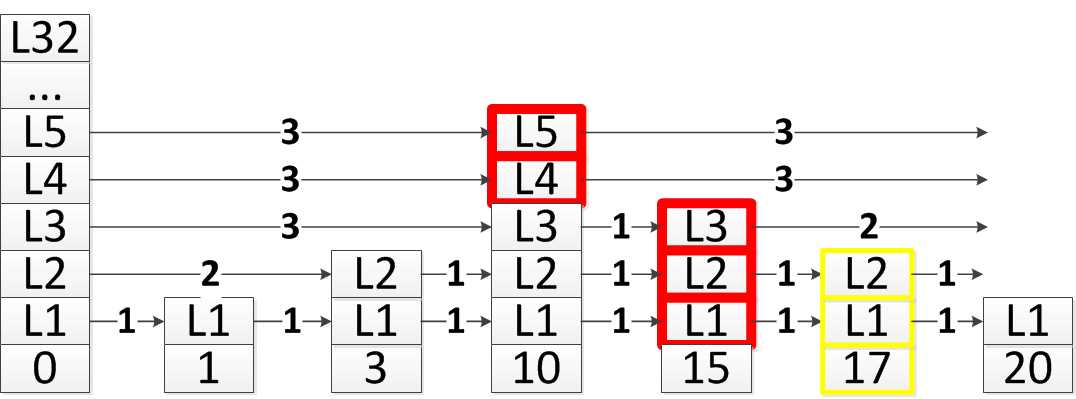
     在上圖的跳躍表中，假設現在要插入的結點分數為17，黃色虛線所標註的，就是插入新結點的位置。下面標註紅色的，就是在每層找到的插入結點的前驅結點，記錄在update[i]中，而rank[i]記錄了update[i]在跳躍表中的排名，因此，rank[4] = 3, rank[3] = 3, rank[2] = 4, rank[1] = 4, rank[0] = 4。這一點要理解，不然就容易有歧義，是前去節點的屬性。

接著就是將結點插入到跳躍表中。

 /* we assume the key is not already inside, since we allow duplicated
     * scores, and the re-insertion of score and redis object should never
     * happen since the caller of zslInsert() should test in the hash table
     * if the element is already inside or not. 
     *
     * zslInsert() 的呼叫者會確保同分值且同成員的元素不會出現，
     * 所以這裡不需要進一步進行檢查，可以直接建立新元素。
     */

    // 獲取一個隨機值作為新節點的層數
    // T = O(N)
    level = zslRandomLevel();

    // 如果新節點的層數比表中其他節點的層數都要大
    // 那麼初始化表頭節點中未使用的層，並將它們記錄到 update 陣列中
    // 將來也指向新節點
    if (level > zsl->level) {

        // 初始化未使用層
        // T = O(1)
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }

        // 更新表中節點最大層數
        zsl->level = level;
    }

註釋比較清晰了：首先利用zslRandomLevel，生成一個隨機的層數level。如果該level大於當前跳躍表的最大level的話，則需要初始化插入結點在超出層上，也就是在層數[zsl->level, level)上的前驅結點及其排名。這裡直接初始化前驅結點為頭結點，排名為0，並且初始化前驅結點在相應層上的層跨度為zsl->length，也就是頭結點和尾節點之間的距離。
  然後更新zsl->level的值。需要注意的是，因Redis中，使用雜湊表和跳躍表兩種結構表示有序集合，因此，在跳躍表的插入操作中，無需判斷插入結點是否與表中結點重複，這是因為在呼叫zslInsert之前，呼叫者應該已經使用雜湊表進行過檢測了。

接下來看第三步：

 // 建立新節點
    x = zslCreateNode(level,score,obj);

    // 將前面記錄的指標指向新節點，並做相應的設定
    // T = O(1)
    for (i = 0; i < level; i++) {
        
        // 設定新節點的 forward 指標
        x->level[i].forward = update[i]->level[i].forward;
        
        // 將沿途記錄的各個節點的 forward 指標指向新節點
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        // 計算新節點跨越的節點數量
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

        // 更新新節點插入之後，沿途節點的 span 值
        // 其中的 +1 計算的是新節點
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    // 未接觸的節點的 span 值也需要增一，這些節點直接從表頭指向新節點
    // T = O(1)
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

     首先呼叫zslCreateNode建立一個跳躍表節點。然後在層數[0, level)中，根據update[i]記錄的每層上的前驅結點，將新結點插入到每層中。

  插入新節點必然涉及到插入處前繼和後繼 節點指標的改，這個跟普通連結串列沒有什麼區別。至於span值的修改，需要理解下，節點的層跨度，等於該節點在第i層上的後繼節點的排名，減去該節點的排名。

新結點在第i層的後繼節點，也就是之前update[i]的後繼節點，它的排名是update[i]->level[i].span+ rank[i]，插入新結點之後，它的排名加1，也就是update[i]->level[i].span + rank[i] + 1。新結點的排名，就是rank[0]+ 1，因此，新結點在第i層的層跨度就是(update[i]->level[i].span + rank[i] + 1) – (rank[0] + 1)，也就是update[i]->level[i].span- (rank[0] - rank[i])

如果新結點層數level小於zsl->level，則在[level,zsl->level)中，所有找到的前驅結點的層跨度要加1.

因此，插入新結點17後，效果如下：

 // 設定新節點的後退指標
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;

    // 跳躍表的節點計數增一
    zsl->length++;

最後就是更新新結點x，及其後繼節點的前驅指標。並更新跳躍表的長度。

3.3刪除：

 刪除節點與插入節點類似，也是要先找到節點在刪除。相對簡單些。

/* Delete an element with matching score/object from the skiplist. 
 *
 * 從跳躍表 zsl 中刪除包含給定節點 score 並且帶有指定物件 obj 的節點。
 *
 * T_wrost = O(N^2), T_avg = O(N log N)
 */
int zslDelete(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    // 遍歷跳躍表，查詢目標節點，並記錄所有沿途節點
    // T_wrost = O(N^2), T_avg = O(N log N)
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        // 遍歷跳躍表的複雜度為 T_wrost = O(N), T_avg = O(log N)
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比對分值
                (x->level[i].forward->score == score &&
                // 比對物件，T = O(N)
                compareStringObjects(x->level[i].forward->obj,obj) < 0)))

            // 沿著前進指標移動
            x = x->level[i].forward;

        // 記錄沿途節點
        update[i] = x;
    }

    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. 
     *
     * 檢查詢到的元素 x ，只有在它的分值和物件都相同時，才將它刪除。
     */
    x = x->level[0].forward;
    if (x && score == x->score && equalStringObjects(x->obj,obj)) {
        // T = O(1)
        zslDeleteNode(zsl, x, update);
        // T = O(1)
        zslFreeNode(x);
        return 1;
    } else {
        return 0; /* not found */
    }

    return 0; /* not found */
}

/* Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank 
 * 
 * 內部刪除函式，
 * 被 zslDelete 、 zslDeleteRangeByScore 和 zslDeleteByRank 等函式呼叫。
 *
 * T = O(1)
 */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;

    // 更新所有和被刪除節點 x 有關的節點的指標，解除它們之間的關係
    // T = O(1)
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {//待刪除節點沒有出現在此層--跨度減1即可
            update[i]->level[i].span -= 1;
        }
    }

    // 更新被刪除節點 x 的前進和後退指標
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }

    // 更新跳躍表最大層數（只在被刪除節點是跳躍表中最高的節點時才執行）
    // T = O(1)
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;

    // 跳躍表節點計數器減一
    zsl->length--;
}

/* Delete all the elements with rank between start and end from the skiplist.
 *
 * 從跳躍表中刪除所有給定排位內的節點。
 *
 * Start and end are inclusive. Note that start and end need to be 1-based 
 *
 * start 和 end 兩個位置都是包含在內的。注意它們都是以 1 為起始值。
 *
 * 函式的返回值為被刪除節點的數量。
 *
 * T = O(N)
 */
unsigned long zslDeleteRangeByRank(zskiplist *zsl, unsigned int start, unsigned int end, dict *dict) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long traversed = 0, removed = 0;
    int i;
    // 沿著前進指標移動到指定排位的起始位置，並記錄所有沿途指標
    x = zsl->header;
    //尋找待更新的節點
    for (i = zsl->level-1; i >= 0; i--) {
        //指標前移的必要條件是前繼指標不為空
        while (x->level[i].forward && (traversed + x->level[i].span) < start) {
            //排名累加
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
 
    //下面的節點排名肯定大於等於start
    traversed++;
    x = x->level[0].forward;
    while (x && traversed <= end) {
        //逐個刪除後繼節點,直到end為止
        zskiplistNode *next = x->level[0].forward;
        zslDeleteNode(zsl,x,update); //刪除節點
        dictDelete(dict,x->obj);  //字典刪除
        zslFreeNode(x); //釋放節點
        removed++;
        //每刪除一個節點,排名加1
        traversed++;
        x = next;
    }
    return removed;
}

查詢

跳躍表提供了根據排名查詢元素，以及根據分數或群排名的API，間接提供了根據分數獲取元素的API，查詢體現了跳躍表的優勢，但實現相對簡單，主要是判斷在當前層比對的元素是否是否小於給定元素，如果小於，且其後繼指標不為空，則繼續往前查詢（這效率是很高的），否則往下一層找（效率相對低一點）：
 

/* Find the rank for an element by both score and key.
 *
 * 查詢包含給定分值和成員物件的節點在跳躍表中的排位。
 *
 * Returns 0 when the element cannot be found, rank otherwise.
 *
 * 如果沒有包含給定分值和成員物件的節點，返回 0 ，否則返回排位。
 *
 * Note that the rank is 1-based due to the span of zsl->header to the
 * first element. 
 *
 * 注意，因為跳躍表的表頭也被計算在內，所以返回的排位以 1 為起始值。
 *
 * T_wrost = O(N), T_avg = O(log N)
 */
unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    // 遍歷整個跳躍表
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        // 遍歷節點並對比元素
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比對分值
                (x->level[i].forward->score == score &&
                // 比對成員物件
                compareStringObjects(x->level[i].forward->obj,o) <= 0))) {

            // 累積跨越的節點數量
            rank += x->level[i].span;

            // 沿著前進指標遍歷跳躍表
            x = x->level[i].forward;
        }

        /* x might be equal to zsl->header, so test if obj is non-NULL */
        // 必須確保不僅分值相等，而且成員物件也要相等
        // T = O(N)
        if (x->obj && equalStringObjects(x->obj,o)) {
            return rank;
        }
    }

    // 沒找到
    return 0;
}
/* Finds an element by its rank. The rank argument needs to be 1-based. 
 * 
 * 根據排位在跳躍表中查詢元素。排位的起始值為 1 。
 *
 * 成功查詢返回相應的跳躍表節點，沒找到則返回 NULL 。
 *
 * T_wrost = O(N), T_avg = O(log N)
 */
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
    zskiplistNode *x;
    unsigned long traversed = 0;
    int i;

    // T_wrost = O(N), T_avg = O(log N)
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        // 遍歷跳躍表並累積越過的節點數量
        while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
        {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }

        // 如果越過的節點數量已經等於 rank
        // 那麼說明已經到達要找的節點
        if (traversed == rank) {
            return x;
        }

    }

    // 沒找到目標節點
    return NULL;
}

其它的待整理吧。

總結：

 看書吧，這一章介紹的比較少。只介紹下結構，更靠畫圖來解釋下，對於原始碼的實現沒有怎麼介紹。網上還是有很多資源可以補充來看的。單看redis的跳錶結構，多了rank便利查詢,但是對應的複雜度就多了。

參考 ：

https://blog.csdn.net/idwtwt/article/details/80233859