1 子帶劃分濾波器 SplitFilter

1.1 全通濾波器 AllPassFilter

從函式中
tmp32 = state32 + filter_coefficient * *data_in;
state32 = (*data_in * (1 << 14)) - filter_coefficient * tmp16;
令$x(n)$為輸入序列，$y(n)$為輸出序列，$c$為實係數filter_coefficient ，可知表示 :
$y(n) =x(n-1)-c*y(n-1) + c*x(n)$

1.2 IIR 傳輸函式的並聯全通實現

根據IIR傳輸函式通過全通函式並聯性質【參考文獻《數字訊號處理–基於計算機的方法》】：

• 一對互補的低通和高通傳輸函式可有兩個穩定的全通濾波器並聯組成：
  $F(z)= \frac{1}{2}(A_0(z)+A_1(z))$$G(z)= \frac{1}{2}(A_0(z)-A_1(z))$$|F(z)|^2 + |G(z)|^2 = 1$

• 對於低通高通濾波器對，傳輸函式的階數N必須是奇數，其中$A_0(z)$和$A_1(z)$的階數相差1。

由上述可知，一對互補的低通高通傳輸函式可以有兩個相同階數的全通函式多相分解得出：
$E(z) = E_0(z^2) + z^{-1}E_1(z^2)$
$E_0(z^2)$和$E_1(z^2)$為相同階數的全通函式，$z^{-1}$使輸入序列移位。

webrtc vad 中SplitFilter 正是通過上述IIR傳輸函式多相分解成全通函式並聯技術實現，並實現對輸出2倍下抽樣。

第一個全通濾波器的引數kAllPassCoefsQ15[0] = 20972, 即$c=20972/(2^{15})=0.64$，則傳輸函式：
$A_0(z) = \frac{0.64+z^{-2}}{1+0.64*z^{-2}}$
第二個全通濾波器的引數kAllPassCoefsQ15[0] = 5571, 即$c=5571/(2^{15})=0.17$， 則傳輸函式：
$A_1(z) = \frac{0.17+z^{-2}}{1+0.17*z^{-2}}$
第一個全通濾波器的輸入序列data_in[n]是第二個全通函式輸入序列data_in[n+1]的移位，且全通濾波器中輸出是 tmp16 = (int16_t) (tmp32 >> 16); // Q(-1) *data_out++ = tmp16;Q(-1), 即$1/2$的輸出，則傳輸函式為
$H(z)= \frac{1}{2}(A_1(z) _-^+ z^{-1}A_0(z))$

由於全通函式的輸出只與當前輸入值和歷史第二輸入值、輸出值有關,而全通濾波器輸入是2倍下抽樣輸入x(2n+1)，即data_in[1]、data_in[3]、data_in[5]……，則輸出也只計算得到data_out[1]、data_out[3]、data_out[5]……, 相當於對原輸出y(n)進行2倍下抽樣的資料y(2n+1)。

函式中*hp_data_out++ -= *lp_data_out;對應的高通傳輸函式：
$H_{high} =\frac{1}{2}(A_1(z) - z^{-1}A_0(z))$$H_{high} =\frac{1}{2}( \frac{0.17+z^{-2}}{1+0.17*z^{-2}} - z^{-1}\frac{0.64+z^{-2}}{1+0.64*z^{-2}})$
函式中*lp_data_out++ += tmp_out;對應的低通傳輸函式：
$H_{low} =\frac{1}{2}(A_1(z) + z^{-1}A_0(z))$$H_{low} =\frac{1}{2}( \frac{0.17+z^{-2}}{1+0.17*z^{-2}} + z^{-1}\frac{0.64+z^{-2}}{1+0.64*z^{-2}})$

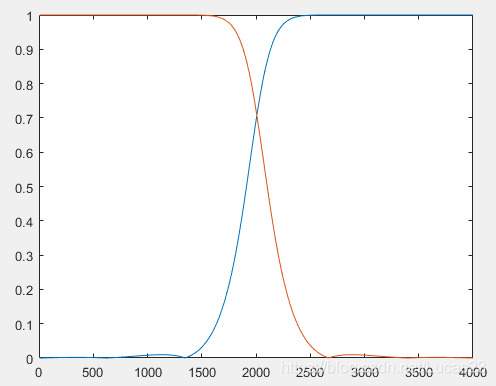
通過matlab畫出上述低通濾波器和高通濾波器：

%sliptfilter

clc; close all; clear all;
%20972 5571
% 全通濾波器 z^-1* A1(z)
c = 20972/(2^15);
B =[0 c 0 1];
A =[1 0 c];
[A1,W1] = freqz(B,A,1024,'whole',4000);
A1f =abs(A1);
A1a = angle(A1);
x = 4000/512;
%plot((1:512)*x,A1f(1:512));

% 全通濾波器  A0(z)
c = 5571/(2^15);
B =[c 0 1];
A =[1 0 c];
[A0,W0] = freqz(B,A,1024,'whole',4000);
A0f =abs(A0);
A0a = angle(A0);
%plot((1:512)*x,A0f(1:512));

% 高通濾波
H = A1 - A0;
H = H/2;
Hf=abs(H);
Ha= angle(H);
plot((1:512)*x,Hf(1:512)); hold on;
%低通濾波
L = A1 + A0;
L = L/2;
Lf = abs(L);
La = angle(L);
plot((1:512)*x,Lf(1:512));