最近總是遇到主題模型LDA（Latent Dirichlet Allocation），網上的部落格寫的天花亂墜而不知所以然，無奈看了最厚的《LDA數學八卦》，觀完略通一二，記錄於此~順便放兩張遇到的圖，挺有意思的，共勉吧：

主題模型

首先我們來看什麼叫主題模型~我們來考慮一個問題：判斷文字相關程度。怎麼判斷呢？是看相同詞語出現的次數來判斷嗎（TF-IDF）？顯然這太草率了。從內容角度來講，只要兩篇文章的主題是相同的，這兩篇文章就是相關的。比如一片文章介紹的是京東618，另一片是天貓雙11，主題基本相同。
我們來看看生成一篇文章有怎麼的手段：

Unigram Model

假設我們的詞典一共有V個詞v

1,v2,...,vV,那麼最簡單的主題模型就是認為上帝（你！就！是！上！帝！┗|｀O′|┛ ）是按照如下的遊戲規則產生文字的：

※※※※※※※※※
Unigram Model
※※※※※※※※※
1.上帝只有一個骰（tou，有文化真可怕）子，這個骰子有V個面，每個面對應一個詞，各個面的概率不一；
2。每拋一次骰子，丟擲的面就對應的產生一個詞；如果一片文件中有n個詞，上帝就是獨立的拋n次骰子產生這n個詞。

PLSA

這個就是一個主題模型啦~Hoffman認為上帝是按照如下規則生成文字：

※※※※※※※※※※
PLSA Topic Model
※※※※※※※※※※
1. 上帝有兩種型別的骰子，一類是doc-topic骰子，每個doc-topic骰子有K個面，每個面都是一個topic的編號；一類是topic-word骰子，每個topic-word骰子有V個面，每個面對應一個詞；

2. 上帝一共有K個topic-word骰子，每個有一個編號，編號1到K
3. 生成每篇文件之前，上帝都先為這篇文章製造一個特定的doc-topic骰子，然後重複如下的文件詞語生成過程:

• 投擲這個doc-topic骰子，得到一個topic編號z
• 選擇編號為z的topic-word骰子，投擲這個骰子得到一個詞

貝葉斯學派

如果沒有貝葉斯學派，大家都是頻率主義學派，我們的這篇博文到此就差不多該結束了。我們看看貝葉斯學派有什麼高見，作了什麼補充吧。先簡要的看看兩個學派有什麼區別：

頻率主義學派

萬物皆可頻。每個事件都有個確定的概率，我們可以通過做實驗得到頻率，再用這個頻率去估計概率。比如，扔硬幣，正面向上一定是有個概率的。我們扔了5000次，有2000次正面向上，3000次背面向上，這這個概率就是2/3（頻率主義內心OS：我不聽我不聽，我都做了5000次試驗了，你還想怎樣(；′⌒`)）。

貝葉斯學派

你做5萬次也沒有用。。。2/3也許只是一個概率分佈的極值罷了。沒有絕對的概率值等著我們去接近，但是我們可以學概率分佈：比如令正面向上的概率是高斯分佈，然後做實驗得到均值（2/3）方差什麼的。

共軛

本文就提到兩個共軛Beta-Binomial共軛和Dirichlet-Multinomial共軛
關於Beta-Binomial共軛，轉一個不錯的解讀：

舉一個簡單的例子，熟悉棒球運動的都知道有一個指標就是棒球擊球率(batting average)，就是用一個運動員擊中的球數除以擊球的總數，我們一般認為0.266是正常水平的擊球率，而如果擊球率高達0.3就被認為是非常優秀的。

現在有一個棒球運動員，我們希望能夠預測他在這一賽季中的棒球擊球率是多少。你可能就會直接計算棒球擊球率，用擊中的數除以擊球數，但是如果這個棒球運動員只打了一次，而且還命中了，那麼他就擊球率就是100%了，這顯然是不合理的，因為根據棒球的歷史資訊，我們知道這個擊球率應該是0.215到0.36之間才對啊。

對於這個問題，我們可以用一個二項分佈表示（一系列成功或失敗），一個最好的方法來表示這些經驗（在統計中稱為先驗資訊）就是用beta分佈，這表示在我們沒有看到這個運動員打球之前，我們就有了一個大概的範圍。beta分佈的定義域是(0,1)這就跟概率的範圍是一樣的。

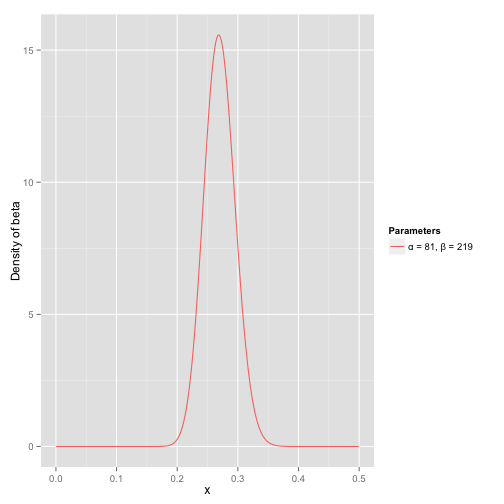
接下來我們將這些先驗資訊轉換為beta分佈的引數，我們知道一個擊球率應該是平均0.27左右，而他的範圍是0.21到0.35，那麼根據這個資訊，我們可以取α=81,β=219

之所以取這兩個引數是因為：

beta分佈的均值是α/(α+β)=81/(81+219)=0.27
從圖中可以看到這個分佈主要落在了(0.2,0.35)間，這是從經驗中得出的合理的範圍。
在這個例子裡，我們的x軸就表示各個擊球率的取值，x對應的y值就是這個擊球率所對應的概率。也就是說beta分佈可以看作一個概率的概率分佈。

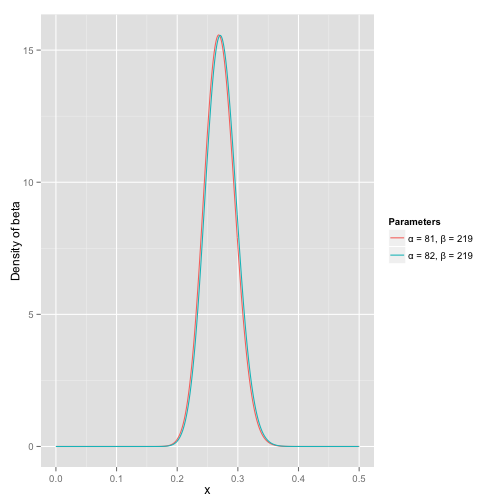
那麼有了先驗資訊後，現在我們考慮一個運動員只打一次球，那麼他現在的資料就是”1中;1擊”。這時候我們就可以更新我們的分佈了，讓這個曲線做一些移動去適應我們的新資訊。beta分佈在數學上就給我們提供了這一性質，他與二項分佈是共軛先驗的（Conjugate_prior）。所謂共軛先驗就是先驗分佈是beta分佈，而後驗分佈同樣是beta分佈。結果很簡單：

Beta(α0+hits,β0+misses)

其中α0和β0是一開始的引數，在這裡是81和219。所以在這一例子裡，α增加了1(擊中了一次)。β沒有增加(沒有漏球)。這就是我們的新的beta分佈Beta(81+1,219)，我們跟原來的比較一下：

可以看到這個分佈其實沒多大變化，這是因為只打了1次球並不能說明什麼問題。但是如果我們得到了更多的資料，假設一共打了300次，其中擊中了100次，200次沒擊中，那麼這一新分佈就是：

beta(81+100,219+200)

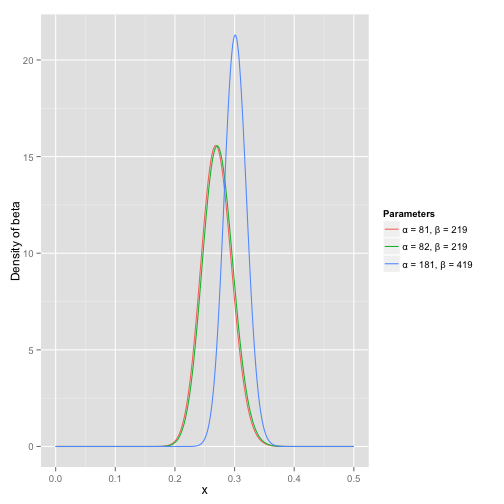
注意到這個曲線變得更加尖，並且平移到了一個右邊的位置，表示比平均水平要高。
一個有趣的事情是，根據這個新的beta分佈，我們可以得出他的數學期望為：α/(α+β)=(82+100)/(82+100+219+200)=.303 ，這一結果要比直接的估計要小 100/(100+200)=.333 。你可能已經意識到，我們事實上就是在這個運動員在擊球之前可以理解為他已經成功了81次，失敗了219次這樣一個先驗資訊。

因此，對於一個我們不知道概率是什麼，而又有一些合理的猜測時，beta分佈能很好的作為一個表示概率的概率分佈。
OK.從出你多少能感受到那麼點意思：先驗分佈確實有些道理。
在貝葉斯體系中

先驗分布+數據知識=後驗分布
在上述的例子中有：
Beta(p|α,β)+Binom(m1,m2)=Beta(p|α+m1,β+m2)
我們注意到這裡先驗分佈和後驗分佈相同，滿足這樣的結構的分佈我們叫：Beta-Binomial共軛。還有一組共軛Dirichlet-Multinomial共軛我們就知道個所以然啦~

LDA

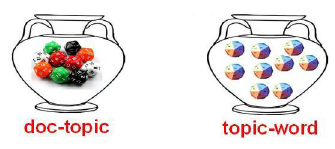
終於迎來LDA模型。其實就是給PLSA主題模型加了貝葉斯先驗。注意到PLSA中上帝擲document-topic骰子之前先現場做一個骰子的，進行整個語料庫的實驗時也是現場做k個topic-word骰子的。怎麼能現場製作呢！貝葉斯ist憤怒了，應該是早就做好了現場拿才對！所以假設上帝有兩個大罈子一個裝滿document-topic骰子，另一個裝滿topic-word骰子。做實驗時現場抽取，而不是製作。而這個罈子裡骰子的分佈就是先驗。既然是骰子，所以分散式多項分佈，先驗最好就是取Dirichlet分佈啦~

LDA的主題模型結構如下：

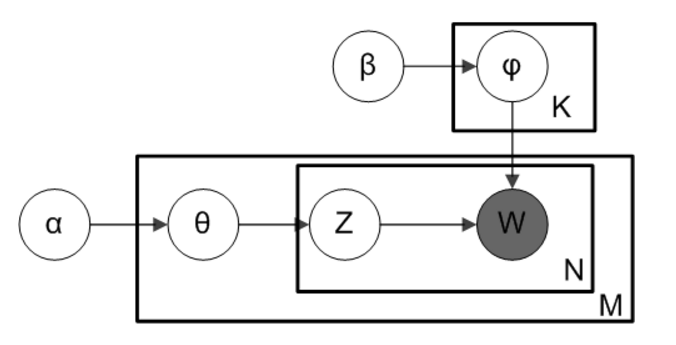
其中α,β是Dirichlet引數。