常見的策略有三種：

• 先進先出策略 FIFO（First In，First Out）
• 最少使用策略 LFU（Least Frequently Used）
• 最近最少使用策略 LRU（Least Recently Used）

對比陣列和連結串列：

• 陣列：是一塊連續的儲存單元
• 連結串列：是通過“指標”將一組零散的記憶體塊串聯起來進行儲存

三種常見的連結串列：

• 單鏈表
• 雙向連結串列
• 迴圈連結串列

下面說一下概念：

• 節點：記憶體塊
• 後繼指標 next：記錄下個結點地址的指標

   

說了這多，下面就開始說一下常見的三種連結串列

一、單鏈表

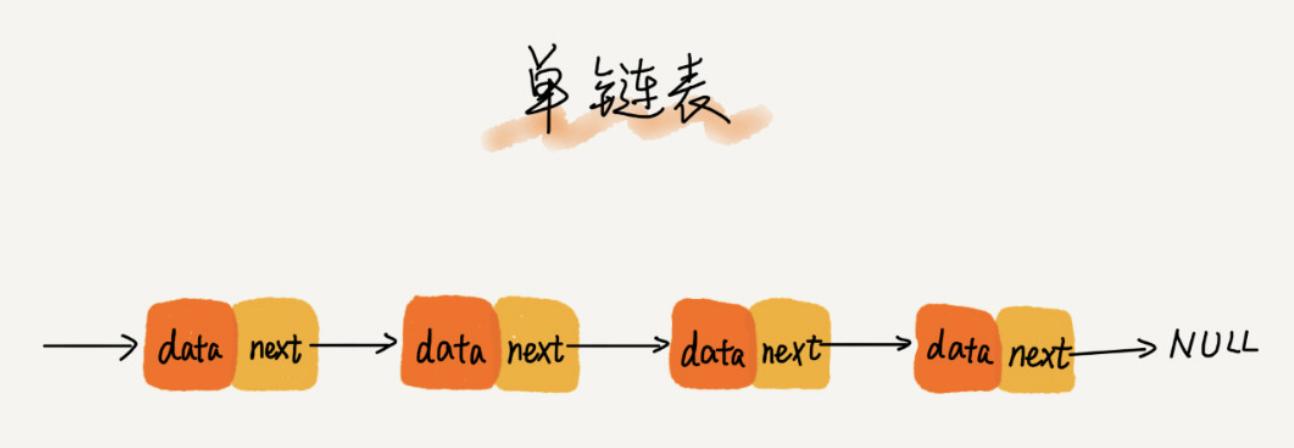
我們習慣性地把第一個結點叫作頭結點，把最後一個結點叫作尾結點。頭節點用來記錄連結串列的基地址，尾節點指向NULL，表示這是連結串列上的最後一個節點。

與陣列一樣，連結串列也支援資料的查詢、插入、刪除操作。

在進行陣列的插入、刪除操作時，為了保持記憶體資料的連續性，需要做大量的資料搬移，所以時間複雜度是 O(n)。而在連結串列中插入或者刪除一個數據，我們並不需要為了保持記憶體的連續性而搬移結點，因為連結串列的儲存空間本身就不是連續的。所以，在連結串列中插入和刪除一個數據是非常快速的。

下圖為連結串列的插入、刪除操作，只需要考慮相鄰結點的指標改變，所以對應的時間複雜度是 O(1）：

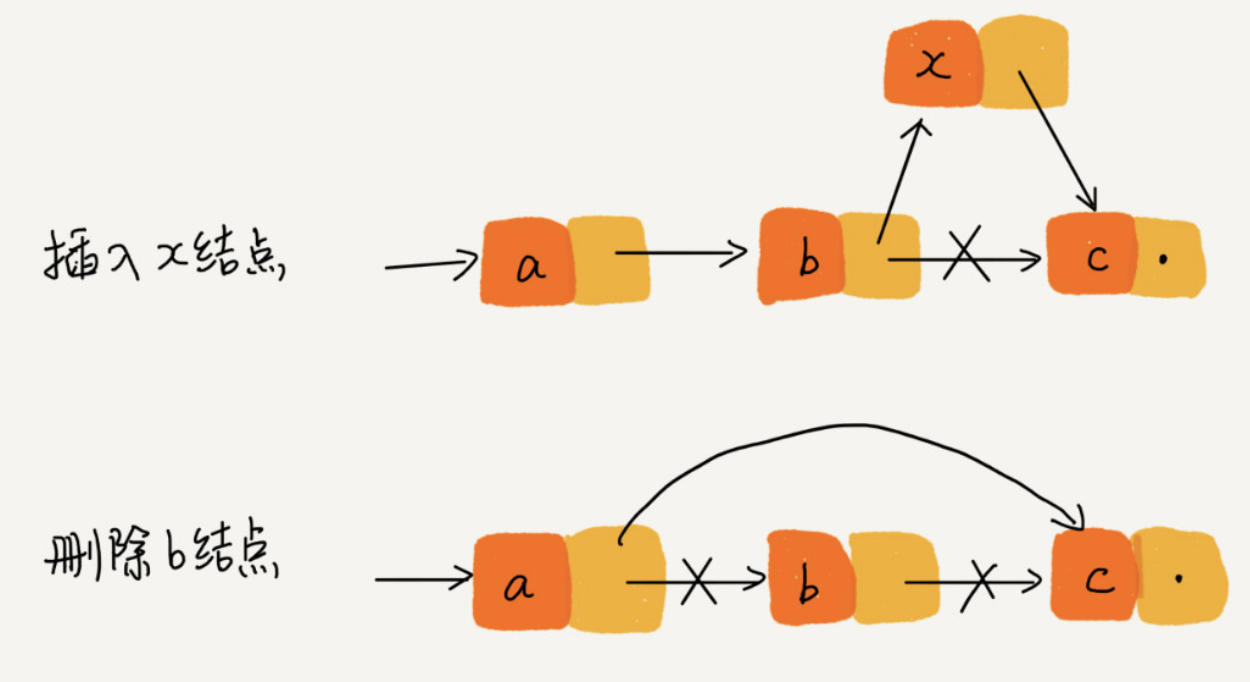
而相對插入刪除，連結串列的查詢就沒有陣列方便了，因為連結串列的資料不是連續儲存的，因此在查詢的時候就不會想陣列那樣通過下標來直接訪問，連結串列需要通過遍歷來查詢，因此，連結串列的查詢時間複雜度為O(n)。

二、迴圈連結串列

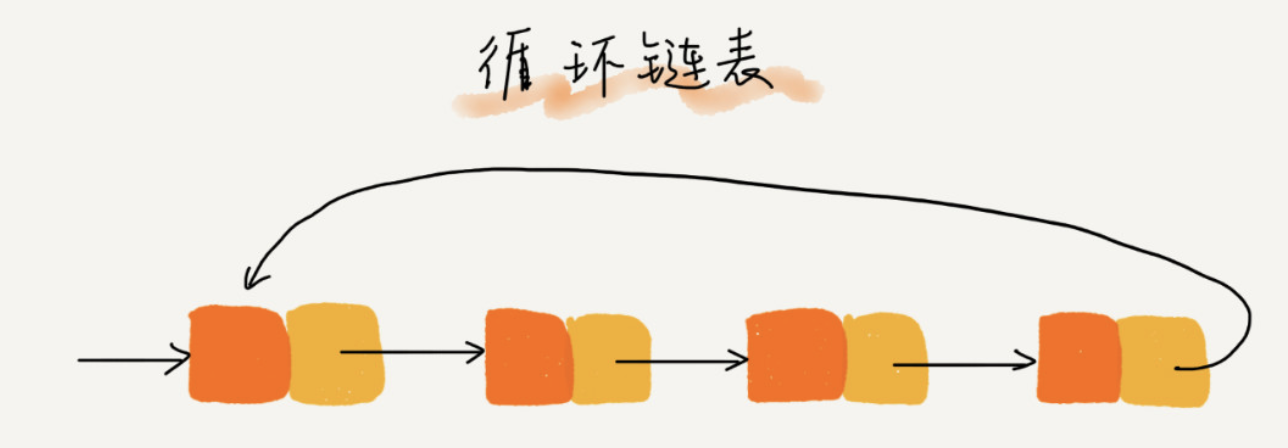
迴圈連結串列是特殊的單鏈表

跟單鏈表唯一的區別就在尾結點。單鏈表的尾結點指標指向空地址。迴圈連結串列的尾結點指標是指向連結串列的頭結點。像一個環一樣首尾相連，所以叫作“迴圈”連結串列。

當要處理的資料具有環型結構特點時，就特別適合採用迴圈連結串列。比如著名的約瑟夫問題。

三、迴圈連結串列 

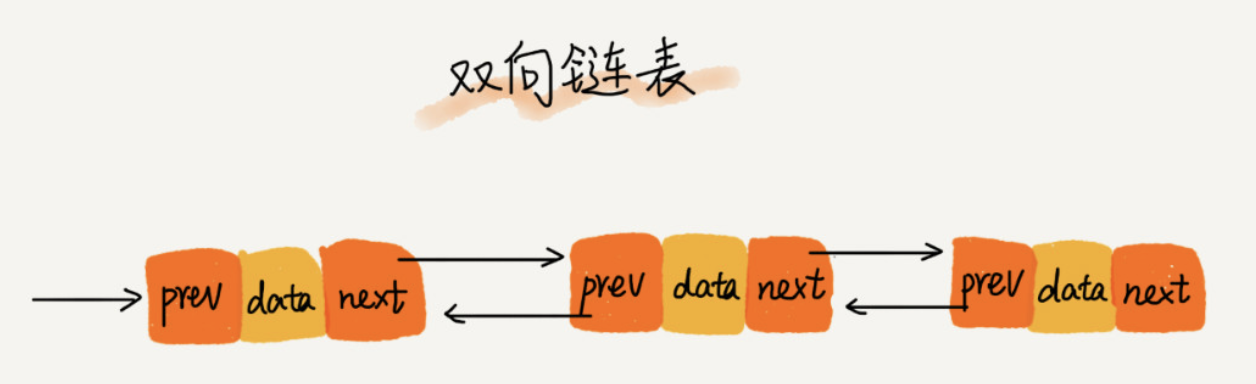
從圖中可以看出，雙向連結串列就是連結串列不止有後繼指標，還有一個前驅指標

 從結構上來看，雙向連結串列可以支援 O(1) 時間複雜度的情況下找到前驅結點，正是這樣的特點，也使雙向連結串列在某些情況下的插入、刪除等操作都要比單鏈表簡單、高效。