凌晨一點半的深圳雨夜：

豪雨當夜驚起有人賞，笑嘆落花無聲空飄零。
喜歡這種豪雨，讓人興奮。驚起作文以嗚呼之感嘆！

引用上一篇文章：
優化多核CPU的TCP新建連線效能–重排spinlock：https://blog.csdn.net/dog250/article/details/80575731
在這篇文章中，我將一個spinlock拆解成了per cpu的，然而並沒有提及spinlock本身的效能和可伸縮性(scalable)，那麼本文就來說一下。

一點說明

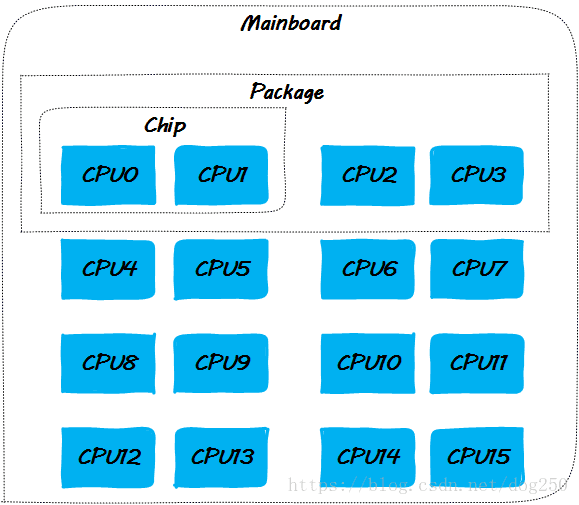
正文開始之前，先給出本文討論的各個場景基於的CPU佈局圖，本文中我們將描述很多的場景實驗，因為是分析原理，我將其定義為思想實驗

，假設我們思想實驗的系統擁有16核CPU，其中每一個CPU封裝有2個物理核，每一個物理核有兩個有獨立cache的核心，其佈局如下：

由於實現的可擴充套件性的原因，當前的大多數平臺在實現CPU cache一致性協議時有兩個選擇，一個是snoopy，一個是點對點unicast。

• snoopy方式
  這意味著cache一致性訊息通過匯流排廣播，於是就要偵聽匯流排以在某個時機獲得控制權。這種方式及其不易擴充套件，在CPU數目達到一定量時，匯流排的爭搶會很嚴重。
  參考乙太網的CSMA/CD協議，會得出一樣的結論，正如CSMA/CD的基於匯流排的乙太網由於其不可擴充套件性進化到了交換式乙太網一樣，CPU間的cache一致性協議的點對點unicast實現方式最終替代了snoopy(小規模本地cache一致性依然會採用snoopy的方式
  )。總而言之，是匯流排頻寬限制了snoopy想大規模SMP發展。
• 點對點unicast方式
  既然snoopy需要嚴格的匯流排仲裁，採用點對點的方式進行cache一致性的訊息路由就成了一個可選的應對措施，但是對於多個目的地的訊息的傳送方而言，one by one的按序in turn方式傳送就成了唯一的選擇，正是這種處理方式成了點對點unicast方式的另一個不可擴充套件性根源。
  但這種不可擴充套件性是針對更上層而言，在cache一致性協議的實現上，它克服了匯流排仲裁帶來的本層的不可擴充套件性。業界很多的場景都遵循了類似的匯流排–>點對點的發展軌跡，除了乙太網之外，還有PCI到PCIe的進化。無論哪種實現方式，其過程都體現了採用被動的NAK仲裁向主動的訊息路由方向的進化之路似乎是一條放之四海而皆準的康莊大道
  。

理解這些，特別是理解點對點unicast方式的one by one處理時延會隨著CPU核數的增加而線性增加為後面的內容埋下了伏筆。

在Linux核心中，先後有過新舊兩種版本的自旋鎖被大規模使用，一個是willd spinlock，另一個則是當前核心預設使用的ticket spinlock，下面的章節會簡而述之。

好了，正文開始！

wild spinlock

這種自旋鎖非常簡單，簡而言之就是一個整數：

typedef struct {
    volatile unsigned int lock;
} spinlock_t;

然後其加鎖和解鎖過程為：

void spin_lock(spinlock_t *lock)
{
    while (lock->lock == 1)
        ; // 自旋等待
}
void spin_unlock(spinlock_t *lock)
{
    lock->lock = 0;
}

然而在這種簡單的背後卻掩蓋著一個血雨腥風的戰場，我們看一下why。

根據上面的CPU佈局圖，我們可以瞭解到CPU之間的親密關係是不同的，特定CPU的cache line更新同步到不同CPU的cache line的時間也不同，這就意味著等待自旋鎖的CPU中哪個CPU先感知到lock->lock的變化，哪個就能優先獲得鎖。

這將大大有損等鎖者之間的公平性。這就好比一群人不排隊上火車，體格好的總是優先登車一樣。

為了解決這個公平性問題，ticket spinlock登場了。

ticket spinlock登場

ticket spinlock在設計上增加了一個等鎖期間單調遞增的ticket欄位(當然，在實現上如何體現這個ticket就是trick了)，確保了先到者先獲得鎖，從而保證了公平性。

Linux ticket spinlock的實現和執行過程

我先給出Linux ticket spinlock的虛擬碼實現，為了討論簡單，以下的程式碼中所有的自加(i++)操作均為原子操作，避免鎖中鎖。

• 定義spinlock

struct spinlock_t {
    // 上鎖者自己的排隊號
    int my_ticket;
    // 當前叫號
    int curr_ticket;
}

非常簡單，一個標準的排隊裝置，類似銀行叫號系統，每個辦理業務的取一個號，然後按照號碼的大小依次序列被服務。

• spin_lock上鎖

void spin_lock(spinlock_t *lock)
{
    int my_ticket;
    // 順位拿到自己的ticket號碼；
    my_ticket = lock->my_ticket++;
    while (my_ticket != lock->curr_ticket)
        ; // 自旋等待！
}

• spin_unlock解鎖

void spin_unlock(spinlock_t *lock)
{
    // 呼叫下一位！
    lock->curr_ticket++;
}

以上基本就是Linux ticket spinlock實現的全部了，沒什麼複雜的，沒什麼大不了的。如果說僅僅是為了讀懂程式碼，確實沒有什麼大不了的，然而深究起來卻可以發現它的不妙。

以下我就從cache的角度來分析一下這個自旋鎖的執行過程，以下面的程式碼片段為例：

void demo()
{
    spin_lock(&g_lock);
    g_var1 ++;
    g_var2 --;
    g_var3 = g_var1 + g_var2;
    spin_unlock(&g_lock)
}

依然是按步驟來。好了，開始我們的步驟。

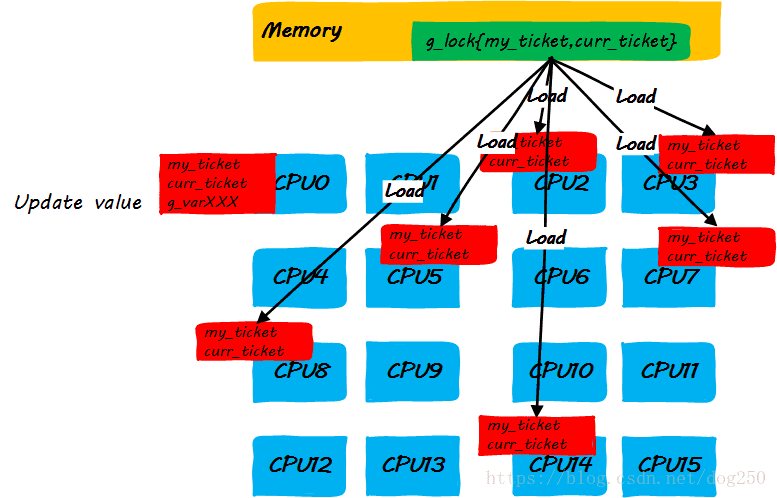
• step 1：CPU0申請鎖，獲取本地ticket到申請者的CPU cache
  
• step 2：執行鎖定區域指令的同時，其它CPU企圖獲取鎖而自旋
  
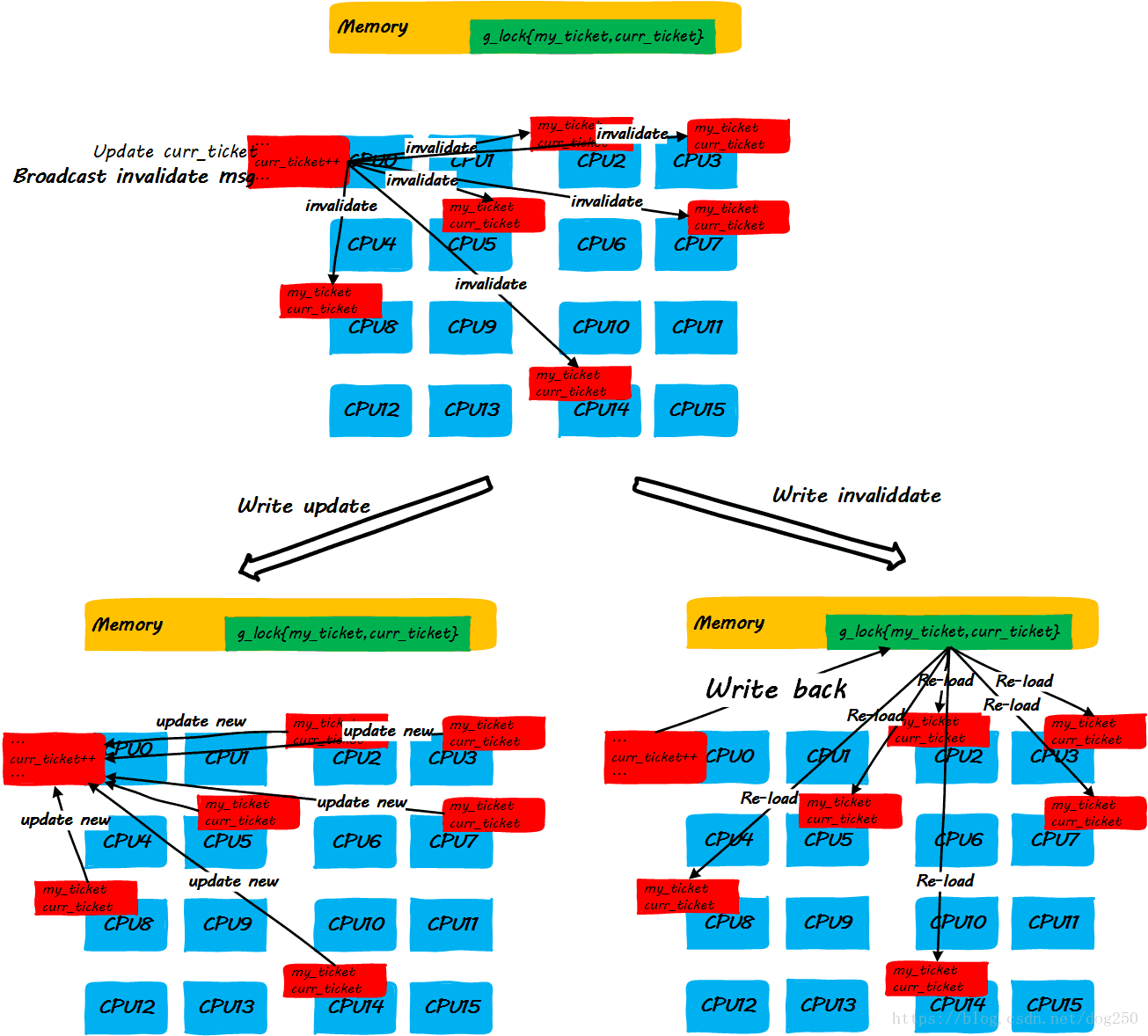
• step 3：CPU0釋放鎖
  

我們發現，上述的step3中的步驟有點太複雜了。當前的大多數平臺傾向於用點對點unicast的方式來更新cache line(因為broadcast方式對匯流排頻寬有要求，隨著CPU核數的增加，實現複雜度會增加，這是另一種不可伸縮！)，因此step3中更新每一個CPU cache line是一個one by one的過程，如果是write invalidate方式，就更會多出超級多的訪存指令，這些對於理解Linux ticket spinlock的不可伸縮性至關重要！

很顯然，隨著CPU核數的增加，隨著spinlock申請者的增加，step3中動作的執行時間會線性增加，最終，當spinlock的申請者達到一定數量時，多核CPU非但沒有提高效能，反而由於cache line更新的時間過久，反過來損害效能。

注意，wild spinlock同樣存在這個問題，wild spinlock背後的cache一致性過程和ticket spinlock完全一致，只是ticket spinlock嚴格限定了誰將下一個獲得鎖而wild spinlock並不能。

我們已經定性地描述了Linux ticket spinlock的當前實現會有什麼問題，為了定量地衡量這種實現會帶來哪些具體的後果，我需要簡單說一下Linux ticket spinlock(此後簡稱Linux spinlock)經典的Markov chain模型，請看下節。

Linux spinlock的馬爾科夫鏈模型

為了闡釋Linux spinlock的具體效能表現和帶來的結果，必然需要建立一個模型，本節我就說一下Linux spinlock的Markov chain模型，該模型結合排隊論可以精確描述和預測Linux spinlock的行為。

先看一下圖示：

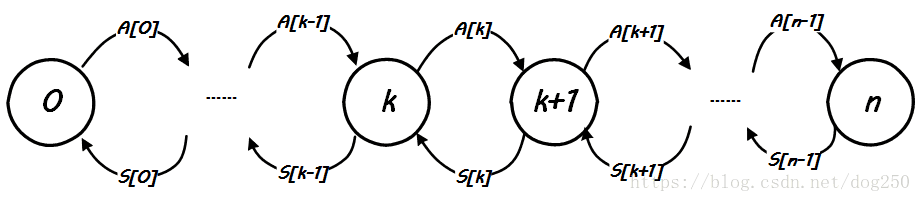
解釋一下：

這是一個Markov chain，其中一共有0$0$,1$1$,…n$n$一共n+1$n+1$個狀態，每一個狀態k$k$，表示系統中有k$k$個CPU正在自旋等待鎖，A[k]$A[k]$表示狀態k$k$轉換到狀態k+1$k+1$的速率，也就是相當於請求鎖的速率，而S[k]$S[k]$則表示狀態k+1$k+1$轉換到狀態k$k$的速率，也就是相當於釋放鎖的速率。

簡化起見，我們忽略掉spinlock到達的細節，即設在單一CPU核心上spinlock的請求達平均間隔為Tarrive$T_{arrive}$(事實上應該是指數分佈)，那麼單一CPU核心的spinlock請求到達的速率就是1Tarrive${\displaystyle \frac{1}{T_{arrive}}}$(事實上應該是泊松分佈)，由於我們的思想實驗基於多核CPU平臺，因此總體上的spinlock請求到達的速率和空閒CPU個數成正比。假設當前的n$n$核CPU系統上已經有k$k$個CPU在自旋等鎖了，那麼n−k$n-k$個CPU上spinlock的到達速率為n−kTarrive${\displaystyle \frac{n-k}{T_{arrive}}}$，因此，上圖中的A[k]$A[k]$便求了出來：

A[k]=n−kTarrive$A[k]={\displaystyle \frac{n-k}{T_{arrive}}}$

現在考慮釋放鎖的過程導致的狀態轉換。

先理解狀態S[k]$S[k]$的意義，S[]$S[]$這裡是的是Service，相應的對應A[]$A[]$則表示Arrival，所謂的服務時間指的是從當前CPU獲得spinlock到該spinlock成功轉給下一個CPU之間的時間！這部分時間包括兩個部分，一個部分是執行lock/unlock之間程式碼的時間E$E$，另一部分時間指的是unlock操作中消耗的時間，我們把這部分時間設為R$R$，現在的問題轉化為根據以上的資訊，求出R$R$的表示式。

我們在討論中有個假設，即我們思想實驗的平臺對cache一致性中update的管理方式是點對點one by one的unicast方式，而不是broadcast的方式，設處理一個CPU的update時間為c$c$，那麼在k$k$個CPU同時自旋等鎖的條件下，所有的CPU的cache line全部更新的時間就是k×c$k\times c$，由於ticket spinlock是嚴序的，而cache line update的到達先後卻不可控制，因此下一個獲得鎖的CPU的cache line得到更新的時間平均值為k×c2${\displaystyle \frac{k\times c}{2}}$，即平均在這個時間後，下一個CPU即可以成功獲取鎖，從spin_lock自旋狀態返回。於是，我們有：

S[k]=1E+k×c2$S[k]={\displaystyle \frac{1}{E+{\displaystyle \frac{k\times c}{2}}}}$

以上關於A[k]$A[k]$和S[k]$S[k]$的表示式非常好理解，我們可以看到，請求的到達速率，即spin_lock的速率是和空閒CPU數量，即不在自旋狀態的CPU數量成正比的，顯然地，空閒CPU越多，請求越容易到達，相反，spin_unlock的速率，即S[k]$S[k]$，則是和當前自旋狀態的CPU數量成反比的，至少是負相關的，因為自旋狀態的CPU越多，更新這麼多CPU的cache line的時間開銷就越大，這意味著服務速率S[k]就會越小。

有了上面基本的結論，加上下面一個穩態下Markov chain狀態轉換率守恆的基本原則，就可以匯出模型本身了：