我們知道，先序和中序或者後序與中序都可以唯一確定一棵樹，但是先序和後序不行。

今有兩個需求：判斷兩棵樹是否元素相等或是否元素對稱。

方法1：先序和中序或者中序和後序可以唯一確定一棵樹，那麼我們把他們遍歷生成的特徵序列對比即可判斷。

判相等：用遞迴函式，引數是兩棵樹的跟節點，兩個節點採取任意一種遍歷方式，以先序為例，return common(root1->left,root2->left)&&common(root1->right,root2->right)。

判定條件：如果一個指標空一個不空直接false，否則比對元素值，不相等則false，相等則繼續遞迴。

判對稱【左樹左孩子等於右樹右孩子】：return common(root1->left,root2->right)&&common(root1->right,root2->left)。

另一種處理方式：可以把他們的特徵序列用string存下來再比對，注意需要設定一個分隔符，而且如果是特徵序列則需要同時判先序+中序或後序+中序。

同時遞迴不用判兩種的原因在於，遞迴的過程本身會帶有一個時間戳，而當組合成特徵序列後，時間戳的資訊會丟失。

方法2：類似於特徵序列，但是更為強大。

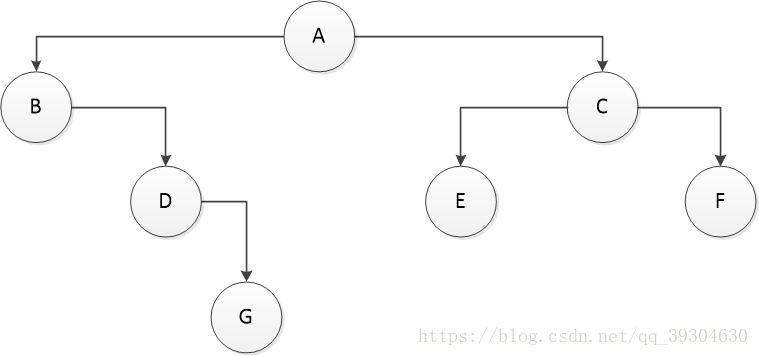
我們用_作為分隔符，用#表示空節點。

該樹的先序序列化為A_B_#_D_#_G_#_#_C_E_#_#_F_#_#_。

解釋一下為什麼需要分隔符_:       

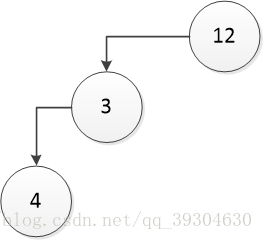
如你所見，如果不加分隔符，這兩棵樹明明是不同的兩棵樹，可是先序序列化的結果都是123#4##。

解釋一下為什麼需要#：               

如果所見，他們的先序序列化結果都是12_3_4。

結論：分隔符和空節點佔位符都是必要的。

解題：A.判相等，各自生成先序序列化結果再比對即可

           B.判對稱，同樣的，只要將第二棵樹遍歷的順序改為先右孩子再左孩子，生成序列後，比對即可。