如果想看NFA轉換成DFA，請關注我找到子集構造法NFA轉換成DFA這一篇

或者點選這個：https://blog.csdn.net/zcb1592781470/article/details/84643101

FA的最小化就是尋求最小狀態DFA

最小狀態DFA的含義: 
1.沒有多餘狀態(死狀態)

除多餘狀態 
什麼是多餘狀態？ 
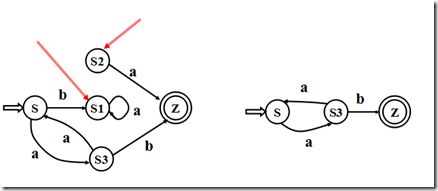
從這個狀態沒有通路到達終態；S1 
從開始狀態出發，任何輸入串也不能到達的那個狀態。S2 
如何消除多餘狀態？ 
刪除

2. 沒有兩個狀態是互相等價（不可區別） 
兩個狀態s和t等價的條件： 
相容性（一致性）條件——同是終態或同是非終態 
傳播性（蔓延性）條件——對於所有輸入符號，狀態s和狀態t必須轉換到等價的狀態裡。。

DFA的最小化—例子，第一步都是固定的。分成終態和非終態

１．將Ｍ的狀態分為兩個子集一個由終態k1=｛Ｃ，Ｄ，Ｅ，Ｆ｝組成，一個由非終態k2=｛Ｓ，Ａ，Ｂ｝組成，

２．考察｛Ｓ，Ａ，Ｂ｝是否可分．

因為Ａ經過a到達C屬於k1.而S經過a到達A屬於k2.B經過a到達A屬於k2，所以K2繼續劃分為{S，B},{A},

３．考察｛Ｓ，Ｂ｝是否可再分：

B經過b到達D屬於k1.S經過b到達B屬於k2，所以S，B可以劃分。劃分為{S},{B}

４．考察｛Ｃ，Ｄ，Ｅ，Ｆ｝是否可再分： 
因為Ｃ，Ｄ，Ｅ，Ｆ經過a和b到達的狀態都屬於｛Ｃ，Ｄ，Ｅ，Ｆ｝=k1所以相同，所以不可再分：

５．｛Ｃ，Ｄ，Ｅ，Ｆ｝以｛Ｄ｝來代替則，因為CDEF相同，你也可以用C來代替。無所謂的最小化的ＤＦＡ如圖，：