輸入：s = “abcdefghijklmnop”

輸出：

abcde
p   f
o   g
n   h
mlkji

思路：計算座標即可。關鍵在於中間部分，觀察知第一列和最後一列座標相加為15 + 5 = 20 = 5*（n-1）

import sys
s = "abcdefgh"  #樣例
k = len(s)  #總數
n = (k+4)//4  #邊長

print(s[0:n]) #第一行
for i in range(1, n-2+1):
    print(s[k-i] + " " * (n-2) + s[5*(n-1) - (k-i)])
print(s[3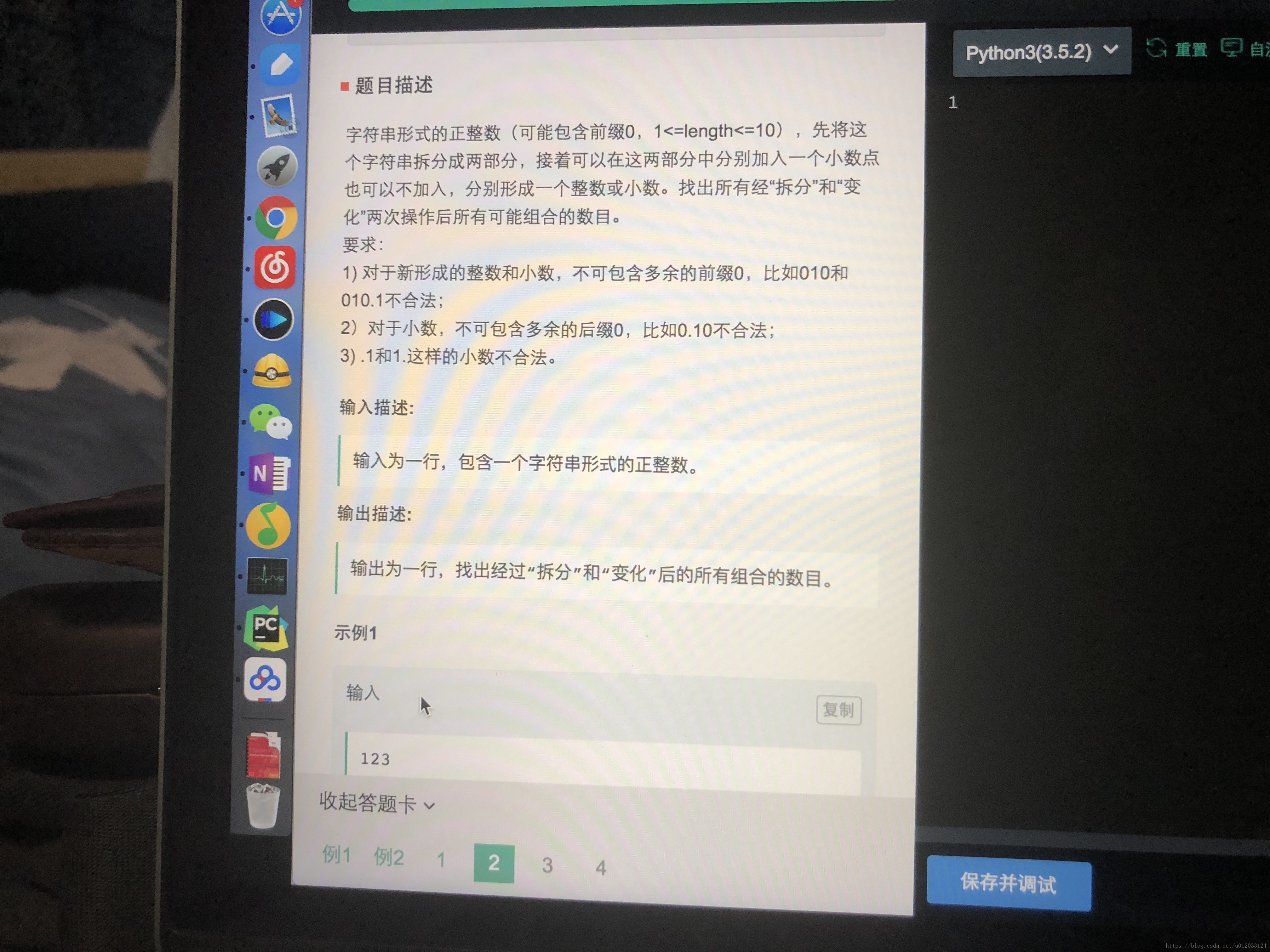
 
*n-3:2*n-3:-1])  #最後一行

輸入：123
輸出：4
輸入：00011
輸出：2

思路：求出所有劃分，對每一種劃分出的字串a，b：
1.若a、b直接為0，則只有一種組合方式
2.若末尾和開頭都為0，非法，0種
3.若末尾或開頭為0，只能有一種
4.末尾開頭都不為0，有len(a)種：不加’.’，或每兩位之間加’.’

（只過了5%，不知道問題在哪）
發現想複雜了，原本想題目求的是“組合”數，即（11，1.1），（1.1，11）是同一種情況。後來發現沒那麼複雜，可以當做是不同情況，這樣就不用考慮去重，即a==b的時候結果依然是兩者的笛卡爾積

import sys
num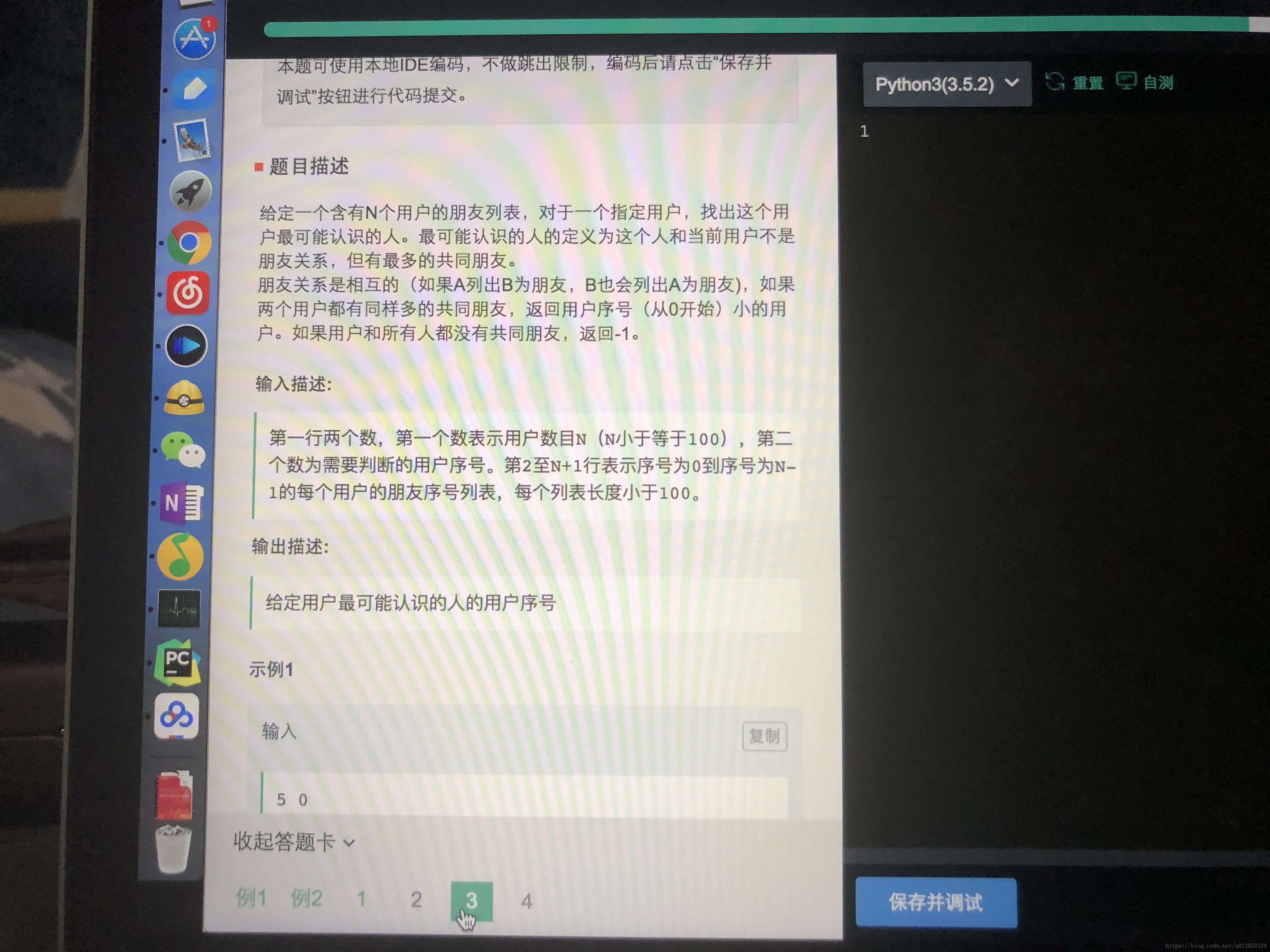
 
 = sys.stdin.readline()[:-1]  #除去換行符
sum = 0
for i in range(1, len(num)):  #列舉所有劃分
    a, b = num[0:i], num[i:]
    print(a,b)
    count_a, count_b = 0, 0
    if a == '0':
        count_a = 1
    elif a[0] == '0' and a[-1] == '0':
        count_a = 0
    elif a[-1] == '0' or a[0] == '0':
        count_a = 1
    else
 
:
        count_a = len(a)

    if b == '0':
        count_b = 1
    elif b[0] == '0' and b[-1] == '0':
        count_b = 0
    elif b[-1] == '0' or b[0] == '0':
        count_b = 1
    else:
        count_b = len(b)
    #笛卡爾積    
    sum += count_a * count_b  
print(sum)

輸入

5 0
1 2 3
0 4
0 4
0 4
1 2 3

輸出：

4

思路：用集合，每個使用者的朋友列表求交集，最大的為最可能認識的人

import sys
#n為使用者數，target為所求使用者序號
n, target = map(int, sys.stdin.readline().split())

users = []  #所有使用者分別做成集合
for i in range(n):
    friends = sys.stdin.readline().split()
    friends = [ int(f) for f in friends]
    friends = set(friends)
    users.append(friends)

tar_set = users[target]  #所求使用者的朋友集
best = -1  #最可能認識的序號
best_count = -1  #最大交集計數

for i in range(n):
    if i == target or (i in tar_set):  #不與自身以及自身的直接朋友做交集
        continue
    cfriends = tar_set & users[i]  #求交集
    count = len(cfriends)
    if count > best_count:  #找到更大交集
        best_count = count
        best = i
print(best)