題解 P4277 【河城荷取的煙花】
學校的一場考試:
技能比拼,分組方案,勇士的篝火
1.國王要嫁女兒啦!OI村莊裡的勇士們都想去試試,但是(不好的事都叫但是)......
2.經過OI村子裡的內部選拔,很多勇士都獲得了村長的青睞,村長為了......
3.OI村莊的勇士如願娶了國王女兒,村長打算......
講了由村長暗箱操作讓一群QIER勇士娶一位公主的故事
由情節就能看出資料水的一批
【河城荷取的煙花】的情節就美了很多
T3中出現了一個美觀扭曲的圖片:
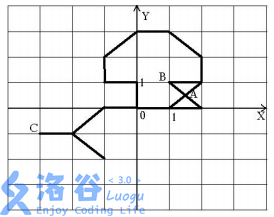
題意:
現需燃盡一攤奇怪的繩子(學校裡是木棍,差不多),要找一個整點點火,使得燃盡時間最短
要明白火的(此題中)特性
- 點燃後,火會沿著木棍向前方燃燒,可以點燃與它相接的木棍
- 只能在木棍的兩端點燃
下面是一些沒多大用處的話:
知識點:構圖+最短路應用
在此題中是一個連通圖,如果我們直接構圖處理比較複雜~~根本不會~~。
我們對原問題進行轉換:
由於繩&棍與繩&棍之間只能在繩&棍的兩端或中間相交。我們把每根繩&棍拆分成兩根相等的小繩&棍,這樣,繩&棍的數量增加了一倍。
原問題就轉化為,繩&棍與繩&棍之間只能在繩&棍的兩端相交,這樣處理起來就比較方便。
我們以繩&棍為邊,繩&棍與繩&棍之間的交點為頂點,構建一個連通圖,問題變為尋找一個合適的頂點,使得點燃以後完全燃燒的時間最短。
有用的:
- 一個繩&棍可拆成兩截小的繩&棍
- 很(“顯然”是沒有原因的),燃燒時間等於點燃的頂點到圖中最遠點的時間,如下圖:

由上述,需求最短路:
於是我們~~怎麼會有我~~可以利用Floyd's演算法求出任意兩點間的最短距離
餘下還需檢查每一條&根 繩&棍是否燃盡
當然,如果沒有完全燃燒,應求出剩餘邊燃燒所需最長時間
一些有(有?)用的話:
對於燃燒時間為L的木棍,它的兩端被點燃的時刻為T1和T2
如果T1 = T2+L 或者是 T2 = T1+L,那麼燃燒到T1 和 T2 的最大時刻,這根木棍己經完全燃燒
如果T1與T2之間的時間差不等於L,那麼就說明火是從不同的路徑燃燒到這根木棍的兩端。火將從兩端向中間燃燒,並在木棍內的某個點燃完
在簡單情況中,如果是從兩端同時點燃,燃燒時間為L/2。
更一般地,如果T1與T2不等,我們設一端是從0時刻點燃,另一端是從T時刻點燃,那麼這根木棍的燃燒時間為
T + (L-(T-0))/2
即,一端先燃燒T時間後,另一端才開始燃燒,完全燃燒後的時間為
(L-(T-0))/2
Floyd's :
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 double max(double a,double b) 6 { 7 if(a>b)return a; 8 else return b; 9 } 10 double min(double a,double b) 11 { 12 if(a<b)return a; 13 else return b; 14 } 15 int n; 16 int a1,a2,b1,b2,a1_5,b1_5,a[10001][10001]; 17 double t; 18 double e[3001][3001],dis[3001][3001]; 19 int tot=0; 20 bool mid[3001]; 21 double minx=0x7fffffff,maxx=-0x7fffffff; 22 int main() 23 { 24 memset(dis,0x7fffffff,sizeof(dis)); 25 memset(e,0x7fffffff,sizeof(e)); 26 memset(mid,false,sizeof(mid)); 27 scanf("%d",&n); 28 for(register int i=1;i<=n;i++) 29 { 30 scanf("%d%d%d%d%lf",&a1,&b1,&a2,&b2,&t); 31 a1=a1*2+400,b1=b1*2+400,a2=a2*2+400,b2=b2*2+400; 32 a1_5=(a1+a2)/2; 33 b1_5=(b1+b2)/2; 34 if(!a[a1][b1])a[a1][b1]=++tot; 35 if(!a[a2][b2])a[a2][b2]=++tot; 36 if(!a[a1_5][b1_5]) 37 { 38 a[a1_5][b1_5]=++tot; 39 mid[tot]=true; 40 } 41 e[a[a1][b1]][a[a1_5][b1_5]]=t*1.00000/2; 42 e[a[a1_5][b1_5]][a[a1][b1]]=t*1.00000/2; 43 e[a[a2][b2]][a[a1_5][b1_5]]=t*1.00000/2; 44 e[a[a1_5][b1_5]][a[a2][b2]]=t*1.00000/2; 45 dis[a[a1][b1]][a[a1_5][b1_5]]=t*1.00000/2; 46 dis[a[a1_5][b1_5]][a[a1][b1]]=t*1.00000/2; 47 dis[a[a2][b2]][a[a1_5][b1_5]]=t*1.00000/2; 48 dis[a[a1_5][b1_5]][a[a2][b2]]=t*1.00000/2; 49 } 50 for(register int k=1;k<=tot;k++) 51 { 52 for(register int i=1;i<=tot;i++) 53 { 54 for(register int j=1;j<=tot;j++) 55 { 56 if(dis[i][k]<0x7fffffff&&dis[k][j]<0x7fffffff) 57 { 58 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]); 59 } 60 } 61 } 62 } 63 for(register int k=1;k<=tot;k++) 64 { 65 if(mid[k])continue; 66 maxx=-0x7ffffff; 67 for(register int i=1;i<=tot;i++)maxx=max(maxx,dis[k][i]); 68 for(register int i=1;i<=tot;i++) 69 { 70 for(register int j=1;j<=tot;j++) 71 { 72 if(dis[k][i]<e[i][j]+dis[k][j]&&dis[k][j]<dis[k][i]+dis[i][j]) 73 { 74 maxx=max(maxx,max(dis[k][i],dis[k][j])+(e[i][j]-max(dis[k][i],dis[k][j])+min(dis[k][i],dis[k][j]))/2.0); 75 } 76 77 } 78 } 79 minx=min(minx,maxx); 80 } 81 printf("%.4lf",minx); 82 return 0; 83 }
其實,只要不直接抄題解,Ctrl+c & Ctrl+v 挺好的
但是(前面說過“但是”不是一個很好的詞)上面這段程式碼交上洛谷不可能對
上程式碼是針對我校OJ的題,資料水的一批,擷取:
【資料範圍】
100%的資料:
1<=n<=40;
|a|,|b|,|c|,|d|≤200, 0≤t≤1e7;
運用鄰接矩陣等知識點,10分不錯了
做最短路方法太多了,例如SPFA,中國演算法當然要用(模板好套)
有了前面程式碼的基礎當然好寫
奉上:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 double max(double a,double b) 6 { 7 if(a>b)return a; 8 else return b; 9 } 10 double min(double a,double b) 11 { 12 if(a<b)return a; 13 else return b; 14 } 15 struct node 16 { 17 int from,to; 18 double val; 19 int nxt; 20 node(int from=0,int to=0,double val=0,int nxt=0):from(from),to(to),val(val),nxt(nxt){}; 21 }; 22 int n,tot=0,len=0; 23 double val; 24 int a1,a2,b1,b2,am,bm; 25 int f[10000]; 26 node edge[20000]; 27 int head[10000],a[4000][4000]; 28 double dis[10000]; 29 bool vis[10000]; 30 double ans=0x7fffffff; 31 void add(int from,int to,double val) 32 { 33 edge[++len]=node(from,to,val,head[from]); 34 head[from]=len; 35 } 36 int Num(int x,int y) 37 { 38 if(!a[x][y])a[x][y]=++tot; 39 return a[x][y]; 40 } 41 void SPFA(int s) 42 { 43 deque<int> q; 44 memset(vis,0,sizeof(vis)); 45 memset(dis,127,sizeof(dis)); 46 dis[s]=0; 47 q.push_front(s); 48 vis[s]=1; 49 while(!q.empty()) 50 { 51 int cur=q.front(); 52 q.pop_front(); 53 vis[cur]=0; 54 for(register int i=head[cur];i;i=edge[i].nxt) 55 { 56 int id=edge[i].to; 57 if(dis[id]>dis[cur]+edge[i].val) 58 { 59 dis[id]=dis[cur]+edge[i].val; 60 if(!vis[id]) 61 { 62 vis[id]=true; 63 if(q.empty())q.push_front(id); 64 else 65 { 66 if(dis[id]<dis[q.front()])q.push_front(id); 67 else q.push_back(id); 68 } 69 } 70 } 71 } 72 } 73 } 74 double calculate(int x) 75 { 76 double s=max(dis[edge[x].from],dis[edge[x].to]); 77 s+=(edge[x].val-abs(dis[edge[x].from]-dis[edge[x].to]))/2; 78 return s; 79 } 80 double check(int x) 81 { 82 SPFA(x); 83 double ans=0; 84 for(register int i=1;i<=len;i+=2)ans=max(ans,calculate(i)); 85 return ans; 86 } 87 int main() 88 { 89 scanf("%d",&n); 90 for(register int i=1;i<=n;i++) 91 { 92 scanf("%d%d%d%d",&a1,&b1,&a2,&b2); 93 a1=a1*2+2000,a2=a2*2+2000,b1=b1*2+2000,b2=b2*2+2000; 94 am=(a1+a2)/2,bm=(b1+b2)/2; 95 scanf("%lf",&val); 96 val/=2; 97 add(Num(a1,b1),Num(am,bm),val); 98 add(Num(am,bm),Num(a1,b1),val); 99 add(Num(a2,b2),Num(am,bm),val); 100 add(Num(am,bm),Num(a2,b2),val); 101 f[Num(a1,b1)]=1; 102 f[Num(a2,b2)]=1; 103 } 104 for(register int i=1;i<=tot;i++)if(f[i])ans=min(check(i),ans); 105 printf("%.4lf",ans); 106 return 0; 107 }
這個SPFA自然是可過的

Floyd's演算法已經有大佬寫的很好,就不需要我的了~~
好不容易寫出來了,當然要發題解~~ ~~只有一篇,過的概率大一些~~
我要是過不去,豈不尷尬,求過o(╥﹏╥)o
謝謝Thanks♪(・ω・)ノ
再見ヾ( ̄▽ ̄)Bye~Bye~
