描述

在一個國家，長城的建造方式使每一堵長城都把兩個城鎮連在一起。長城不相交。因此，國家被劃分為這樣的地區：要從一個地區遷移到另一個地區，就必須穿過一個城鎮或跨過長城。對於任何兩個城鎮A和B，最多有一個長城，一端在A，另一個在B，而且，它可以走從A到B總是走在一個城鎮或沿著長城。輸入格式意味著附加限制。

有一個俱樂部的成員住在城鎮。每個城鎮只有一個成員，或者根本沒有成員。成員們想在其中一個地區(任何城鎮之外)開會。成員們騎著自行車旅行。他們不想進入任何城鎮，因為交通，他們想跨越儘可能少的長城，因為這是一個很大的麻煩。要進入會議區域，每個成員都需要跨越一個數(可能是0)的長城。他們希望找到這樣一個最優區域，使這些數字的和(簡稱交叉和)最小。

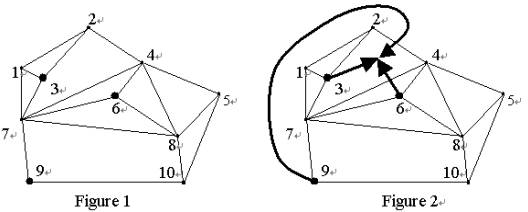
城鎮用從1到N的整數標記，其中N是城鎮的數目。在圖1中，標記的節點代表城鎮，連線節點的線代表長城。假設有三個成員，他們住在城鎮3，6和9。然後，圖2顯示了成員的最佳會議區域和各自的路徑。交叉金額為2：來自9鎮的成員必須在2和4鎮之間穿越長城，而來自6鎮的成員必須在4和7鎮之間橫渡。

您將編寫一個程式，給定城鎮、地區和俱樂部成員家鄉城鎮，計算最佳區域和最小交叉和。

輸入

您的程式是從標準輸入讀取。第一行包含一個整數：區域數M，2<=M<=200。第二行包含一個整數：城鎮數N，3<=N<=250。第三行包含一個整數：俱樂部成員數L，1<=L<=30，L<=N。第四行包含L個不同整數，按遞增順序排列：成員所在城鎮的標籤。

在此之後，輸入包含2M行，因此每個區域都有一對線：2m線的前兩行描述第一個區域，接下來的兩個描述第二個區域，以此類推。在這兩個人中，第一行顯示了該地區邊界上的城鎮數量。該對的第二行包含i整數：這些i城鎮的標籤按某種順序排列，在沿區域邊界順時針方向旅行時，它們可以傳遞，但有以下例外。最後一個區域是圍繞所有城鎮和其他地區的“外部區域”，因此標籤的順序對應於逆時針方向的行程。區域的順序給出了區域的整數標號：第一個區域有標號1，第二個區域有標號2，等等。請注意，輸入包括城鎮和長城形成的所有區域，包括“外部區域”。

輸出量

你的程式是寫到標準輸出。第一行包含一個整數：最小交叉和。

樣本輸入

10
10
3
3 6 9 
3
1 2 3 
3
1 3 7 
4
2 4 7 3 
3
4 6 7 
3
4 8 6 
3
6 8 7 
3
4 5 8 
4
7 8 10 9 
3
5 10 8 
7
7 9 10 5 4 2 1

樣本輸出

2

題解：將每一個區域看成點，若 i 區域與 j 區域相連則令mp[i][j]=1，再把圖建好後，進行進行floyd演算法求出區域間的最短路，最後列舉每一個區域得出最小值。

ac code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<set>
#include<map>
using namespace std;
#define N 305
#define inf 10000
int m,l,n;
struct e {
	int v;
	set<int>s;
};
e me[N];
set<pair<int, int> >q[N];
int mes[N], ts[N];
int mp[N][N], mx = inf;
int main() {
	int nu, p;
	memset(mp, inf, sizeof(mp));
	cin >> m >> n >> l;
	for (int i = 0; i < n; i++)
		me[i].v = 0;
	for (int i = 0; i < l; i++) {
		cin >> ts[i];
		me[ts[i]].v = 1;
	}
	int t = 0;
	for (int i = 0; i < m; i++) {
		scanf("%d", &nu);
		for (int j = 0; j < nu; j++) {
			scanf("%d", &mes[j]);
			if (me[mes[j]].v) {
				me[mes[j]].s.insert(i);
			}
			if (j > 0) {
				if (j == nu - 1) {
					q[i].insert(make_pair(mes[j], mes[0]));
					q[i].insert(make_pair(mes[0], mes[j]));
				}
				q[i].insert(make_pair(mes[j], mes[j - 1]));
				q[i].insert(make_pair(mes[j - 1], mes[j]));
			}
		}
	}
	//cout << "Y" << endl;
	for (int i = 0; i < n; i++)
		mp[i][i] = 0;
	for (int i = 0; i < m; i++) {
		for (int j = i + 1; j < m; j++) {
			for (set<pair<int,int> >::iterator ite = q[j].begin(); ite != q[j].end(); ite++) {
				if (q[i].count(*ite)) {
					//cout << ite->first << " " << ite->second << endl;
					mp[i][j] = 1;
					mp[j][i] = 1;
					break;
				}
			}
		}
	}
	for (int k = 0; k < m; k++) {
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < m; j++) {
				if (mp[i][j] > mp[i][k] + mp[k][j]) {
					mp[i][j] = mp[i][k] + mp[k][j];
				}
			}
		}
	}
	int sum = 0, sums =100000;
	for (int i = 0; i < m; i++) {
		sum = 0;
		for (int j = 0; j < l; j++) {
			mx = inf;
			for (set<int>::iterator ier = me[ts[j]].s.begin(); ier != me[ts[j]].s.end(); ier++) {
				//cout << i << " " << ts[j] << " " << *ier << " " << mp[i][*ier] << endl;
				mx = min(mx, mp[i][*ier]);
			}
			sum += (mx);
		}
		sums = min(sums, sum);
	}
	cout << sums << endl;
	return 0;
}