由於使用 Cocoa 框架能夠快速地建立一個可用的應用，這讓許多開發者都喜歡上了 OS X 或 iOS 開發。如今即使是小團隊也能設計和開發複雜的應用，這很大程度上要歸功於這些平臺所提供的工具和框架。Swift 的 Playground 不僅繼承了快速開發的傳統，並且有改變我們設計和編寫 OS X 和 iOS 應用方式的潛力。

向那些還不熟悉這個概念的讀者解釋一下，Swift 的 playground 就像是一個可互動的文件，在其中你可以輸入 Swift 程式碼讓它們立即編譯執行。操作結果隨著執行的時間線一步步被展示，開發者能在任何時候輸出和監視變數。Playground 既可以在現有的 Xcode 工程中進行建立，也能作為單獨的包存在。

Swift 的 playground 主要還是作為學習這門語言的工具而被重視，然而我們只要關注一下類似專案，如 IPython notebooks，就能看到互動程式設計環境在更廣闊的範圍內的潛在應用。從科學研究到機器視覺實驗，這些任務現在都使用了 IPython notebooks。這種方式也被用來探索其他語言的範例，如 Haskell 的函數語言程式設計。

接下來我們將探索 Swift 的 playground 在文件、測試和快速原型方面的用途。本文使用的所有 Swift playground 原始碼可以在這裡下載。

將 Playground 用於文件和測試

Swift 是一個全新的語言，許多人都使用 playground 來了解其語法和約定。不光是語言，Swift 還提供了一個新的標準庫。目前這個標準庫的文件中對於方法的說明不太詳細，所以雨後春筍般的湧現了許多像

編者注 在這裡有一份自動生成和整理的 Swift 標準庫文件，可以作為參考。

不過通過文件知道方法的作用是一回事，在程式碼中實際呼叫又是另一回事。特別是許多方法在新語言 Swift 的 collection class 中能表現出有趣的特性，因此如果能在 collections 裡實際檢驗它們的作用將非常有幫助。

Playground 展示語法和實時執行真實資料的特性，為編寫方法和庫介面提供了很好的機會。為了介紹 Collection 方法的使用，我們建立了一個叫 CollectionOperations.playground

例如，我們建立瞭如下的初始陣列：

let testArray = [0, 1, 2, 3, 4]

然後想試試 filter() 方法：

let odds = testArray.filter{$0 % 2 == 1}

最後一行顯示這個操作所得到的結果的陣列為： [1, 3]。通過實時編譯我們能瞭解語法、寫出例子以及獲得方法如何使用的說明，所有這些就如一個活的文件展示在眼前。

這對於其他的蘋果框架和第三方庫都奏效。 例如，你可能想給其他人展示如何使用 Scene Kit，這是蘋果提供的一個非常棒的框架，它能在 Mac 和 iOS 上快速構建3D場景。或許你會寫一個示例應用，不過這樣展示的時候就要構建和編譯。

在例子 SceneKitMac.playground 中，我們已經建立了一個功能完備帶動畫的 3D 場景。你需要開啟 Assistant Editor (在選單上依次點選 View | Assistant Editor | Show Assistant Editor)，3D 效果和動畫將會被自動渲染。這不需要編譯迴圈，而且任何的改動，比如改變顏色、幾何形狀、亮度等，都能實時反映出來。使用它能在一個互動例子中很好的記錄和介紹如何使用框架。

除了展示方法和方法的操作，你還會注意到通過檢查輸出的結果，我們可以驗證一個方法的執行是否正確，甚至在載入到 playground 的時候就能判斷方法是否被正確解析。不難想象我們也可以在 playground 裡新增斷言，以及建立真正的單元測試。或者更進一步，創建出符合條件的測試，從而在你打字時就實現測試驅動開發。

事實上，在 2014 年 7 月號的 PragPub 雜誌中，Ron Jeffries 在他的文章 “從測試驅動開發角度來看Swift” 中提到過這一觀點：

Playground 很大程度上會對我們如何執行測試驅動開發產生影響。Playground 能夠快速展示我們所能做的東西，因此我們將比之前走得更快。但是同過去的測試驅動開發框架結合在一起時，能否走的更好？我們是否能提煉出更好的程式碼，以滿足更少的缺陷數量和重構？

關於程式碼質量的問題還是留給別人回答吧，接下來我們一起來看看 playground 如何加快一個快速原型的開發。

建立 Accelerate 的原型 -- 經過優化的訊號處理

Accelerate 框架包括了許多功能強大的並行處理大型資料集的方法。這些方法可以利用例如 Intel 晶片中的 SSE 指令集，或者 ARM 晶片中的 NEON 技術等，這樣的現代 CPU 中向量處理指令的優勢。然而，相較於功能的強大，它們的介面似乎有點不透明，其使用的文件也有點缺乏。這就導致許多開發者無法使用 Accelerate 這個強大的工具所帶來的優勢。

Swift 提供了一個機會，通過方法過載或為 Accelerate 框架進行包裝後，可以讓互動更加容易。這已經在 Chris Liscio 的庫 SMUGMath 的實踐中被證實，這也正是我們接下來將要建立的原型的靈感來源。

假設你有一系列正弦波的資料樣本，然後想通過這些資料來確定這個正弦波的頻率和幅度，你會怎麼做呢？一個解決方案是通過傅立葉變換來算出這些值，傅立葉變換能從一個或多個重疊的正弦波提取頻率和幅度資訊。Accelerate 框架提供了另一個解決方案，叫做快速傅立葉變換 （FFT），關於這個方案這裡有一個 (基於 IPython notebook 的) 很好的解釋。

我們在例子 AccelerateFunctions.playground 中實現了這個原型，你可以對照這個例子來看下面的內容。請確認你已經開啟 Assistant Editor (在選單上依次點選 View | Assistant Editor | Show Assistant Editor) 以檢視每一階段所產生的圖形。

首先我們要產生一些用於實驗的示例波形。使用 Swift 的 map() 方法可以很容易地實現：

let sineArraySize = 64

let frequency1 = 4.0
let phase1 = 0.0
let amplitude1 = 2.0
let sineWave = (0..<sineArraySize).map {
    amplitude1 * sin(2.0 * M_PI / Double(sineArraySize) * Double($0) * frequency1 + phase1)
}

為了便於之後使用 FFT，我們的初始陣列大小必須是 2 的冪次方。把 sineArraySize 值改為像 32，128 或 256 將改變之後顯示的影象的密度，但它不會改變計算的基本結果。

要繪製我們的波形，我們將使用新的 XCPlayground 框架 (需要先匯入) 和以下輔助函式：

func plotArrayInPlayground<T>(arrayToPlot:Array<T>, title:String) {
    for currentValue in arrayToPlot {
        XCPCaptureValue(title, currentValue)
    }
}

當我們執行：

plotArrayInPlayground(sineWave, "Sine wave 1")

我們可以看到如下所示的圖表：

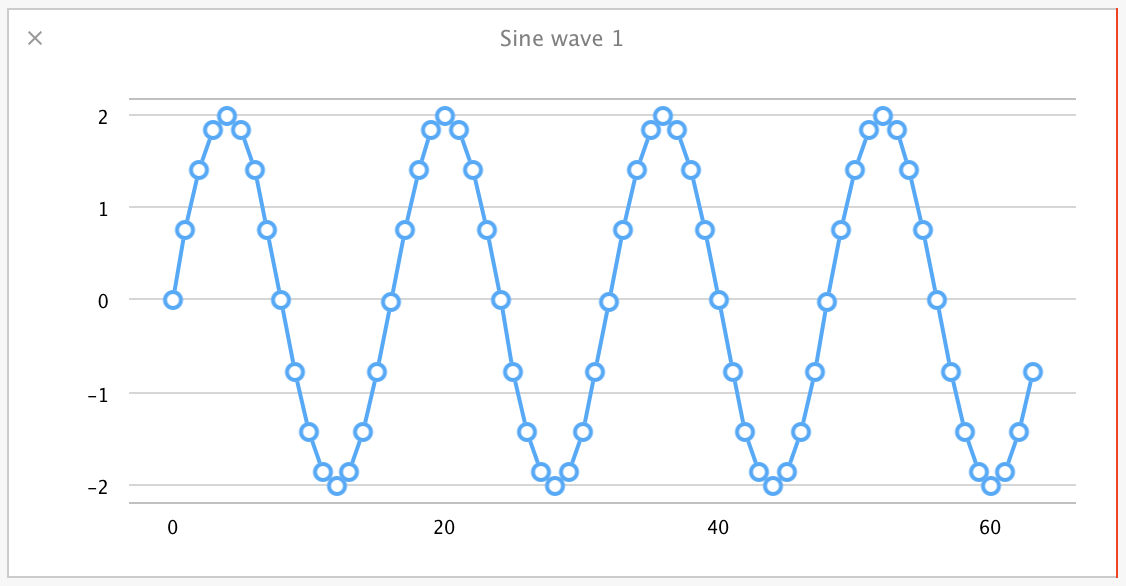
這是一個頻率為 4.0、振幅為 2.0、相位為 0 的正弦波。為了變得更有趣一些，我們建立了第二個正弦波，它的頻率為 1.0、振幅為 1.0、相位為 π/2，然後把它疊加到第一個正弦波上：

let frequency2 = 1.0
let phase2 = M_PI / 2.0
let amplitude2 = 1.0
let sineWave2 = (0..<sineArraySize).map {
    amplitude2 * sin(2.0 * M_PI / Double(sineArraySize) * Double($0) * frequency2 + phase2)
}

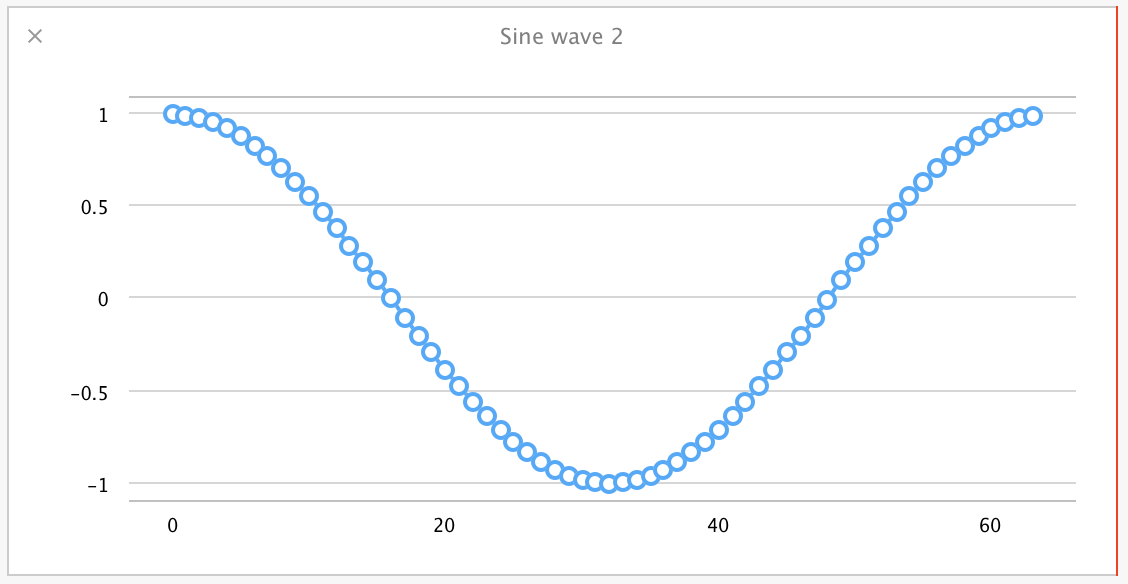
現在我們要將兩個波疊加。從這裡開始 Accelerate 將幫助我們完成工作。將兩個個獨立地浮點數陣列相加非常適進行合併行處理。這裡我們要使用到 Accelerate 的 vDSP 庫，它正好有這類功能的方法。為了讓這一切更有趣，我們將過載一個 Swift 操作符用於向量疊加。不巧的是 + 這個操作符已經用於陣列連線 (其實挺容易混淆的)，而 ++ 更適合作為遞增運算子，因此我們將定義 +++ 作為相加的運算子。

infix operator  +++ {}
func +++ (a: [Double], b: [Double]) -> [Double] {
    assert(a.count == b.count, "Expected arrays of the same length, instead got arrays of two different lengths")

    var result = [Double](count:a.count, repeatedValue:0.0)
    vDSP_vaddD(a, 1, b, 1, &result, 1, UInt(a.count))
    return result
}

上文定義了一個操作符，操作符能將兩個 Double 型別的 Swift 陣列中的元素依次合併為一個數組。在運算中建立了一個和輸入的陣列長度相等的空白陣列（假設輸入的兩個陣列長度相等）。由於 Swift 的一維陣列可以直接對映成 C 語言的陣列，因此我們只需要將作為引數的 Doubles 型別陣列直接傳遞給 vDSP_vaddD() 方法，並在我們的陣列結果前加字首 &。

為了驗證上述疊加是否被正確執行，我們可以使用 for 迴圈以及 Accelerate 方法來繪製合併後的正弦波的結果：

var combinedSineWave = [Double](count:sineArraySize, repeatedValue:0.0)
for currentIndex in 0..<sineArraySize {
    combinedSineWave[currentIndex] = sineWave[currentIndex] + sineWave2[currentIndex]
}

let combinedSineWave2 = sineWave +++ sineWave2

plotArrayInPlayground(combinedSineWave, "Combined wave (loop addition)")
plotArrayInPlayground(combinedSineWave2, "Combined wave (Accelerate)")

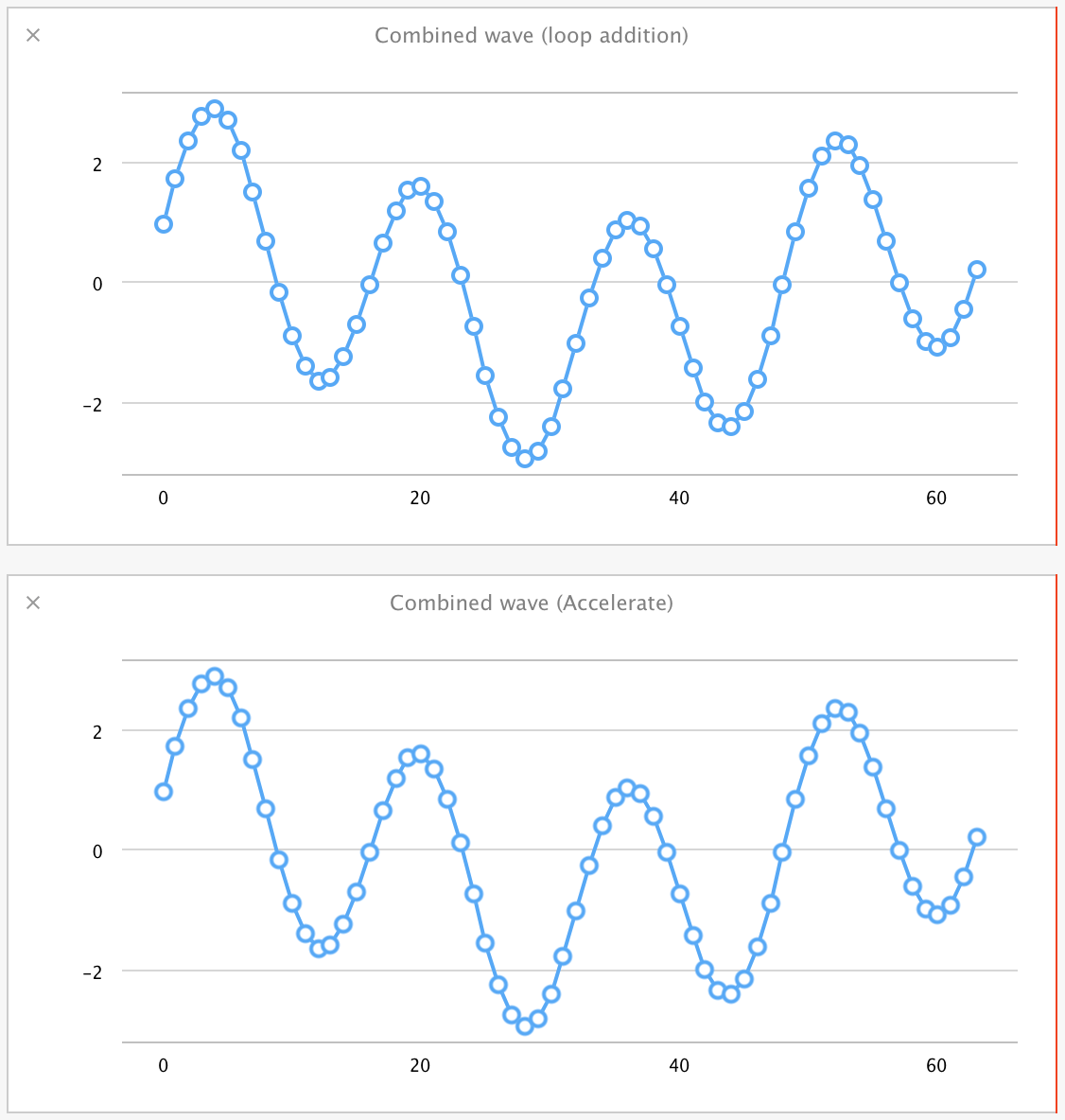
果然，結果是一致的。

在繼續 FFT 本身之前，我們需要另一個向量運算來處理計算的結果。Accelerate 的 FFT 實現中獲取的所有結果都是平方之後的，所以我們需要對它們做平方根操作。我們需要對陣列中的所有元素呼叫類似 sqrt() 方法，這聽上去又是一個使用 Accelerate 的機會。

Accelerate 的 vecLib 庫中有很多等價的數學方法，包括平方根的 vvsqrt()。這是個使用方法過載的好例子，讓我們來建立一個新版本的 sqrt()，使其能處理 Double 型別的陣列。

func sqrt(x: [Double]) -> [Double] {
    var results = [Double](count:x.count, repeatedValue:0.0)
    vvsqrt(&results, x, [Int32(x.count)])
    return results
}

和我們的疊加運算子一樣，過載的平方函式輸入一個 Double 陣列，為輸出建立了一個 Double 型別的陣列，並將輸入陣列中的所有引數直接傳遞給 Accelerate 中的 vvsqrt()。通過在 playground 中輸入以下程式碼，我們可以驗證剛剛過載的方法。

sqrt(4.0)
sqrt([4.0, 3.0, 16.0])

我們能看到，標準 sqrt() 函式返回2.0，而我們的新建的過載方法返回了 [2.0, 1.73205080756888, 4.0]。這的確是一個非常易用的過載方法，你甚至可以想象照以上方法使用 vecLib 為所有的數學方法寫一個並行的版本 (不過 Mattt Thompson 已經做了這件事)。在一臺 15 寸的 2012 年中的 i7 版本 MacBook Pro 中處理一個有一億個元素的陣列，使用基於 Accelerate 的 sqrt() 方法的執行速度比迭代使用普通的一維 sqrt() 快將近一倍。

有了這個以後，我們來實現 FFT。我們並不打算在 FFT 設定的細節上花費大量時間，以下是我們的 FFT 方法：

let fft_weights: FFTSetupD = vDSP_create_fftsetupD(vDSP_Length(log2(Float(sineArraySize))), FFTRadix(kFFTRadix2))

func fft(var inputArray:[Double]) -> [Double] {
    var fftMagnitudes = [Double](count:inputArray.count, repeatedValue:0.0)
    var zeroArray = [Double](count:inputArray.count, repeatedValue:0.0)
    var splitComplexInput = DSPDoubleSplitComplex(realp: &inputArray, imagp: &zeroArray)

    vDSP_fft_zipD(fft_weights, &splitComplexInput, 1, vDSP_Length(log2(CDouble(inputArray.count))), FFTDirection(FFT_FORWARD));
    vDSP_zvmagsD(&splitComplexInput, 1, &fftMagnitudes, 1, vDSP_Length(inputArray.count));

    let roots = sqrt(fftMagnitudes) // vDSP_zvmagsD returns squares of the FFT magnitudes, so take the root here
    var normalizedValues = [Double](count:inputArray.count, repeatedValue:0.0)

    vDSP_vsmulD(roots, vDSP_Stride(1), [2.0 / Double(inputArray.count)], &normalizedValues, vDSP_Stride(1), vDSP_Length(inputArray.count))
    return normalizedValues
}

第一步，我們設定了計算中需要使用到的 FFT 權重，它和我們要處理的陣列大小相關。這些權重將在稍後實際的 FFT 計算中被使用到，它可以通過 vDSP_create_fftsetupD() 計算得到，並且對於給定大小的陣列是可以重用的。因為在這裡陣列的大小是個恆定的常量，因此我們只需要計算一次權重，並將它作為全域性變數並在每次 FFT 中重用即可。

在 FFT 方法中，我們初始化了一個用於存放操作結果的陣列 fftMagnitudes，陣列的初始元素都為 0，大小為之前正弦波的大小。FFT 運算的輸入引數都是實部加上虛部的複數形式，但我們真正關心的只是它的實數部分，因此我們初始化 splitComplexInput 的時候使用輸入陣列作為實數部分，而將零作為虛數部分。然後 vDSP_fft_zipD() 和 vDSP_zvmagsD() 負責執行 FFT，並使用 fftMagnitudes 陣列來儲存 FFT 從 FFT 中得到的結果的平方數。

在這裡，我們使用了之前提到的基於 Accelerate 的 sqrt() 方法來計算平方根，返回實際大小，然後基於輸入陣列的大小對值進行歸一化。

對一個單一的正弦波，以上所有操作的的結果如下：

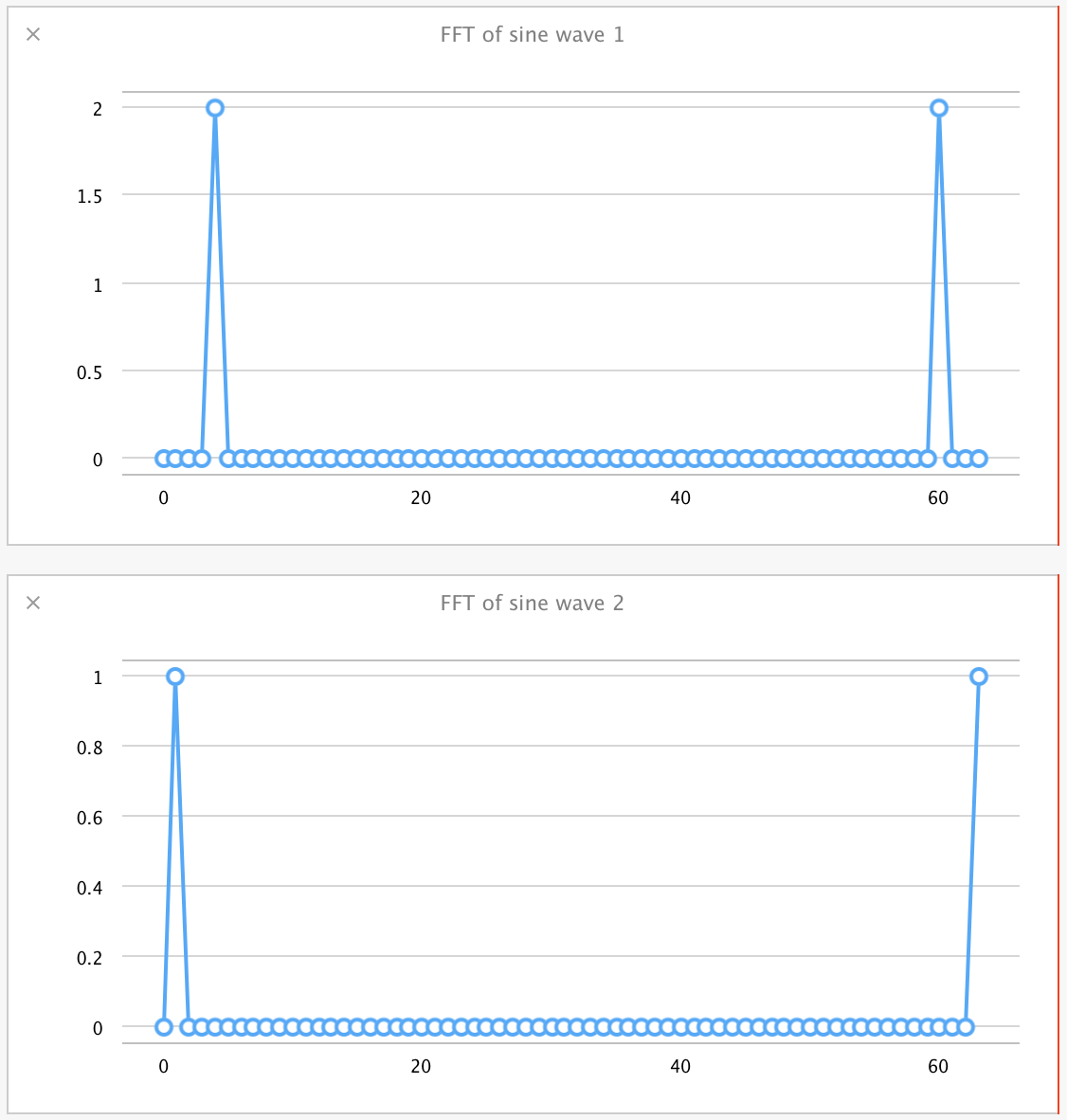
疊加的正弦波看起來像這樣：

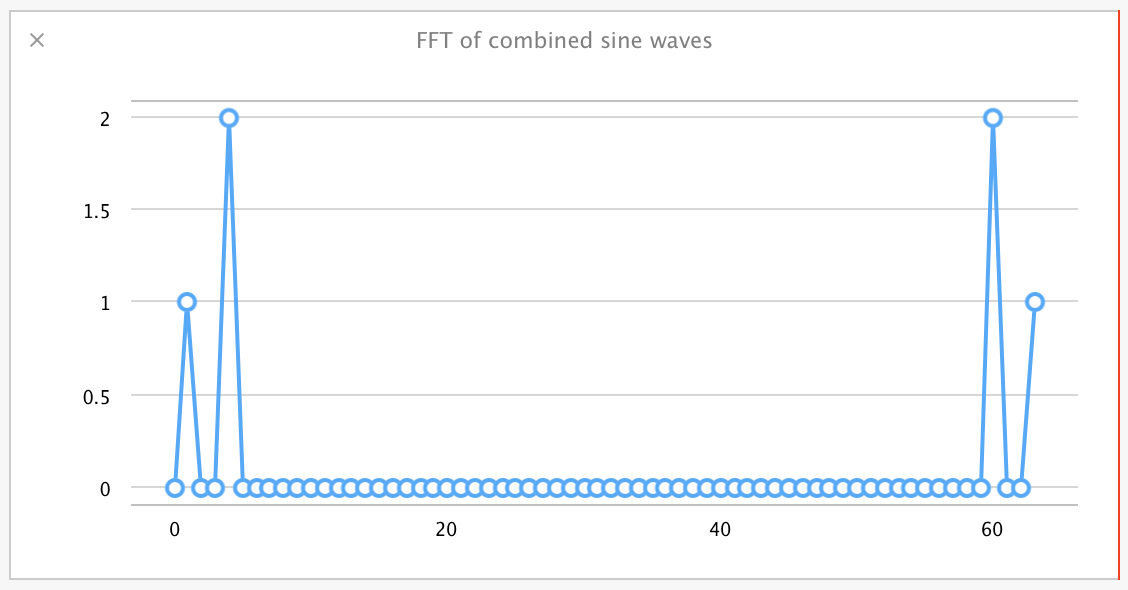
對這些值一個非常簡單的解釋是：這些結果表示了正弦波頻率的集合，從左邊開始，集合中的值表示了在該頻率下檢測到的波的振幅。它們關於中心對稱，因此你可以忽略圖中右半部分的值。

可以觀察到對於頻率為 4.0 振幅為 2.0 的波，在 FFT 中是一個 位於 4 對應於 2.0 的值。同樣對於頻率為 1.0 振幅為 1.0 的波，在 FFT 中是位於 1 對應值為 1.0 的點。儘管疊加後的正弦波得到的 FFT 波形比較複雜，但是依然能夠清晰地區分合並的兩個波在各自集合內的振幅和頻率，就彷彿它們的 FFT 結果是分別被加入的一樣。

再次強調，這是 FFT 運算的簡化版本，在上文的 FFT 程式碼中有簡化操作，但關鍵是在 playground 中通過一步步建立方法，我們能輕鬆地探索一個複雜的訊號處理操作，並且每一步操作的測試都能立即得到圖形反饋。

使用 Swift Playgrounds 快速建立原型的案例

我們希望這些例子能夠說明 Swift playground 在實踐新類庫和新概念上的作用。

上一個例子中的每一步裡，我們都能在執行時通過時間線中的圖案來觀察中間陣列的狀態。這對於一個示例程式來說作用非常大，而且也以某種方式為程式提供了介面。所有這些影象都實時更新，因此你能隨時返回到實現中並修改其中一個波的頻率或振幅，然後看著波形隨著處理步驟變化。這縮短了開發週期，並且對計算過程的體驗提供了巨大幫助。

這種立即反饋的互動式開發是為複雜的演算法建立原型的很好的案例。在將這樣的複雜演算法部署到實際的應用之前，我們有機會在 playground 中對它進行驗證和研究。