機器學習筆記(六):貝葉斯分類器
機器學習所研究的主要內容,是關於在計算機上從資料中產生“模型”的演算法,這個產生的模型大體上可以分為“判別式模型”和“生成式模型”兩大類。
其中判別式模型是給定x,通過直接對條件概率分佈P(y|x)進行建模來預測y。這種方法尋找不同類別的最優分類面,反映的是異類資料之間的差異。之前幾篇文章中介紹的SVM、決策樹、線性模型等都是屬於判別式模型。
生成式模型則是先對聯合概率分佈P(x,y)建模,然後再由此獲得P(y|x)。對後驗概率建模,從統計的角度表示資料的分佈情況,能夠反映同類資料本身的相似度。我們本篇文章介紹的貝葉斯分類器和後面將要介紹的隱馬爾科夫模型都是屬於生成式模型。
目錄
一、從分類任務說起
二、樸素貝葉斯分類器
三、半樸素貝葉斯分類器與貝葉斯網
一、從分類任務說起
給定資料集D={(x1,y1),(x2,y2),(x3,y3),……,(xn,yn)},其中xi為第i組資料的屬性集合,yi為第i組資料的標記。分類任務的目標旨在習得一個從xi到yi的對映f(xi)=yi,所以用於分類的機器學習演算法的任務就是依據x的特徵與標記y的關係來構造分類器f。
線上性模型中,我們假設x的特徵(a1,a2,…,an)與標記y之間存在著一種線性關係,即![]()
而在貝葉斯分類器中,我們假設標記y的取值與x的特徵(a1,a2,…an)服從某種特殊的分佈。
為了方便理解,這裡舉一個例子
假如y的可能類標記有m種,即y={c1,c2,…,cm}。
當x=x1時,我們不像判別式模型那樣直接預測出x1的標記,而是算出此時y取不同值的概率,即
P(c1|x1)、P(c2|x1)、……、P(cm|x1)
然後基於“最小化條件風險”的策略,從上述m個概率中選擇最優的一個,取其中的ci作為x1的預測標記。
最小化條件風險的定義如下:
假設有N種可能的類別樣本,即![]() ,
,![]() 是將一個真實標記為cj的樣本誤分類為ci所產生的損失。基於後驗概率P(ci|x)可獲得將樣本x分類為ci所產生的期望損失,即在樣本x上的“條件風險”
是將一個真實標記為cj的樣本誤分類為ci所產生的損失。基於後驗概率P(ci|x)可獲得將樣本x分類為ci所產生的期望損失,即在樣本x上的“條件風險”

為了便於介紹接下來的內容,這裡再複習一下貝葉斯公式
![]()
![]()
二、樸素貝葉斯分類器
不難發現,基於上面的貝葉斯公式來估計後驗概率P(c|x)的主要困難在於:類條件概率P(x|c)是所有屬性上的聯合概率,難以從有限的訓練樣本直接估計而得。為避開這個障礙,樸素貝葉斯分類器(naive Bayes classifier)採用了“屬性條件獨立性假設”:對已知類別,假設所有屬性相互獨立。換言之,假設每個屬性獨立地對分類結果發生影響。
基於屬性條件獨立性假設,上式可重寫為
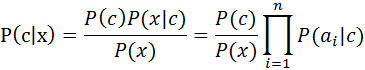
其中ai為x在第i個屬性上的取值
由於對所有類別來說P(x)相同,因此,上式又可以簡化為

這就是樸素貝葉斯分類器的表示式,顯然,樸素貝葉斯分類器的訓練過程就是基於訓練集D來估計先驗概率P(c),併為每個屬性估計條件概率P(ai|c)
此外,為了避免其他屬性攜帶的資訊被訓練集中未出現的屬性值“抹去”(例如:訓練集中屬性a1的取值只有1和2兩個值,但在測試時卻出現了新的值3,因為P(a1=3|c)=0,會直接導致![]() ),在估計概率值時通常要進行“平滑”,常用“拉普拉斯修正”。具體來說,令N表示訓練集D中可能的類別數,
),在估計概率值時通常要進行“平滑”,常用“拉普拉斯修正”。具體來說,令N表示訓練集D中可能的類別數,![]() 表示訓練集D中第c類樣本的集合,
表示訓練集D中第c類樣本的集合,![]() 表示Dc
表示Dc![]() 中在第i個屬性上取值為ai的樣本組成的集合,Ni
中在第i個屬性上取值為ai的樣本組成的集合,Ni![]() 表示第i個屬性可能的取值數。
表示第i個屬性可能的取值數。
則有:
![]()
![]()
顯然,拉普拉斯修正避免了因訓練集樣本不充分而導致概率估值為零的問題。
三、半樸素貝葉斯分類器與貝葉斯網路
為了降低貝葉斯公式中估計後驗概率P(c|x)的困難,樸素貝葉斯分類器採用了屬性條件獨立性假設,但在現實任務中這個假設往往很難成立。於是,人們嘗試對屬性條件獨立性假設進行一定程度的放鬆,由此產生了一類稱為“半樸素分類器(semi-naive Bayes classifiers)”的學習方法。
半樸素貝葉斯分類器的基本想法是適當考慮一部分屬性間的相互依賴資訊,從而既不需進行完全聯合概率計算,又不至於徹底忽略了比較強的屬性依賴關係。“獨依賴估計”是半樸素貝葉斯分類器最常用的一種策略。顧名思義,所謂“獨依賴”就是假設每個屬性在類別之外最多僅依賴於一個其他屬性,即
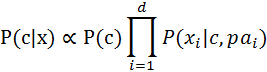
貝葉斯網(Bayesian network)亦稱“信念網”,它藉助有向無環圖(Directed Acyclic Graph,簡稱DAG)來刻畫屬性間的依賴關係,並使用條件概率表(Conditional Probability Table,簡稱CPT)來描述屬性的聯合概率分佈。半樸素貝葉斯分類器中常用“獨依賴估計”的策略,而貝葉斯網則表示能力更強,可以表示屬性間的多依賴關係。

一個貝葉斯網的例子
參考文獻
- 周志華,《機器學習》
- Lxjshuju,從貝葉斯方法談到貝葉斯網路,https://www.cnblogs.com/lxjshuju/p/6898457.html
