演算法導論之 B樹(B-樹)

阿新 • • 發佈：2018-12-23

作者：鄒祁峰
郵箱：[email protected]
日期：2014.03.13 18:00
轉載請註明來自"祁峰"的CSDN部落格

1 引言

In computer science, a B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children (Comer 1979, p. 123). Unlike self-balancing binary search trees, the B-tree is optimized for systems that read and write large blocks of data. It is commonly used in databases and filesystems.

在電腦科學中，B樹在查詢、訪問、插入、刪除操作上時間複雜度為O（log2~n）（2為底數 n為對數），與自平衡二叉查詢樹不同的是B樹對大塊資料讀寫的操作有更優的效能，其通常在資料庫和檔案系統中被使用。

一棵m階的B樹，或為空樹，或為滿足下列特徵的m叉樹：

①、樹中每個結點至多有m棵子樹；

②、若根結點不是終端結點，則至少有2棵子樹；

③、除根之外，所有非終端結點至少有棵子樹；

④、所有的非終端結點中包含下列資訊資料:

[n, C0, K0, C1, K1, C2, K2, ...., Kn-1, Cn]

其中：Ki[i=0,1，...，n-1]為關鍵字，且K

i<Ki+1[i=0, 1, ..., n-2]；Ci[i=0,1,...,n]為至上子樹根結點的指標，且指標Ci所指子樹中所有結點的關鍵字均小於Ki[i=0,1,...,n-1]，但都大於Ki-1[i=1,...,n-1]；

2 編碼實現

2.1 結構定義

根據m階B樹的性質，B樹的相關結構定義如下：

/* B樹結點結構 */
typedef struct _btree_node_t
{
    int num;                        /* 關鍵字個數 */
    int *key;                       /* 關鍵字：所佔空間為(max+1) - 多出來的1個空間用於交換空間使用 */
    struct _btree_node_t **child;   /* 子結點：所佔空間為（max+2）- 多出來的1個空間用於交換空間使用 */
    struct _btree_node_t *parent;   /* 父結點 */
}btree_node_t;

程式碼1 結點結構

/* B樹結構 */
typedef struct
{
    int max;                        /* 單個結點最大關鍵字個數 - 階m=max+1 */
    int min;                        /* 單個結點最小關鍵字個數 */
    int sidx;                       /* 分裂索引 = (max+1)/2 */
    btree_node_t *root;             /* B樹根結點地址 */
}btree_t;

程式碼2 B樹結構

2.2 建立B樹

此過程主要是完成btree_t中最大關鍵字個數max、最小關鍵字個數min、分裂索引sidx的設定，並建立一顆空樹，為後續的構造B樹做好準備條件。

/******************************************************************************
 **函式名稱: btree_creat
 **功    能: 建立B樹
 **輸入引數: 
 **     _btree: B樹
 **     m: 階 - 取值範圍m>=3
 **輸出引數: NONE
 **返    回: 0:成功 -1:失敗
 **實現描述: 
 **注意事項: 
 **     注意：引數max的值不能小於2.
 **作    者: # Qifeng.zou # 2014.03.12 #
 ******************************************************************************/
int btree_creat(btree_t **_btree, int m)
{
    btree_t *btree = NULL;

    if(m < 3) {
        fprintf(stderr, "[%s][%d] Parameter 'max' must geater than 2.\n", __FILE__, __LINE__);
        return -1;
    }

    btree = (btree_t *)calloc(1, sizeof(btree_t));
    if(NULL == btree) {
        fprintf(stderr, "[%s][%d] errmsg:[%d] %s!\n", __FILE__, __LINE__, errno, strerror(errno));
        return -1;
    }

    btree->max= m - 1;
    btree->min = m/2;
    if(0 != m%2) {
        btree->min++;
    }
    btree->min--;
    btree->sidx = m/2;
    btree->root = NULL; /* 空樹 */

    *_btree = btree;
    return 0;
}

程式碼3 建立B樹

2.3 插入操作

B樹是從空樹起，逐個插入關鍵字而建立起來的，由於B樹結點中的關鍵字個數num必須>=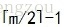

，因此，每次插入一個關鍵字不是在樹中新增一個終端結點，而是首先在最底層的某個非終端結點中插入一個關鍵字，若該結點的關鍵字個數不超過m-1，則插入完成，否則要進行結點的“分裂”。假設結點node的關鍵字個數num>max，則需進行分裂處理，其大體處理流程如下： 1) 結點node以sidx關鍵字為分割點，索引(0 ~ sidx-1)關鍵字繼續留在結點node中，索引(sidx+1 ~ num-1)關鍵字放入新結點node2中
2) 而索引sidx關鍵字則插入node->parent中，再將新結點node2作為父結點新插入關鍵字的右孩子結點
3) 判斷插入node的sidx關鍵字後，node->parent的關鍵字個數num是否超過max，如果超過，則以parent為操作物件進行1)的處理；否則，處理結束。
以下將通過構造一棵B樹的方式來講解B樹的插入過程：假設現在需要構建一棵4階B樹（即：階m=4、關鍵字最大個數max=3），其插入操作和處理過程如下描述。 1) 插入關鍵字45 剛開始為空樹，因此插入成功後只有一個結點。

圖1 插入結點 2) 插入關鍵字24和53 在圖1的基礎上，插入關鍵字24和53後，該結點關鍵字個數num仍未超過max，因此不會進行“分裂”處理。插入完成後，該結點關鍵字個數num=3已經達到臨界值max。

圖2 插入結點

3) 插入關鍵字90

在圖2基礎上，插入關鍵字90後，該結點關鍵字個數num=4超過max值，需要進行“分裂”處理。

圖3 分裂處理

當結點關鍵字個數num達到max時，則需要進行“分裂”處理，分割序號為num/2。圖3中的[4| 24, 45, 53, 90]的分割序號為num/2 = 4/2 = 2，序號從0開始計數，因此關鍵字53為分割點，分裂過程如下：

->1) 以序列號idx=num/2為分割點，原結點分裂為2個結點A[2| 24, 45]和B[1| 90]；

->2) 原結點無父結點，則新建一個結點P，並將關鍵字插入到新結點P中；

->3) 將結點A和B作為結點P的子結點，並遵循B樹特徵④；

->4) 因結點P的結點數未超過max，則分裂結束。

4) 插入關鍵字46和47

在圖3右圖的基礎上，插入關鍵字46和47後，得到圖4左圖，此時結點[4| 24, 45, 46, 47]已經達到分裂條件。

圖4 分裂處理

連續插入關鍵字46、47後，該結點[2| 24, 45]變為[4| 24, 45, 46, 47]，因此其達到了“分裂”的條件，其分裂流程如下：

->1) 以序列號idx=num/2為分割點，結點[2| 24, 45, 46, 47]分裂為兩個結點A[2| 24, 45]和B[1| 47]；

->2) 分割點關鍵字46被插入到父結點P中，得到結點P[2| 46, 53]

->3) 新結點B[1| 47]加入到結點P[2| 46, 53]的子結點序列中 - 遵循特徵④

->4) 因結點P[2| 46, 53]的關鍵字個數num為超過max，因為分裂結束。

5) 插入關鍵字15和18

在圖4右圖的基礎上，插入關鍵字15和18後，得到圖5左圖，此時結點[4| 15, 18, 24, 45]已經達到分裂條件。其處理過程同4），在此不再贅述。

圖5 分裂處理

6) 插入關鍵字48、49、50

在圖5右圖的基礎上插入48、49、50，可得到圖6左圖，此時結點[1| 47, 48, 49, 50]已達到分裂條件。

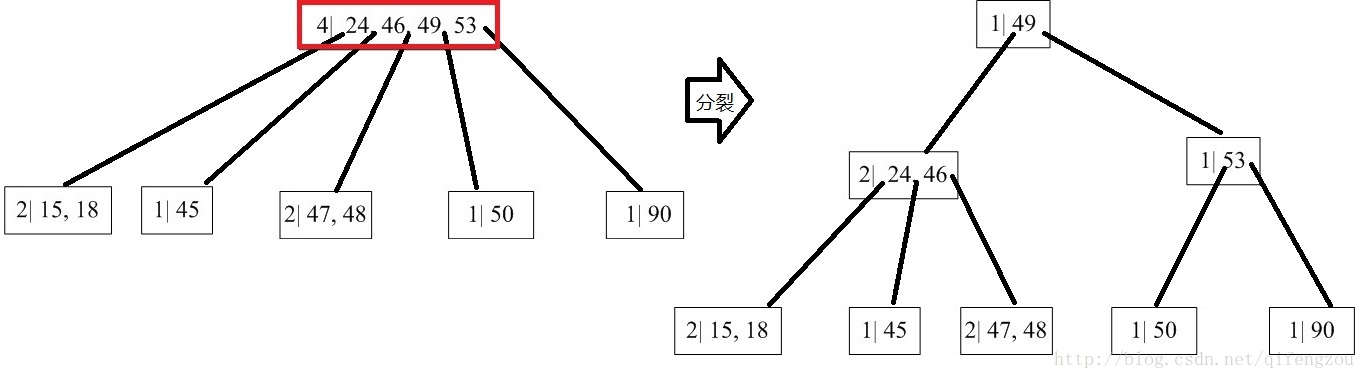
圖6 分裂處理

完成第一步分裂處理之後，父結點P[4| 24, 46, 49, 53]此時也達到了分裂條件。

圖7 進一步分裂

通過對1) ~ 6)的插入操作過程的理解和分析，可使用如下程式碼實現：

/******************************************************************************
 **函式名稱: btree_insert
 **功    能: 插入關鍵字（對外介面）
 **輸入引數: 
 **     btree: B樹
 **     key: 被插入的關鍵字
 **輸出引數: NONE
 **返    回: 0:成功 -1:失敗
 **實現描述: 
 **注意事項: 
 **作    者: # Qifeng.zou # 2014.03.12 #
 ******************************************************************************/
int btree_insert(btree_t *btree, int key)
{
    int idx = 0;
    btree_node_t *node = btree->root;

    /* 1. 構建第一個結點 */
    if(NULL == node) {
        node = btree_creat_node(btree);
        if(NULL == node) {
            fprintf(stderr, "[%s][%d] Create node failed!\n", __FILE__, __LINE__);
            return -1;
        }

        node->num = 1; 
        node->key[0] = key;
        node->parent = NULL;

        btree->root = node;
        return 0;
    }

    /* 2. 查詢插入位置：在此當然也可以採用二分查詢演算法，有興趣的可以自己去優化 */
    while(NULL != node) {
        for(idx=0; idx<node->num; idx++) {
            if(key == node->key[idx]) {
                fprintf(stderr, "[%s][%d] The node is exist!\n", __FILE__, __LINE__);
                return 0;
            }
            else if(key < node->key[idx]) {
                break;
            }
        }

        if(NULL != node->child[idx]) {
            node = node->child[idx];
        }
        else {
            break;
        }
    }

    /* 3. 執行插入操作 */
    return _btree_insert(btree, node, key, idx);
}

程式碼4 插入關鍵字（對外介面）

/******************************************************************************
 **函式名稱: _btree_insert
 **功    能: 插入關鍵字到指定結點
 **輸入引數: 
 **     btree: B樹
 **     node: 指定結點
 **     key: 被插入的關鍵字
 **     idx: 指定位置
 **輸出引數: NONE
 **返    回: 0:成功 -1:失敗
 **實現描述: 
 **注意事項: 
 **作    者: # Qifeng.zou # 2014.03.12 #
 ******************************************************************************/
static int _btree_insert(btree_t *btree, btree_node_t *node, int key, int idx)
{
    int i = 0;

    /* 1. 移動關鍵字:首先在最底層的某個非終端結點上插入一個關鍵字,因此該結點無孩子結點，故不涉及孩子指標的移動操作 */
    for(i=node->num; i>idx; i--) {
        node->key[i] = node->key[i-1];
    }

    node->key[idx] = key; /* 插入 */
    node->num++;

    /* 2. 分裂處理 */
    if(node->num > btree->max) {
        return btree_split(btree, node);
    }

    return 0;
}

程式碼5 插入結點

/******************************************************************************
 **函式名稱: btree_split
 **功    能: 結點分裂處理
 **輸入引數: 
 **     btree: B樹
 **     node: 需要被分裂處理的結點
 **輸出引數: NONE
 **返    回: 0:成功 -1:失敗
 **實現描述: 
 **注意事項: 
 **作    者: # Qifeng.zou # 2014.03.12 #
 ******************************************************************************/
static int btree_split(btree_t *btree, btree_node_t *node)
{
    int idx = 0, total = 0, sidx = btree->sidx;
    btree_node_t *parent = NULL, *node2 = NULL; 


    while(node->num > btree->max) {
        /* Split node */ 
        total = node->num;

        node2 = btree_creat_node(btree);
        if(NULL == node2) {       
            fprintf(stderr, "[%s][%d] Create node failed!\n", __FILE__, __LINE__);
            return -1;
        }

        /* Copy data */ 
        memcpy(node2->key, node->key + sidx + 1, (total-sidx-1) * sizeof(int));
        memcpy(node2->child, node->child+sidx+1, (total-sidx) * sizeof(btree_node_t *));

        node2->num = (total - sidx - 1);
        node2->parent  = node->parent;

        node->num = sidx; 
        /* Insert into parent */
        parent  = node->parent;
        if(NULL == parent)  {       
            /* Split root node */ 
            parent = btree_creat_node(btree);
            if(NULL == parent) {       
                fprintf(stderr, "[%s][%d] Create root failed!", __FILE__, __LINE__);
                return -1;
            }       

            btree->root = parent; 
            parent->child[0] = node; 
            node->parent = parent; 
            node2->parent = parent; 

            parent->key[0] = node->key[sidx];
            parent->child[1] = node2;
            parent->num++;
        }       
        else {       
            /* Insert into parent node */ 
            for(idx=parent->num; idx>0; idx--) {       
                if(node->key[sidx] < parent->key[idx-1]) {       
                    parent->key[idx] = parent->key[idx-1];
                    parent->child[idx+1] = parent->child[idx];
                    continue;
                }
                break;
            }       

            parent->key[idx] = node->key[sidx];
            parent->child[idx+1] = node2;
            node2->parent = parent; 
            parent->num++;
        }       

        memset(node->key+sidx, 0, (total - sidx) * sizeof(int));
        memset(node->child+sidx+1, 0, (total - sidx) * sizeof(btree_node_t *));

        /* Change node2's child->parent */
        for(idx=0; idx<=node2->num; idx++) {
            if(NULL != node2->child[idx]) {       
                node2->child[idx]->parent = node2;
            }       
        }       
        node = parent; 
    }

    return 0;
}

程式碼6 分裂處理

/******************************************************************************
 **函式名稱: btree_creat_node
 **功    能: 新建結點
 **輸入引數: 
 **     btree: B樹
 **輸出引數: NONE
 **返    回: 節點地址
 **實現描述: 
 **注意事項: 
 **作    者: # Qifeng.zou # 2014.03.12 #
 ******************************************************************************/
static btree_node_t *btree_creat_node(btree_t *btree)
{
    btree_node_t *node = NULL;


    node = (btree_node_t *)calloc(1, sizeof(btree_node_t));
    if(NULL == node) {
        fprintf(stderr, "[%s][%d] errmsg:[%d] %s\n", __FILE__, __LINE__, errno, strerror(errno));
        return NULL;
    }

    node->num = 0;

    /* More than (max) is for move */
    node->key = (int *)calloc(btree->max+1, sizeof(int));
    if(NULL == node->key) {
        free(node), node=NULL;
        fprintf(stderr, "[%s][%d] errmsg:[%d] %s\n", __FILE__, __LINE__, errno, strerror(errno));
        return NULL;
    }

    /* More than (max+1) is for move */
    node->child = (btree_node_t **)calloc(btree->max+2, sizeof(btree_node_t *));
    if(NULL == node->child) {
        free(node->key);
        free(node), node=NULL;
        fprintf(stderr, "[%s][%d] errmsg:[%d] %s\n", __FILE__, __LINE__, errno, strerror(errno));
        return NULL;
    }

    return node;
}

程式碼7 新建結點

2.4 結果展示

只需寫一個簡單的測試函式，呼叫以上的測試介面。隨機插入n個關鍵字，並列印其樹形結構，便可很方便的判斷出插入操作的正確性。
1) 設定B樹階m=3時

圖8 結果展示
2) 設定B樹階m=10時

圖9 結果展示

演算法導論之 B樹(B-樹)

1 引言

2 編碼實現

2.1 結構定義

2.2 建立B樹

2.3 插入操作

2.4 結果展示

演算法導論之平衡二叉樹 - 建立插入查詢銷燬 - 遞迴 C語言

演算法導論之平衡二叉樹 - 刪除 - 遞迴 C語言

演算法導論之平衡二叉樹

演算法導論之 B樹 B-樹 - 建立插入 C語言

演算法導論之 B樹 - 刪除 C語言

演算法導論之 B樹 B-樹

演算法導論之 B樹(B-樹)

演算法導論之 B-樹(B樹)

演算法導論第18章 B樹

演算法導論之紅黑樹 - 插入 C語言

演算法導論之紅黑樹

演算法導論之紅黑樹 - 刪除 C語言

演算法導論chapter12 二叉搜尋樹課後習題答案詳解

【資料結構與演算法】之二叉查詢樹 --- 第十三篇

演算法學習之重構二叉樹

演算法學習之實現二叉樹結點及其層數的非遞迴輸出

【演算法導論】求二叉樹的葉子數和深度

演算法練習之二叉查詢樹 C++實現

演算法導論習題練習——紅黑樹的插入和刪除

演算法導論思考題13-4 treap-樹堆

演算法導論 之 B樹(B-樹)

1 引言

2 編碼實現

2.1 結構定義

2.2 建立B樹

2.3 插入操作

2.4 結果展示

相關推薦

演算法導論之 B樹(B-樹)