前言

歡迎來到NOIP考前複習系列。。。。。。今天要講的是Dijkstra。。。

當然，如果有任何錯誤的話，歡迎留言指出喲。。。

演算法作用

Dijkstra演算法用於解決單源最短路問題，即求取從一個給定的起點出發到其他節點的最短距離。

演算法原理

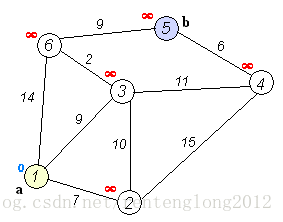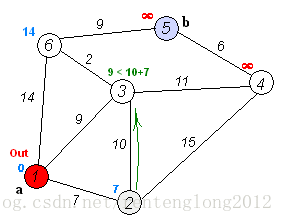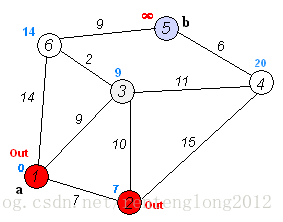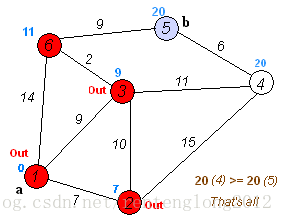
如圖：

我們首先定義一個數組dd，代表我們選定的起點到其他各個點的距離最小值。

然後，將dd陣列中除了起點以外的所有的元素都賦成INF（無限大）。

然後開始掃描起點所連線的點，找出一個直接距離最短的點，加入已生成的樹中，並將連線它們的這條邊加入最小生成樹中。

然後繼續，從已有的最小生成樹中的所有點出發，找到一個距離最近的，繼續加入生成樹。

演算法結果
演算法執行結束後，將會得到一個處理好的陣列dd，其中d[i]d[i]代表從起點出發到節點ii的最短路長度。

演算法實現
樸素方法
這個普通的寫法我並不想過多介紹，因為這樣做太過於普通，效率非常低。

你可以使用鄰接矩陣來儲存整個圖，然後每次列舉對應的行或列來找到一個距離最近的。

程式碼也比較簡單，這裡並不想過多描述。事實上，我一開始就寫的堆優化，因此再把它改成樸素演算法將會比較多餘。

堆優化
堆優化的主要思想就是使用一個優先佇列（就是每次彈出的元素一定是整個佇列中最小的元素）來代替最近距離的查詢，用鄰接表代替鄰接矩陣，這樣可以大幅度節約時間開銷。

在這裡有幾個細節需要處理：

首先來講，優先佇列的資料型別應該是怎樣的呢？
我們知道優先佇列應該用於快速尋找距離最近的點。由於優先佇列只是將最小的那個元素排在前面，因此我們應該定義一種資料型別，使得它包含該節點的編號以及該節點當前與起點的距離。

我們應該在什麼時候對佇列進行操作呢？
佇列操作的地方，首先就是搜尋剛開始，要為起點賦初始值，此時必須將起點加入優先佇列中。該佇列元素的節點編號為起點的編號，該節點當前與起點的距離為00。

那麼如果一個節點到起點的最短距離通過其他的運算流程發生了變化，那麼如何處理佇列中的那個已經存入的元素？
事實上，你不需要理會佇列中的元素，而是再存入一個就行了。因為如果要發生變化，只能將節點與起點之間的距離變得更小，而優先佇列恰好是先讓最小的那個彈出。

因此，輪到某一個佇列元素彈出的時候，如果有多個元素的節點編號相同，那麼被彈出的一定是節點編號最小的一個。等到後面再遇到這個節點編號的時候，我們只需要將它忽略掉就行了。