成為“黑客”前，必學的“密碼學原理”

”密碼學“是一個高度跨學科的領域，包含純數學、電腦科學以及電子工程等多方面的知識。 “許多小白看到這裡應該頭就大了”要學這麼多知識才能理解密碼學嗎?”當然不需要”如果你的理想是成為密碼學科學的研究者或者領域專家，一定要掌握上述學科知識。但是對於一名”初學者黑客”，我們僅需要了解密碼學的常規術語、密碼加密、密碼分析等密碼學基本體系就足夠了。

成為“黑客”前，必學的“密碼學原理”

一、 什麼是密碼學

官方定義：密碼學是研究編制密碼和破譯密碼的技術科學。研究密碼變化的客觀規律，應用於編制密碼以保守通訊祕密的，稱為編碼學;應用於破譯密碼以獲取通訊情報的，稱為破譯學，總稱密碼學。

通俗理解：密碼學是隱藏資訊的科學和藝術，因此它們是保密的，然後”取消隱藏”它們，以便只有預期的接收者才能閱讀它們。基本上，我們可以說密碼學是祕密訊息傳遞的科學。

二、 密碼學裡的常用術語解釋
　　

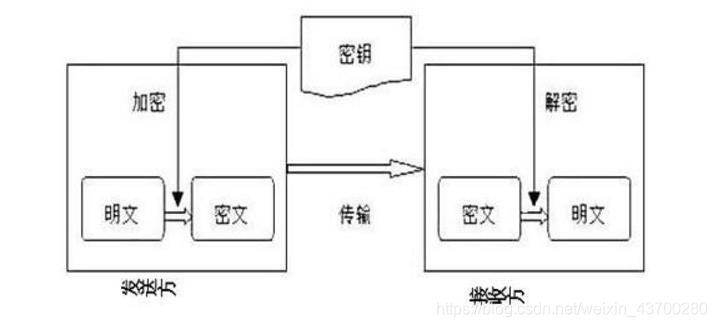
密碼學裡的常用術語

訊息也成為明文。

加密的訊息稱為密文。

E(M) = C,E為加密函式，M為明文，C為密文。

D© =M,D為解密函式，C為密文，M為明文 。

演算法和金鑰：如果演算法的保密性是基於保持演算法的祕密，這叫受限制的演算法。任何演算法都是可能被人逆向分析的，顯然這樣是不安全的。現代密碼學採用金鑰解決這個問題。金鑰用K表示，k1稱為加密金鑰，k2稱為解密金鑰，如果K1=K2,或者k2能從k1推算出來，反過來也成立，則這樣的演算法叫對稱演算法。如果k1不等於k2，並且k1與k2不能互相推匯出來，則這樣的演算法叫做非對稱方法，也叫公鑰演算法。

密碼分析：不知道金鑰的情況下，回覆出明文的科學。

隱寫術：將祕密訊息隱藏在其它訊息中。最常見的就是在影象中隱藏訊息，window下用copy命令直接可成功。

三、 密碼學的七個重要工具

密碼學的七個重要工具分別是：對稱密碼、公鑰密碼、單向雜湊函式、訊息認證碼、數字簽名、證書和偽隨機數生成器。

1. 對稱密碼

對稱密碼(symmetric cryptography)是指在加密和解密時使用同一金鑰的方式。它是最常見的一種加密方式，通過將資訊編碼，利用公開的加密演算法和保密的金鑰完成對資訊的加密和解密，其中加密過程和解密過程是對稱的，因此被稱為對稱密碼。

這裡出現了公開的加密演算法的概念，人們通常存在一種錯誤的觀點，即保密的加密演算法具有更高的安全性，這被現代密碼學稱之為”隱蔽式安全性”。因為保密的加密演算法只要被使用，遲早會公諸於世，想依靠對密碼演算法本身進行保密來確保機密性的密碼系統也就土崩瓦解了。相反，如果加密演算法從一開始就沒設想過要保密，則它會得到各種攻擊的洗禮，從而實現更強的保密性。因此現代密碼學的加密方式基本以”公開加密演算法+保密金鑰”組成。

組成：公開的加密演算法+保密的金鑰;

加密過程：A向B傳送加密資訊t時，需要利用加密演算法和金鑰對t進行加密;

解密過程：加密過程的逆過程;

優點：巨大的金鑰空間能夠抵禦暴力破解、演算法上沒有弱點可以抵禦其他型別的攻擊、加解密運算效率高等優點;

缺點：金鑰配送問題(這也是必須用到其它密碼技術的原因);

常見密碼演算法：DES、AES等;

用途：加密資訊;

2. 公鑰密碼

公鑰密碼(public-key cryptography)是指在加密和解密時使用不同金鑰的方式，與對稱金鑰正好相反，因此也被稱為非對稱密碼(asymmetric cryptography)。

組成：公開的加密演算法+公開金鑰(公鑰)+保密金鑰(私鑰);

加密過程：A向B傳送加密資訊t時，需要利用加密演算法和B的公鑰對t進行加密;

解密過程：B需要利用解密演算法(通常與加密演算法相同)和B的私鑰對t進行解密;

優點：解決了金鑰配送的問題;

缺點：加解密演算法效率低(意味著它無法直接用於資訊加密)，中間人攻擊(B無法確定密文是由A發來的，因此需要引入新的安全技術);

常見密碼演算法： RSA等;

用途：加密對稱金鑰等;

3. 單向雜湊函式

首先說明，後面這幾項技術都不是直接用於加密的。單向雜湊函式(one-way hash function)有一個輸入和一個輸出，其中輸入稱為訊息，輸出稱為雜湊值。它通過一個不可逆的函式y=f(x)將x對映為y，通過對比傳輸前後y的變化來判斷x是否被篡改。舉個例子：假設A要傳輸t給B，並且要能夠讓B判斷傳輸過程中是否有人修改過t，那怎麼做呢?A可以利用單向雜湊函式，求出y=f(t)，並將t和y一起發給B;B得到t和y後，利用f(t)=y1，判斷y和y1是否相同，不同則說明傳輸過程中t或y出現了錯誤，資訊不完整，相同則說明傳輸過程中t沒有被修改過。

組成：單向雜湊函式;

優點：演算法效率高、辨別篡改;

缺點：無法辨別偽裝(這就需要新的安全技術來保證);

常見密碼演算法：MD5、SHA1等;

用途：判斷篡改、基於口令的加密、訊息認證碼、數字簽名等;

4. 訊息認證碼

說到這裡，B仍然無法確定與他通訊的人是A。那如何認證A就是A呢?本節介紹的訊息認證碼(message authentication code)是一種確認完整性並進行認證的技術，簡稱MAC。它的思想很樸素，為了確保完整性，需要MAC與資訊內容相關，為了能夠認證，可以利用公共金鑰來提供。很顯然，MAC可以用單向雜湊函式與金鑰的組合來實現，這也是現實中MAC的一種實現方案。

組成：完整性技術(單向雜湊函式等)+保密金鑰;

加密過程：將金鑰作為完整性技術的種子引入，從而得到MAC;

認證過程：將資訊t做相同的操作，並與傳來的MAC對比，辨別偽裝;

優點：辨別篡改和偽裝;

缺點：存在金鑰傳遞的問題，當然可以引入公鑰方案解決，但又會引入中間人攻擊的問題(這也是數字簽名的作用)。另外也存在無法防止否認的問題;

常見密碼演算法：HMAC等;

用途：判斷篡改、認證;

5. 數字簽名

上一節提到了一種認證方案，但在某些場景下還存在諸多不足，如無法防止否認、無法抵禦中間人攻擊的問題。無法防止否認是因為金鑰相同，無法判斷誰發出了這條訊息，因此將金鑰分開為加密金鑰和解密金鑰就可以解決無法防止否認的問題。這是不是跟公鑰密碼很相似，可以將數字簽名看成是公鑰密碼的反過程，用私鑰加密來生成簽名，用公鑰解密來驗證簽名(這也要求不對稱加密演算法可逆，由此可是RSA多牛逼)。但前文討論過RSA演算法效率不高，因此數字簽名的做法通常：單向雜湊函式+RSA演算法。

組成：單向雜湊函式+公鑰密碼演算法+公鑰;

加密過程：A將資訊t經過單向雜湊函式運算得到h，利用A的私鑰對h加密得到數字簽名s;

認證過程：B收到t和s，利用A的公鑰對s進行解密，再將t雜湊，對比兩者是否一致即可。

優點：能夠識別篡改和偽裝，還可以防止否認;

缺點：由於用到了公鑰密碼，那仍然無法理想的解決中間人攻擊，因此提出了證書的概念;

常見密碼演算法：RSA等演算法組合;

用途：各種需要認證的場景;

6. 證書

通過上面的講解可以看出，密碼學的基礎是對稱密碼+公鑰密碼，但它們仍然無法抵禦中間人攻擊，也即M想辦法阻斷A和B的直接通訊，同時偽裝成B然後與A通訊，偽裝成A然後與B通訊。這個問題在密碼學看來就是個死迴圈，因此需要引入額外的技術——社會學知識：讓公鑰以及數字簽名技術成為一種社會性的基礎設施，即公鑰基礎設施(public key intrastructure)，簡稱PKI。而證書，就是將公鑰當作一條訊息，由一個可信的第三方對其簽名後所得到的公鑰。

7. 偽隨機數生成器

前面介紹的幾項技術彷彿能保證資訊的安全性，但其中仍然存在著坑：金鑰的由來以及各種演算法引數的由來。很顯然，如果它是由特定的序列來生成的，那麼攻擊者很容易就能推測出金鑰。那如何才能讓攻擊者沒法推測出來呢?那就是用隨機數。可又出現了一個問題，怎麼得到隨機數呢?一次次的扔硬幣肯定不行，那還是需要一個演算法來快速的生成類似隨機數的數，這就是偽隨機數生成器。因此這個偽隨機數生成器的演算法還是需要一番功夫的，這裡就不再贅述。

四、 現代密碼學常見的密碼演算法

1. 對稱演算法

對稱密碼演算法有時又叫傳統密碼演算法，就是加密金鑰能夠從解密金鑰中推算出來，反過來也成立。在大多數對稱演算法中，加密解密金鑰是相同的。這些演算法也叫祕密金鑰演算法或單金鑰演算法，它要求傳送者和接收者在安全通訊之前，商定一個金鑰。對稱演算法的安全性依賴於金鑰，洩漏金鑰就意味著任何人都能對訊息進行加密解密。只要通訊需要保密，金鑰就必須保密。

(1) DES：DES演算法的入口引數有三個：Key、Data、Mode。其中Key為7個位元組共56位，是DES演算法的工作金鑰;Data為8個位元組64位，是要被加密或被解密的資料;Mode為DES的工作方式,有兩種:加密或解密。其功能是把輸入的64位資料塊按位重新組合，並把輸出分為L0、R0兩部分，每部分各長32位，其置換規則為將輸入的第58位換到第一位,第50位換到第2位……依此類推,最後一位是原來的第7位。L0、R0則是換位輸出後的兩部分，L0是輸出的左32位，R0是右32位,例:設定換前的輸入值為D1D2D3……D64,則經過初始置換後的結果為:L0=D58D50……D8;R0=D57D49……D7。

經過16次迭代運算後,得到L16、R16,將此作為輸入，進行逆置換，逆置換正好是初始置換的逆運算，由此即得到密文輸出。

此演算法是對稱加密演算法體系中的代表,在計算機網路系統中廣泛使用。

(2) AES：高階加密標準(英語：Advanced Encryption Standard，縮寫：AES)，在密碼學中又稱Rijndael加密法，是美國聯邦政府採用的一種區塊加密標準。這個標準用來替代原先的DES，已經被多方分析且廣為全世界所使用。經過五年的甄選流程，高階加密標準由美國國家標準與技術研究院(NIST)於2001年11月26日釋出於FIPS PUB 197，並在2002年5月26日成為有效的標準。2006年，高階加密標準已然成為對稱金鑰加密中最流行的演算法之一。

AddRoundKey — 矩陣中的每一個位元組都與該次輪祕鑰(round key)做XOR運算;每個子金鑰由金鑰生成方案產生。

SubBytes — 通過非線性的替換函式，用查詢表的方式把每個位元組替換成對應的位元組。

ShiftRows — 將矩陣中的每個橫列進行迴圈式移位。

MixColumns — 為了充分混合矩陣中各個直行的操作。這個步驟使用線性轉換來混合每列的四個位元組。

2. 非對稱演算法

非對稱金鑰也叫公開金鑰加密,它是用兩個數學相關的金鑰對資訊進行編碼。在此係統中，其中一個金鑰叫公開金鑰，可隨意發給期望同金鑰持有者進行安全通訊的人。公開金鑰用於對資訊加密。第二個金鑰是私有金鑰，屬於金鑰持有者，此人要仔細儲存私有金鑰。金鑰持有者用私有金鑰對收到的資訊進行解密。

(1) RSA：RSA演算法基於一個十分簡單的數論事實：將兩個大質數相乘十分容易，但是想要對其乘積進行因式分解卻極其困難，因此可以將乘積公開作為加密金鑰。

因為兩個大素數的乘積因式分解時，除了1和其本身(這兩個不在分解範圍內)外，只有這兩個大素數，但是分解時不知道這兩個大素數，只有從最小的素數2開始，逐步試除，直到這兩個大素數中較小的一個，當然非常困難了。

在公開金鑰密碼體制中，加密金鑰(即公開金鑰)PK是公開資訊，而解密金鑰(即祕密金鑰)SK是需要保密的。加密演算法E和解密演算法D也都是公開的。雖然解密金鑰SK是由公開金鑰PK決定的，但卻不能根據PK計算出SK。

RSA演算法是一種非對稱密碼演算法，所謂非對稱，就是指該演算法需要一對金鑰，使用其中一個加密，則需要用另一個才能解密。

RSA的演算法涉及三個引數，n、e1、e2。

其中，n是兩個大質數p、q的積，n的二進位制表示時所佔用的位數，就是所謂的金鑰長度。

e1和e2是一對相關的值，e1可以任意取，但要求e1與(p-1)(q-1)互質;再選擇e2，要求(e2e1)mod((p-1)*(q-1))=1。

(n，e1),(n，e2)就是金鑰對。其中(n，e1)為公鑰，(n，e2)為私鑰。

RSA加解密的演算法完全相同，設A為明文，B為密文，則：A=B^e2 mod n;B=A^e1 mod n;(公鑰加密體制中，一般用公鑰加密，私鑰解密)

e1和e2可以互換使用，即：

A=B^e1 mod n；B=A^e2 mod n;

3. 雜湊演算法

雜湊演算法將任意長度的二進位制值對映為較短的固定長度的二進位制值，這個小的二進位制值稱為雜湊值。雜湊值是一段資料唯一且極其緊湊的數值表示形式。如果雜湊一段明文而且哪怕只更改該段落的一個字母，隨後的雜湊都將產生不同的值。要找到雜湊為同一個值的兩個不同的輸入，在計算上是不可能的，所以資料的雜湊值可以檢驗資料的完整性。一般用於快速查詢和加密演算法。簡單解釋：雜湊(Hash)演算法,即雜湊函式。它是一種單向密碼體制,即它是一個從明文到密文的不可逆的對映,只有加密過程,沒有解密過程。同時,雜湊函式可以將任意長度的輸入經過變化以後得到固定長度的輸出。雜湊函式的這種單向特徵和輸出資料長度固定的特徵使得它可以生成訊息或者資料。

(1) MD5：MD5即Message-Digest Algorithm 5(資訊-摘要演算法5)，用於確保資訊傳輸完整一致。是計算機廣泛使用的雜湊演算法之一(又譯摘要演算法、雜湊演算法)，主流程式語言普遍已有MD5實現。將資料(如漢字)運算為另一固定長度值，是雜湊演算法的基礎原理，MD5的前身有MD2、MD3和MD4。

MD5演算法具有以下特點：

壓縮性：任意長度的資料，算出的MD5值長度都是固定的。

容易計算：從原資料計算出MD5值很容易。

抗修改性：對原資料進行任何改動，哪怕只修改1個位元組，所得到的MD5值都有很大區別。

強抗碰撞：已知原資料和其MD5值，想找到一個具有相同MD5值的資料(即偽造資料)是非常困難的。

(2) 2SHA-256：安全雜湊演算法256位。SHA-1安全性比MD5稍高(160位VS128位)，但演算法需要時間SHA-1稍慢。

五、 密碼分析詳解

密碼編碼學的主要目的是保持明文(或者是金鑰)的祕密並防止竊聽者(也可以叫對手、攻擊者、擷取者、入侵者、敵人等)知曉。這裡假設竊聽者完全能夠截獲傳送者和接收者之間的通訊。

密碼分析學是在不知道金鑰的情況下，恢復明文的科學。成功的密碼分析可以恢復訊息的明文或者金鑰。與此同時，密碼分析也可以驗證出密碼體制的弱點，並最終恢復明文或者金鑰。

對密碼進行分析的嘗試稱為攻擊(attack)。A.Kerckhoffs 早在19世紀就闡明瞭密碼分析的一個基本假設，此假設就是祕密必須全寓於金鑰中。Kerckhoffs假設密碼分析者已知密碼演算法以及其實現的全部資料。雖然在實際的密碼分析中並不總是擁有如此詳細的資訊，但理應如此假設。這樣如果不能破譯演算法，那麼即便了解演算法是如何工作的也是徒然。當然，如果連演算法的知識和相關資料都沒有，那就肯定無法破譯。

現我列出常用的七類密碼分析攻擊，在此假設每一類密碼分析者都知道所用的加密演算法的全部知識。

唯密文攻擊(ciphertext-only attack)。密碼分析者有一些訊息的密文，這些訊息都用相同的加密演算法進行加密。密碼分析者的任務就是恢復儘可能多的明文，或者最好能推算出加密訊息的金鑰，以便可採用相同的金鑰破解其他被加密的訊息。

已知明文攻擊(known-plaintext attack)。密碼分析者不僅可得到一些訊息的密文，而且也知道這些訊息的明文。分析者的任務就是用加密資訊推出用來加密的金鑰或匯出一個演算法，此演算法可以對用相同金鑰加密的任何新訊息進行解密。

選擇明文攻擊(chosen-plaintext attack)。分析者不僅可以得到一些訊息的密文和相同的明文，而且還可以選擇被加密的明文。這比已知明文攻擊更加有效，因為密碼分析者能選擇特定的明文塊進行加密，那些塊可能產生更多關於金鑰的資訊。分析者的任務就是推匯出用來加密訊息的金鑰或匯出一個演算法，此演算法可以對用相同金鑰加密的任何新訊息進行解密。

自適應選擇明文攻擊(adaptive-chosen-plaintext attack)。這是選擇明文攻擊的特殊情況。密碼分析者不僅能夠選擇被加密的明文，還可以基於以前加密的結果修正這個選擇。在選擇明文攻擊中，密碼分析者還可以選擇一大塊被加密的明文。而在自適應選擇明文攻擊中，可以選擇較小的明文塊，然後再基於第一塊的結果選擇另一個明文塊，以此類推。

選擇密文攻擊(chosen-ciphertext attack)。密碼分析者能選擇不同的被加密的密文，並可得到對應的解密的明文。例如，密碼分析者訪問一個防篡改的自動解密盒，密碼分析者的任務就是推匯出金鑰。

選擇金鑰攻擊(chosen-key attack)。這種攻擊並不表示密碼分析者能夠選擇金鑰，其只是表示密碼分析者具有不同金鑰之間關係的有關知識。

軟磨硬泡攻擊(rubber-hose cryptanalysis)。密碼分析者威脅、勒索，或者通過折磨某人，直到其給出金鑰為止。通過行賄獲取金鑰的方法，有時稱為購買金鑰攻擊(purchase-key attack)。這些是非常有效的攻擊，並經常是破譯演算法的最便捷途徑。