每天一道LeetCode-----買賣商品問題,計算最大利潤,分別有一次交易,兩次交易,多次交易的情況
Best Time to Buy and Sell Stock
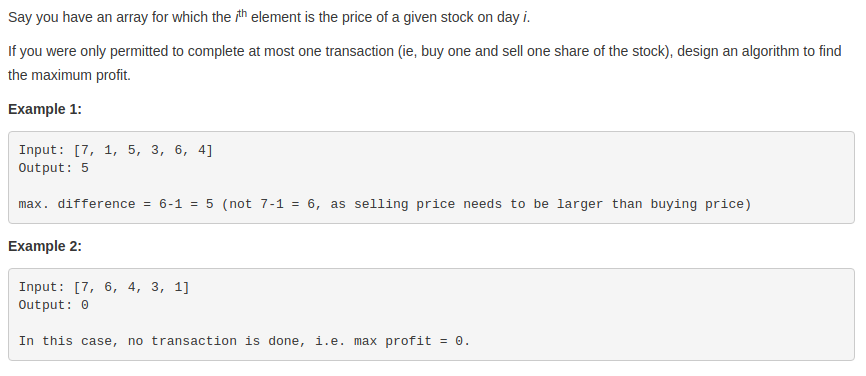
給定一個價格序列prices,其中prices[i]代表第i天商品的價格,商家需要在某一天買入,然後在之後的某一天出售,計算可以獲得的最大利潤
本質就是計算
假設已經直到最後結果的最大值位置i(prices[i]),只需要減去最小值即可,那麼就需要直到最小值是多少,本題中當從左到右遍歷時,完全可以隨著遍歷進度的增加記錄最小值
程式碼如下
class Solution {
public:
int maxProfit(vector<int
當然也可以遍歷兩次求解,第一次對於每個位置的值,計算它的右側比它大的最大值,第二次對於每個位置,計算右側的最大值與自己的差,更新最大差值,求出結果
程式碼如下
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector Best Time to Buy and Sell Stock II

要求和上面一樣,不過這次可以進行多次交易,即買,賣,買,賣,買,賣…,其中買賣不能在同一天進行
這樣就不能像上面那樣只求一次了,其實仔細想一下,序列無非三種排列
- 遞增,假設
A<B<C<D - 遞減,假設
A>B>C>D - 無序,假設
A<B>C<D
對於遞增序列,最大的差值就是
對於遞減序列,為0
對於無序序列,總可以找到若干個遞增序列,就上面的例子而言最大差值為
所以只要依次計算
程式碼如下
class Solution {
public:
int maxProfit(vector<int>& prices) {
int maxProfit = 0;
for(int i = 1; i < prices.size(); ++i)
maxProfit += std::max(prices[i] - prices[i - 1], 0);
return maxProfit;
}
};Best Time to Buy and Sell Stock III

同樣是買賣問題,本題要求最多可以完成兩次交易,計算最大利潤
利用動態規劃,對動態規劃陣列states[i][j]有如下規定
- states[][0]代表0次買,0次賣的利潤
- states[][1]代表一次買,0次賣的利潤(顯然是負數)
- states[][2]代表一次買,一次賣的利潤
- states[][3]代表兩次買,一次賣的利潤
- states[][4]代表兩次買,兩次賣的利潤
而states,規定它是二維陣列,states[0]代表當前的利潤,states[1]代表執行完本次操作後的利潤,那麼有
- states[1][1] = std::max(states[0][1], states[0][0] - prices[i]),表示買入商品prices[i],那麼利潤就是0次買0次賣的利潤減商品價格,當然需要和1次買0次賣比較,選擇較大的那個
- states[1][2] = std::max(states[0][2], states[0][1] + prices[i]),表示賣出商品prices[i],那麼利潤就是1次買0次賣的利潤加商品價格,當然需要和1次買1次賣比較,選擇較大的那個
- …同理
初始狀態,另1次買0次賣的利潤為INT_MIN,兩次買一次賣的利潤為INT_INT,是為了讓max選擇後者,因為初始狀態沒有買入任何商品
程式碼如下
class Solution {
public:
int maxProfit(vector<int>& prices) {
vector<vector<int>> states(2, vector<int>(2 * 2 + 1, 0));
states[0][0] = 0;
for(int i = 1; i < 2 * 2 + 1; i += 2)
{
states[0][i] = INT_MIN;
states[0][i + 1] = 0;
}
int cur = 0, next = 1;
for(int i = 0; i < prices.size(); ++i)
{
states[next][1] = std::max(states[cur][1], states[cur][0] - prices[i]);
states[next][2] = std::max(states[cur][2], states[cur][1] + prices[i]);
states[next][3] = std::max(states[cur][3], states[cur][2] - prices[i]);
states[next][4] = std::max(states[cur][4], states[cur][3] + prices[i]);
/* next變為當前 */
std::swap(next, cur);
}
return states[cur][2 * 2];
}
};Best Time to Buy and Sell Stock IV

和上面一樣,要求最多可以進行k次交易
只需要將上面的兩次交易換成k次即可
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
vector<vector<int>> states(2, vector<int>(2 * k + 1, 0));
states[0][0] = 0;
for(int i = 1; i < 2 * k + 1; i += 2)
{
states[0][i] = INT_MIN;
states[0][i + 1] = 0;
}
int cur = 0, next = 1;
for(int i = 1; i < prices.size(); ++i)
{
/* 把兩次變為k次,就需要放在迴圈裡了 */
for(int j = 1; j < 2 * k + 1; j += 2)
{
states[next][j] = std::max(states[cur][j], states[cur][j - 1] - prices[i]);
states[next][j + 1] = std::max(states[cur][j + 1], states[cur][j] + prices[i]);
}
std::swap(next, cur);
}
return states[cur][2 * k];
}
};不過這樣可能記憶體溢位,因為如果k很大,申請的記憶體很容易溢位,解決方法是當k很大時採用其他方法。什麼時候k算大呢,就是k次交易可以涉及到每一天,也就是k >= prices.size() / 2,此時就可以轉換為沒有交易次數限制的問題
程式碼如下
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
/* 如果k很大,採用其他方式 */
if(k >= prices.size() / 2)
return quickSolver(prices);
vector<vector<int>> states(2, vector<int>(2 * k + 1, 0));
for(int i = 1; i < 2 * k + 1; i += 2)
{
states[0][i] = INT_MIN;
states[0][i + 1] = 0;
}
int cur = 0, next = 1;
for(int i = 0; i < prices.size(); ++i)
{
/* 把兩次變為k次,就需要放在迴圈裡了 */
for(int j = 1; j < 2 * k + 1; j += 2)
{
states[next][j] = std::max(states[cur][j], states[cur][j - 1] - prices[i]);
states[next][j + 1] = std::max(states[cur][j + 1], states[cur][j] + prices[i]);
}
std::swap(next, cur);
}
return states[cur][2 * k];
}
private:
/* 沒有交易次數限制,直接遍歷,見第二題 */
int quickSolver(vector<int>& prices)
{
int profit = 0;
for(int i = 1; i < prices.size(); ++i)
profit += std::max(prices[i] - prices[i - 1], 0);
return profit;
}
};第一道題的第一種解法比較好,直接遍歷一遍同時記錄最小值和最大差值,同時也沒有額外的空間使用
第二道題不太容易理解,其實對於序列無非遞增,遞減,無序三種可能,分別觀察一下即可
第三第四題主要以動態規劃為主
