我們瞭解下從二分衍生出來的三分法
摘自hihocoder（略改）：
當函式是凸形函式時，二分法就無法適用，這時就需要用到三分法。
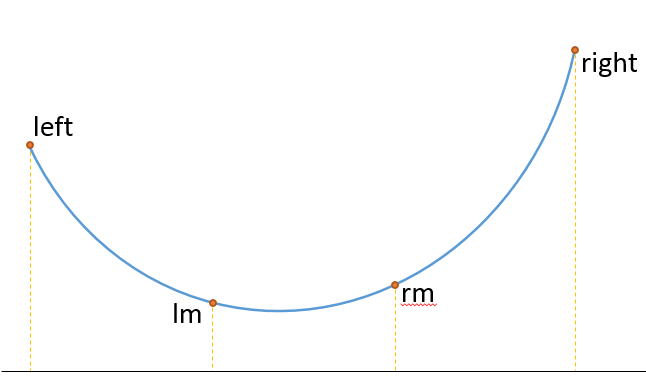
從三分法的名字中我們可以猜到，三分法是對於需要逼近的區間做三等分：

如圖這種情況先減後增，適用於求答案的極小值，若lm比rm低（即lm對應的函式值 < rm函式值）則極小點（圖中最低點）肯定在[ left, rm ] ，反之在[ lm, right ]，剩下就跟二分一樣根據大小關係調整區間就行了。

double solve(double l,double r)
{
    while(fabs(r-l) > esp)
    {
        double lmid = l + (r-l)/3
 
,rmid = r - (r-l)/3;
        if(val(lmid) >= val(rmid))  //求極大值
        /*if(val(lmid) <= val(rmid))    //求極小值 */
            r = rmid;
        else
            l = lmid;
    }
    return val(l);
}