題意：

n*m的矩形，每個格子上有一個數字代表顏色，有q次詢問，問(1,l),(n,r)這兩個點對應的矩形的連通塊有多少個。

1<n<10, 1<m<100000

解題思路 :

這題最麻煩的就是寫合併了，然後也是讓我對並查集又重新認識了一下。。

只要往線段樹那個方向想了,想到每個區間維護左右兩個列應該不難，然後再想一想這個題目要求連通塊個數，那麼應該也能想到左右兩個列應該是並查集。

然後需要注意的是L（左邊的列）陣列和R陣列不是單獨的列上的並查集，而是從l到r上的整個區間的並查集的一部分，有什麼區別呢？

如圖

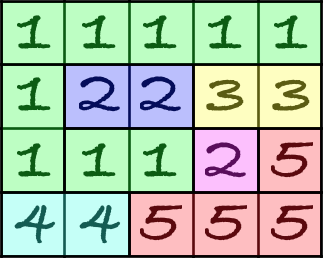
第二列裡(1,2)和(3,2)顏色相同，如果是單獨的列的話，他們不屬於同一個祖先，如果是[1,2]整個區間上的並查集的話，(1,2)和(3,2)是屬於同一個祖先的,這兩者是有區別的。

合併的時候就是cnt=lson.cnt+rson.cnt，然後兩個區間中間兩列的並查集每合併一次，cnt--，最後cnt就是這個區間的連通數量了。

然後上面提到的那個區別為什麼呢？

假如(2,4)和(3,4)也是1的話，區間[1,2]和區間[3,4]合併的時候如果2,3列的並查集只是單獨自己列上的並查集的話，cnt需要減2次，而實際上應該只減1次，所以應該維護的是整個區間的並查集。

然後學到了把並查集下標和值同時+2*n這種操作。

需要注意的是並查集數組裡的值也就是那幾個祖先的範圍和下標的範圍也該是一樣的，合併操作最後得到的兩個並查集需要重新賦值。（看程式碼就知道了）

程式碼：

#include <bits/stdc++.h>
#define lson o<<1
#define rson o<<1|1
#define ps push_back
using namespace std;
const int maxn=1e5+5;
int n, m, q;
int a[11][maxn];

struct p
{
    int l, r;
    int c[22];
    int x;
    void init()
    {
        x=0;

        return;
    }
}val[maxn<<2];
vector<int>tmp[11*4];
int f[44];
int getf(int x)
{
    if(x==f[x])return x;
    else return f[x]=getf(f[x]);
}
int merg(int x, int y)
{
    int a=getf(x), b=getf(y);
    if(a>b)swap(a,b);
    if(a!=b)
    {
        f[b]=a;
        return 1;
    }
    else return 0;
}

void init(int n)
{
    for(int i=1; i<=n; i++)f[i]=i;
    return;
}

p operator + (const  p &A, const  p &B)
{
    p res;
    res.l=A.l, res.r=B.r;
    res.x=A.x+B.x;
    for(int i=1; i<=2*n; i++)
    {
        f[i]=A.c[i];
        f[i+2*n]=B.c[i]+2*n;
    }
    for(int i=1; i<=n; i++)
    {
        if(a[i][A.r]==a[i][B.l])
        {
            res.x-=merg(i+2*n, i+n);
        }
    }


    for(int i=1; i<=4*n; i++)tmp[i].clear();
    for(int i=1; i<=n; i++)
    {
        tmp[getf(i)].ps(i);
        tmp[getf(i+3*n)].ps(i+n);
    }
    for(int i=1; i<=4*n; i++)
    {
        for(int j=0; j<(int)tmp[i].size(); j++)
        {
            res.c[tmp[i][j]]=tmp[i][0]; //重新賦值，使祖先的範圍和下標的範圍對應
        }
    }
    
    return res;
}



void build(int o, int l, int r)
{
    val[o].l=l, val[o].r=r;
    if(l==r)
    {
        val[o].x=n;
        init(n);
        for(int i=2; i<=n; i++)
        {
            if(a[i][l]==a[i-1][l])
            {
                val[o].x-=merg(i, i-1);
            }
        }

        for(int i=1; i<=n; i++)
        {
            val[o].c[i]=val[o].c[i+n]=getf(i);
        }

        return;
    }
    int mid=(l+r)>>1;
    
    build(lson, l, mid);
    build(rson, mid+1, r);
    val[o]=val[lson]+val[rson];

    return;

}

p query(int o, int l, int r, int ll, int rr)
{
    if(l==ll && r==rr)
    {
        return val[o];
    }
    int mid=(l+r)>>1;
    if(rr<=mid)return query(lson, l, mid, ll, rr);

    if(ll>mid)return query(rson, mid+1, r, ll, rr);

    return query(lson, l, mid, ll, mid)+query(rson, mid+1, r, mid+1, rr);    
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);
    int i, j, k, x, y;
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=m; j++)
        {
            scanf("%d", &a[i][j]);
        }
    }

    build(1, 1, m);

    int l, r;
    while(q--)
    {
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, 1, m, l, r).x);
    }

}