關於圖的幾個概念定義：

• 連通圖：在無向圖中，若任意兩個頂點vi與vj都有路徑相通，則稱該無向圖為連通圖。
• 強連通圖：在有向圖中，若任意兩個頂點vi與vj都有路徑相通，則稱該有向圖為強連通圖。
• 連通網：在連通圖中，若圖的邊具有一定的意義，每一條邊都對應著一個數，稱為權；權代表著連線連個頂點的代價，稱這種連通圖叫做連通網。
• 生成樹：一個連通圖的生成樹是指一個連通子圖，它含有圖中全部n個頂點，但只有足以構成一棵樹的n-1條邊。一顆有n個頂點的生成樹有且僅有n-1條邊，如果生成樹中再新增一條邊，則必定成環。
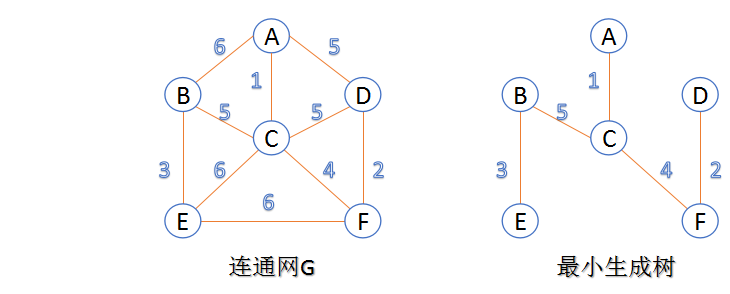
• 最小生成樹：在連通網的所有生成樹中，所有邊的代價和最小的生成樹，稱為最小生成樹。
  

下面介紹兩種求最小生成樹演算法

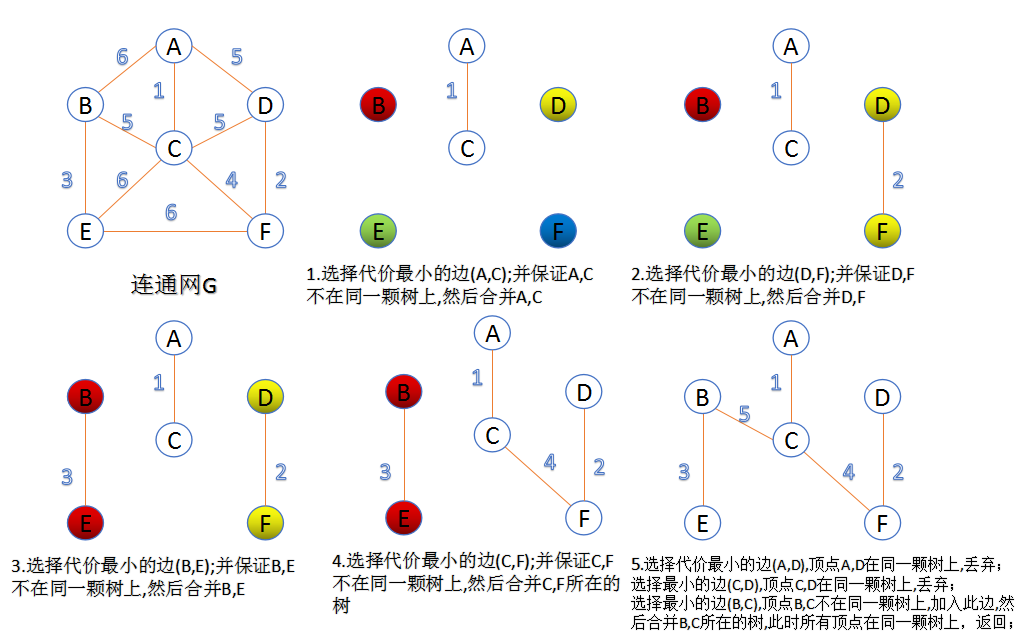
1.Kruskal演算法

此演算法可以稱為“加邊法”，初始最小生成樹邊數為0，每迭代一次就選擇一條滿足條件的最小代價邊，加入到最小生成樹的邊集合裡。
1. 把圖中的所有邊按代價從小到大排序；
2. 把圖中的n個頂點看成獨立的n棵樹組成的森林；
3. 按權值從小到大選擇邊，所選的邊連線的兩個頂點ui,vi,應屬於兩顆不同的樹，則成為最小生成樹的一條邊，並將這兩顆樹合併作為一顆樹。
4. 重複(3),直到所有頂點都在一顆樹內或者有n-1條邊為止。

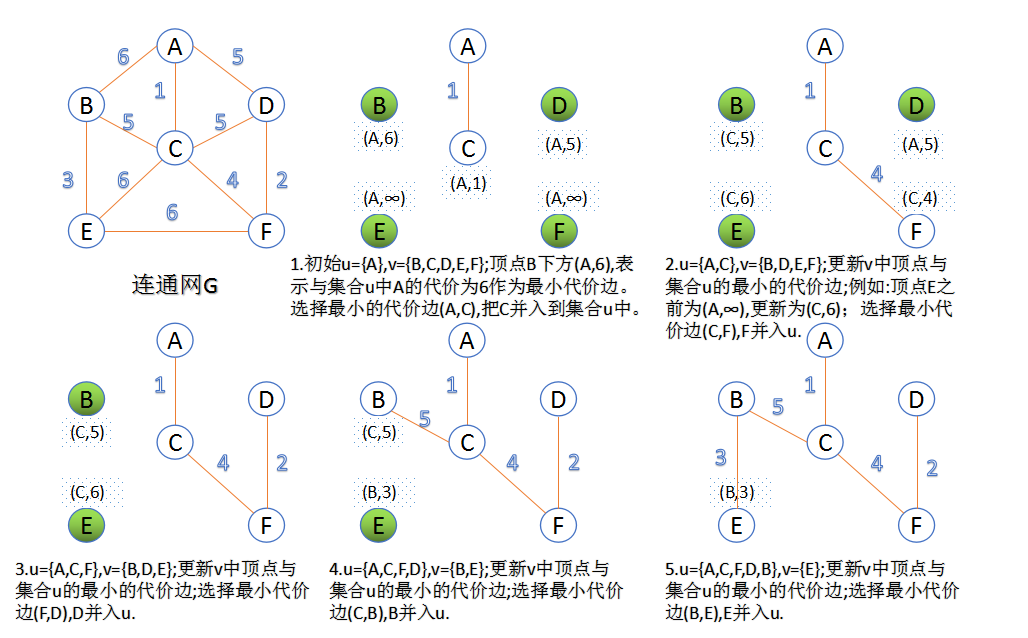
2.Prim演算法

此演算法可以稱為“加點法”，每次迭代選擇代價最小的邊對應的點，加入到最小生成樹中。演算法從某一個頂點s開始，逐漸長大覆蓋整個連通網的所有頂點。

1. 圖的所有頂點集合為V；初始令集合u={s},v=V−u;
2. 在兩個集合u,v能夠組成的邊中，選擇一條代價最小的邊(u0,v0)，加入到最小生成樹中，並把v0併入到集合u中。
3. 重複上述步驟，直到最小生成樹有n-1條邊或者n個頂點為止。

由於不斷向集合u中加點，所以最小代價邊必須同步更新；需要建立一個輔助陣列closedge,用來維護集合v中每個頂點與集合u中最小代價邊資訊，：

struct
{
  char vertexData   //表示u中頂點資訊
  UINT lowestcost   //最小代價
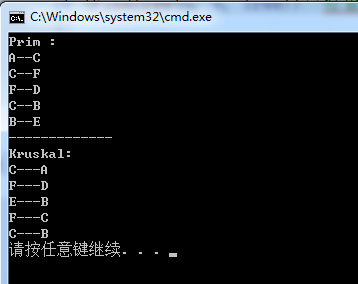
}closedge[vexCounts]

3.完整程式碼

/************************************************************************
CSDN 勿在浮沙築高臺 http://blog.csdn.net/luoshixian099演算法導論--最小生成樹（Prim、Kruskal）2016年7月14日
************************************************************************/
 

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INFINITE 0xFFFFFFFF   
#define VertexData unsigned int  //頂點資料
#define UINT  unsigned int
#define vexCounts 6  //頂點數量
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node 
{
    VertexData data;
    unsigned int lowestcost;
}closedge[vexCounts]; //Prim演算法中的輔助資訊
typedef struct 
{
    VertexData u;
    VertexData v;
    unsigned int cost;  //邊的代價
}Arc;  //原始圖的邊資訊
void AdjMatrix(unsigned int adjMat[][vexCounts])  //鄰接矩陣表示法
{
    for (int i = 0; i < vexCounts; i++)   //初始化鄰接矩陣
        for (int j = 0; j < vexCounts; j++)
        {
            adjMat[i][j] = INFINITE;
        }
    adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge)  //返回最小代價邊
{
    unsigned int min = INFINITE;
    int index = -1;
    for (int i = 0; i < vexCounts;i++)
    {
        if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
        {
            min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
    for (int i = 0; i < vexCounts;i++)
    {
        closedge[i].lowestcost = INFINITE;
    }      
    closedge[s].data = s;      //從頂點s開始
    closedge[s].lowestcost = 0;
    for (int i = 0; i < vexCounts;i++)  //初始化輔助陣列
    {
        if (i != s)
        {
            closedge[i].data = s;
            closedge[i].lowestcost = adjMat[s][i];
        }
    }
    for (int e = 1; e <= vexCounts -1; e++)  //n-1條邊時退出
    {
        int k = Minmum(closedge);  //選擇最小代價邊
        cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成樹
        closedge[k].lowestcost = 0; //代價置為0
        for (int i = 0; i < vexCounts;i++)  //更新v中頂點最小代價邊資訊
        {
            if ( adjMat[k][i] < closedge[i].lowestcost)
            {
                closedge[i].data = k;
                closedge[i].lowestcost = adjMat[k][i];
            }
        }
    }
}
void ReadArc(unsigned int  adjMat[][vexCounts],vector<Arc> &vertexArc) //儲存圖的邊代價資訊
{
    Arc * temp = NULL;
    for (unsigned int i = 0; i < vexCounts;i++)
    {
        for (unsigned int j = 0; j < i; j++)
        {
            if (adjMat[i][j]!=INFINITE)
            {
                temp = new Arc;
                temp->u = i;
                temp->v = j;
                temp->cost = adjMat[i][j];
                vertexArc.push_back(*temp);
            }
        }
    }
}
bool compare(Arc  A, Arc  B)
{
    return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //檢查u,v分別屬於哪顆樹
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }

    if (index_u != index_v)   //u,v不在一顆樹上，合併兩顆樹
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
    vector<Arc> vertexArc;
    ReadArc(adjMat, vertexArc);//讀取邊資訊
    sort(vertexArc.begin(), vertexArc.end(), compare);//邊按從小到大排序
    vector<vector<VertexData> > Tree(vexCounts); //6棵獨立樹
    for (unsigned int i = 0; i < vexCounts; i++)
    {
        Tree[i].push_back(i);  //初始化6棵獨立樹的資訊
    }
    for (unsigned int i = 0; i < vertexArc.size(); i++)//依次從小到大取最小代價邊
    {
        VertexData u = vertexArc[i].u;  
        VertexData v = vertexArc[i].v;
        if (FindTree(u, v, Tree))//檢查此邊的兩個頂點是否在一顆樹內
        {
            cout << vextex[u] << "---" << vextex[v] << endl;//把此邊加入到最小生成樹中
        }   
    }
}

int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);   //鄰接矩陣
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0); //Prim演算法，從頂點0開始.
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal演算法
    return 0;
}

Reference:
資料結構–耿國華
演算法導論–第三版