二叉樹的三種非遞迴遍歷和層次遍歷
阿新 • • 發佈:2018-12-24
1 .三種非遞迴遍歷(棧)
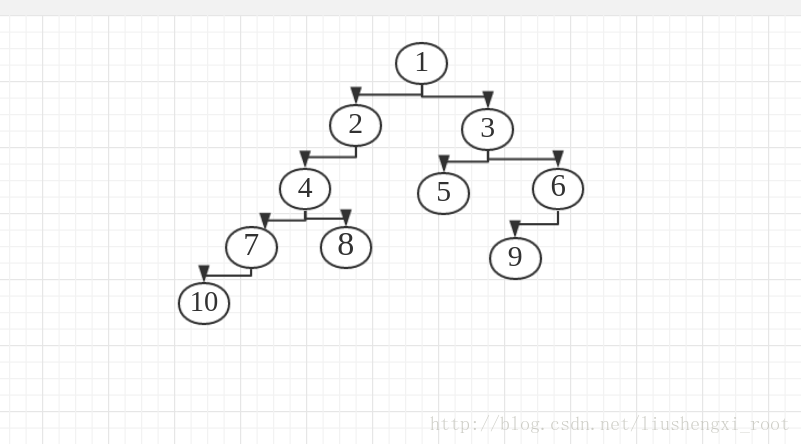
所要遍歷的樹是:
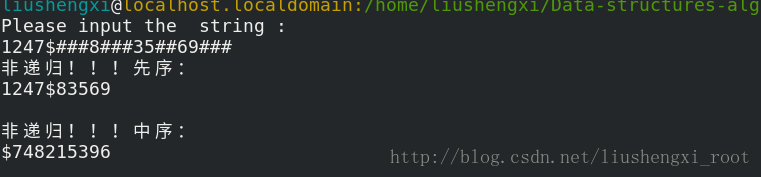
先序 + 中序
思路:就拿先序遍歷為例來說吧。
1.訪問根節點,根節點入棧,進入左子樹。
2.訪問左子樹的根節點,根節點入棧,進入下一層左子樹。
3.重複直到當前節點為空。即到達了最**左下方**的節點
4.如果棧不為空,就從棧頂取出節點,進入其右子樹
5.直到當前節點和棧都為空時,結束。(棧為空就是所有的入棧的節點的右子樹都訪問過了。當前節點為空就代表所有的節點都訪問過了)
實現程式碼:
#include<iostream>
using namespace std 執行截圖:
後序
思路:後序的遍歷要比前面的兩種複雜一些。因為在前面我們的思路就是進左子樹,然後從左子樹返回,退棧,進右子樹。而在後序中,我們是必須先訪問完左右子樹才能退棧,訪問根節點。那麼我們如何知道是從哪個子樹返回的吶?其實也很簡單的啦。就設定一個標記(tag),左為0,右為1。如果tag==1就退棧返回,如果不為1,就修改它的tag==1,繼續壓回去,往右子樹走就行了
實現程式碼:
#include<iostream>
using namespace std;
typedef struct Node {
char data ;
struct Node * Lchild ;
struct Node * Rchild ;
}BiNode ;
typedef struct temp{
BiNode *ptr;
int tag ;
struct temp *next ;
}SeqStack;
void CreteBitree(BiNode **root)
{
char ch ;
cin >> ch ;
if( ch == '#' )
*root= NULL;
else {
*root = (BiNode *)malloc(sizeof(BiNode));
(*root)->data = ch;
CreteBitree(&(*root)->Lchild);
CreteBitree(&(*root)->Rchild);
}
}
void InitSeqStack(SeqStack **S) //開始建立連結串列 ,S 就是頭節點
{
*S = (SeqStack *)malloc(sizeof(SeqStack));
(*S)->next = NULL ;
}
void Push(SeqStack *S,SeqStack p)
{
SeqStack *temp ;
temp=(SeqStack *)malloc(sizeof(SeqStack));
temp->tag = p.tag ;
temp->ptr = p.ptr ;
temp->next = S->next ;
S->next = temp ;
}
SeqStack Pop(SeqStack *S ,SeqStack p)
{
SeqStack *t ;
t= S->next ;
p.ptr = t->ptr ;
p.tag = t->tag ;
S->next = t->next ;
free(t);
return p ;
}
int IsEmpty(SeqStack *S)
{
if(S->next == NULL )
return 1;
else return 0;
}
void PostOrder_with_stack(BiNode *root)
{
SeqStack *S;
SeqStack p ;
InitSeqStack(&S);
p.ptr = root ;
while(p.ptr != NULL || !IsEmpty(S) )
{
while(p.ptr != NULL )
{
//入棧
p.tag= 0 ;
Push(S,p);
p.ptr=p.ptr->Lchild;
}
if(!IsEmpty(S))
{
p=Pop(S,p);
//cout << "3333333" << endl ;
if(p.tag == 0 ){
p.tag = 1;
Push(S,p);
p.ptr=p.ptr->Rchild;
}
else{
cout << p.ptr->data ;
p.ptr = NULL ; // 思考一下這是為什麼??
}
}
}
cout << endl ;
}
int main(void)
{
BiNode *root;
cout << "Please input the string :" << endl ;
CreteBitree(&root);
cout << "非遞迴!!!後序遍歷:" << endl;
PostOrder_with_stack(root);
return 0;
}執行截圖:
總結:三種不同的遍歷過程的搜尋路徑是相同的,不同的僅是三次經過節點時哪一次訪問節點。但無論那次經過節點訪問時,在第一次經過節點時,都需要保留其節點資訊。以便返回時,找到其右子樹或者該節點。
2.層次遍歷(佇列+BFS)
思路:先訪問的節點的其孩子也將先訪問,後訪問的節點的其孩子也將後訪問,先進先出與佇列的形式相同哦
1.隊頭節點出隊,並訪問出隊節點
2.出隊節點的左右孩子依次入隊
實現程式碼:
#include<iostream>
using namespace std;
typedef struct Node {
char data ;
struct Node * Lchild ;
struct Node * Rchild ;
}BiNode ;
typedef struct t1{
BiNode *ptr ;
struct t1 *next ;
}Queue;
typedef struct t2{
Queue *front;
Queue *rear;
}LinkList_Queue;
void CreteBitree(BiNode **root)
{
char ch ;
cin >> ch ;
if( ch == '#' )
*root= NULL;
else {
*root = (BiNode *)malloc(sizeof(BiNode));
(*root)->data = ch;
CreteBitree(&(*root)->Lchild);
CreteBitree(&(*root)->Rchild);
}
}
void InitQueue(LinkList_Queue **Q)
{
*Q =(LinkList_Queue *)malloc(sizeof(LinkList_Queue)) ;
(*Q)->front = (*Q)->rear = (Queue *)malloc(sizeof(Queue));
(*Q)->front->next = NULL;
}
void InQueue(LinkList_Queue *Q ,BiNode *p)
{
Queue *temp ;
temp = (Queue *)malloc(sizeof(Queue));
temp->ptr = p ;
temp->next = Q->rear->next ; //尾插
Q->rear->next = temp ;
Q->rear = temp ;
}
void OutQueue(LinkList_Queue *Q,BiNode **p) //賦值給p ,頭取
{
Queue *temp ;
temp = Q->front->next;
(*p) = Q->front->next->ptr ;
Q->front->next = temp->next ;
if(Q->front->next == NULL ) //一個元素時,需要修改尾指標 !!!!
Q->front = Q->rear ;
}
int IsEmpyt(LinkList_Queue *Q)
{
if(Q->front == Q->rear )
return 1;
else return 0;
}
void LevelOrder(BiNode *root) //層次遍歷
{
LinkList_Queue *Q;
BiNode *p;
InitQueue(&Q);
InQueue(Q,root);
while( !IsEmpyt(Q))
{
OutQueue(Q,&p); //p 是 BiNode 型的,Q 是LinkList_Queue 型的
cout << p->data << " ";
if(p->Lchild != NULL )
InQueue(Q,p->Lchild);
if(p->Rchild != NULL)
InQueue(Q,p->Rchild);
}
cout << endl ;
}
int main(void)
{
BiNode *root;
cout << "Please input the string :" << endl ;
CreteBitree(&root);
cout << "層次遍歷:" << endl ;
LevelOrder(root);
cout << endl;
return 0;
}