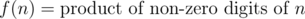
Let us define two functions f and g on positive integer numbers.

                                                               

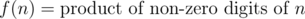
You need to process Q queries. In each query, you will be given three integers l, r and k. You need to print the number of integers xbetween l and r inclusive, such that g(x

The first line of the input contains an integer Q (1 ≤ Q ≤ 2 × 105) representing the number of queries.

Q lines follow, each of which contains 3 integers l, r and k (1 ≤ l ≤ r ≤ 106, 1 ≤ k ≤ 9).

For each query, print a single line containing the answer for that query.

4
22 73 9
45 64 6
47 55 7
2 62 4

1
4
0
8

4
82 94 6
56 67 4
28 59 9
39 74 4

3
1
1
5

題意：f(n)函式功能：求出n的各數位的乘積，同時自動忽略0，例如f(102)=2，即f(n) !=0，g(n)題意已明確。現在給你一個區間l,r，一個數字k，問你區間l,r內的數字i有幾個g(i)=k。

思路：區間大小1e6，k只有9個，所以字首和打表即可。

時間複雜度：字首和打表+線上查詢=O(1e6*9)+O(1e5*2)。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int ans[10][1000005],q,l,r,k;
int op(int x)         //f(n)函式的功能實現
{
    if(x<10)return x;
    int tmp,as;
    while(1)
    {
        as=1;
        while(x)
        {
            tmp=x%10;
            x/=10;
            if(tmp)as*=tmp;
        }
        if(as<10)return as;
        x=as;
    }
}
int main()
{
    for(int i=1;i<=9;i++)ans[i][0]=0;
    for(int i=1;i<=9;i++)              //字首和打表
    {
        for(int j=1;j<=1000000;j++)
        {
            if(op(j)==i){ans[i][j]=ans[i][j-1]+1;}
            else ans[i][j]=ans[i][j-1];
        }
    }
    scanf("%d",&q);
    while(q--)         //線上查詢
    {
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",ans[k][r]-ans[k][l-1]);
    }
    return 0;
}