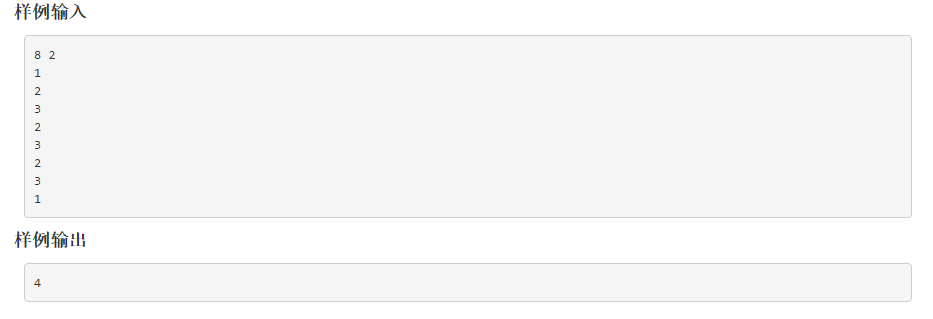
字尾陣列(一)——hiho120最長可重疊重複K次子串
本人閱讀hihocoder題目及講解後整理此文章
題目分析
這個問題稱為“最長可重疊重複K次子串問題”,所求的是符合要求的所有子串的長度的最大值,這個要求是:子串在字串中重複出現過至少K次,其中子串可以(部分)重疊。
原文解題方法提示中給出瞭解決方法,使用字尾陣列suffix和一個height陣列,並且這兩個陣列都有高效的求解演算法。
字尾陣列suffix和height陣列
字尾陣列:記錄所有後綴的陣列,並且有序。可用於解決單字串問題、兩個字串的問題和多個字串的問題。
e.g. 字串banana$,($表示字串結尾),suffix(p)表示從原字串第p個字元開始到字串結尾的字尾(字尾p),rank[p]表示字尾 p在所有後綴中從小到大排列的“名次”,排好序的陣列記為sa
| b | a | n | a | n | a | $ |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| i | 字尾 suffix(p) | sa[i]=p | rank[p] | height[i] |
|---|---|---|---|---|
| 1 | $ | 7 | rank[7]=1 | x |
| 2 | a$ | 6 | rank[6]=2 | 0 |
| 3 | ana$ | 4 | rank[4]=3 | 1 |
| 4 | anana$ | 2 | rank[2]=4 | 3 |
| 5 | banana$ | 1 | rank[1]=5 | 0 |
| 6 | na$ | 5 | rank[5]=6 | 0 |
| 7 | nana$ | 3 | rank[3]=7 | 2 |
height陣列:令 height[i] 是 suffix(sa[i-1]) 和 suffix(sa[i]) 的最長公共字首長度,即排名相鄰的兩個字尾的最長公共字首長度。比如height[4]就是anana$和ana$的最長公共字首,也就是ana,長度為3。height也附在上表中.
heigh陣列有兩個性質,這對於優化height的計算非常有用。
- 若 rank[j] < rank[k],則字尾 Sj..n 和 Sk..n 的最長公共字首為
min{height[rank[j]+1],height[rank[j]+2]…height[rank[k]]}。
這個性質是顯然的,因為我們已經字尾按字典序排列。 - height[rank[i]] ≥ height[rank[i-1]]-1
選定一個字尾suffix(i-1),它前一個字尾記為suffix(k),則它們的最長公共字首是height[rank[i-1]]。
①若height[rank[i-1]] ≤ 1,則height[rank[i-1]]-1 ≤ 1 - 1 = 0 ≤
height[rank[i]]。
②若 height[rank[i-1]] >1,那麼suffix(k+1)將排在suffix(i)的前面,height[rank[i-1]]至少為2,那麼suffix(k),suffix(i-1)至少前2個字母是一樣的,從第三個字母開始符合字典序,那麼suffix(k+1),suffix(i),至少前1個字母是一樣的,後面符合字典序,也就是說suffix(k+1)將排在suffix(i)的前面,而且二者的最長公共字首是height[rank[i-1]]-1。所以suffix(i)和在它前一名的字尾的最長公共字首至少是height[rank[i-1]]-1(suffix(k+1)和suffix(i)之間可能有其他的字尾,只能使得公共字首更大或一樣)
問題轉化
題目要求最長可重疊重複K次子串,有height陣列這個問題方便很多。
重複子串即兩字尾的公共字首,最長重複子串,等價於兩字尾的最長公共字首的最大值.(最長公共字首一定是從相鄰的字尾中取得)
求最長可重疊重複K次子串轉化為求height 陣列中最大的長度為 K的子序列的最小值
原文“小Hi:哈哈!厲害!轉化後的這個問題對我來說太容易了,利用單調佇列或者二分都可以輕鬆搞定。”
字尾陣列的求解
如果對字尾陣列排序,字串長度為N,陣列有N項,使用快排平均要O(N*lgN)次比較,字串比較時間不是常數,是O(N),總體複雜度為O(N*N*lgN),N較大時方法不使用,倍增演算法複雜度是O(N*lgN),DC3的複雜度是O(N)
字尾陣列的求法有很多,最有名的是兩種倍增演算法和DC演算法。DC演算法時間複雜度更優,但更復雜,倍增演算法較實用。
倍增演算法思想是:先求出字尾的k-字首的rank值,然後根據這個值對2k-字首按照雙關鍵字進行基數排序
倍增演算法的步驟:
對長度為 2^0=1 的字串,也就是所有單字母排序。
用長度為 2^0=1 的字串,對長度為 2^1=2 的字串進行雙關鍵字排序。考慮到時間效率,我們一般用基數排序。
用長度為 2^(k-1( 的字串,對長度為 2^k 的字串進行雙關鍵字排序。
直到 2^k ≥ n,或者名次陣列 Rank 已經從 1 排到 n,得到最終的字尾陣列。
height陣列的求解
height[rank[i]] ≥ height[rank[i-1]]-1
按照 height[rank[1]], height[rank[2]] … height[rank[n]] 的順序計算,利用height陣列的性質,就可以將時間複雜度可以降為 O(n)。這是因為height陣列的值最多不超過n,每次計算結束我們只會減1,所以總的運算不會超過2n次。
面向過程風格實現
void solve()
{
for (int i = 0; i < 256; i ++) cntA[i] = 0;
for (int i = 1; i <= n; i ++) cntA[ch[i]] ++;
for (int i = 1; i < 256; i ++) cntA[i] += cntA[i - 1];
for (int i = n; i; i --) sa[cntA[ch[i]] --] = i;
rank[sa[1]] = 1;
for (int i = 2; i <= n; i ++)
{
rank[sa[i]] = rank[sa[i - 1]];
if (ch[sa[i]] != ch[sa[i - 1]]) rank[sa[i]] ++;
}
for (int l = 1; rank[sa[n]] < n; l <<= 1)
{
for (int i = 0; i <= n; i ++) cntA[i] = 0;
for (int i = 0; i <= n; i ++) cntB[i] = 0;
for (int i = 1; i <= n; i ++)
{
cntA[A[i] = rank[i]] ++;
cntB[B[i] = (i + l <= n) ? rank[i + l] : 0] ++;
}
for (int i = 1; i <= n; i ++) cntB[i] += cntB[i - 1];
for (int i = n; i; i --) tsa[cntB[B[i]] --] = i;
for (int i = 1; i <= n; i ++) cntA[i] += cntA[i - 1];
for (int i = n; i; i --) sa[cntA[A[tsa[i]]] --] = tsa[i];
rank[sa[1]] = 1;
for (int i = 2; i <= n; i ++)
{
rank[sa[i]] = rank[sa[i - 1]];
if (A[sa[i]] != A[sa[i - 1]] || B[sa[i]] != B[sa[i - 1]]) rank[sa[i]] ++;
}
}
for (int i = 1, j = 0; i <= n; i ++)
{
if (j) j --;
while (ch[i + j] == ch[sa[rank[i] - 1] + j]) j ++;
height[rank[i]] = j;
}
} 面向物件風格實現
Suffix Array using Prefix Doubling Algorithm
* see also: Udi Manber and Gene Myers' seminal paper(1991): "Suffix arrays: A new method for on-line string searches"
*
* Copyright (c) 2011 ljs (http://blog.csdn.net/ljsspace/)
* Licensed under GPL (http://www.opensource.org/licenses/gpl-license.php)
*
* @author ljs
* 2011-07-17
*
*/
public class PrefixDoubling {
public static final char MAX_CHAR = '\u00FF';
class Suffix{
int[] sa;
//Note: the p-th suffix in sa: SA[rank[p]-1]];
//p is the index of the array "rank", start with 0;
//a text S's p-th suffix is S[p..n], n=S.length-1.
int[] rank;
boolean done;
}
//a prefix of suffix[isuffix] represented with digits
class Tuple{
int isuffix; //the p-th suffix
int[] digits;
public Tuple(int suffix,int[] digits){
this.isuffix = suffix;
this.digits = digits;
}
public String toString(){
StringBuffer sb = new StringBuffer();
sb.append(isuffix);
sb.append("(");
for(int i=0;i<digits.length;i++){
sb.append(digits[i]);
if(i<digits.length-1)
sb.append("-");
}
sb.append(")");
return sb.toString();
}
}
//the plain counting sort algorithm for comparison
//A: input array
//B: output array (sorted)
//max: A value's range is 0...max
public void countingSort(int[] A,int[] B,int max){
//init the counter array
int[] C = new int[max+1];
for(int i=0;i<=max;i++){
C[i] = 0;
}
//stat the count in A
for(int j=0;j<A.length;j++){
C[A[j]]++;
}
//process the counter array C
for(int i=1;i<=max;i++){
C[i]+=C[i-1];
}
//distribute the values in A to array B
for(int j=A.length-1;j>=0;j--){
//C[A[j]] <= A.length
B[--C[A[j]]]=A[j];
}
}
//d: the digit to do countingsort
//max: A value's range is 0...max
private void countingSort(int d,Tuple[] tA,Tuple[] tB,int max){
//init the counter array
int[] C = new int[max+1];
for(int i=0;i<=max;i++){
C[i] = 0;
}
//stat the count
for(int j=0;j<tA.length;j++){
C[tA[j].digits[d]]++;
}
//process the counter array C
for(int i=1;i<=max;i++){
C[i]+=C[i-1];
}
//distribute the values
for(int j=tA.length-1;j>=0;j--){
//C[A[j]] <= A.length
tB[--C[tA[j].digits[d]]]=tA[j];
}
}
//tA: input
//tB: output for rank caculation
private void radixSort(Tuple[] tA,Tuple[] tB,int max,int digitsLen){
int len = tA.length;
int digitsTotalLen = tA[0].digits.length;
for(int d=digitsTotalLen-1,j=0;j<digitsLen;d--,j++){
this.countingSort(d, tA, tB, max);
//assign tB to tA
if(j<digitsLen-1){
for(int i=0;i<len;i++){
tA[i] = tB[i];
}
}
}
}
//max is the maximum value in any digit of TA.digits[], used for counting sort
//tA: input
//tB: the place holder, reused between iterations
private Suffix rank(Tuple[] tA,Tuple[] tB,int max,int digitsLen){
int len = tA.length;
radixSort(tA,tB,max,digitsLen);
int digitsTotalLen = tA[0].digits.length;
//caculate rank and sa
int[] sa = new int[len];
sa[0] = tB[0].isuffix;
int[] rank = new int[len];
int r = 1; //rank starts with 1
rank[tB[0].isuffix] = r;
for(int i=1;i<len;i++){
sa[i] = tB[i].isuffix;
boolean equalLast = true;
for(int j=digitsTotalLen-digitsLen;j<digitsTotalLen;j++){
if(tB[i].digits[j]!=tB[i-1].digits[j]){
equalLast = false;
break;
}
}
if(!equalLast){
r++;
}
rank[tB[i].isuffix] = r;
}
Suffix suffix = new Suffix();
suffix.rank= rank;
suffix.sa = sa;
//judge if we are done
if(r==len){
suffix.done = true;
}else{
suffix.done = false;
}
return suffix;
}
//Precondition: the last char in text must be less than other chars.
public Suffix solve(String text){
if(text == null)return null;
int len = text.length();
if(len == 0) return null;
int k=1;
char base = text.charAt(len-1); //the smallest char
Tuple[] tA = new Tuple[len];
Tuple[] tB = new Tuple[len]; //placeholder
for(int i=0;i<len;i++){
tA[i] = new Tuple(i,new int[]{0,text.charAt(i)-base});
}
Suffix suffix = rank(tA,tB,MAX_CHAR-base,1);
while(!suffix.done){ //no need to decide if: k<=len
k<<=1;
int offset = k>>1;
for(int i=0,j=i+offset;i<len;i++,j++){
tA[i].isuffix = i;
tA[i].digits=new int[]{suffix.rank[i],
(j<len)?suffix.rank[i+offset]:0};
}
int max = suffix.rank[suffix.sa[len-1]];
suffix = rank(tA,tB,max,2);
}
return suffix;
}
public void report(Suffix suffix){
int[] sa = suffix.sa;
int[] rank = suffix.rank;
int len = sa.length;
System.out.println("suffix array:");
for(int i=0;i<len;i++){
System.out.format(" %s", sa[i]);
}
System.out.println();
System.out.println("rank array:");
for(int i=0;i<len;i++){
System.out.format(" %s", rank[i]);
}
System.out.println();
}
public static void main(String[] args){
/*
//plain counting sort test:
int[] A= {2,5,3,0,2,3,0,3};
PrefixDoubling pd = new PrefixDoubling();
int[] B = new int[A.length];
pd.countingSort(A,B,5);
for(int i=0;i<B.length;i++)
System.out.format(" %d", B[i]);
System.out.println();
*/
String text = "GACCCACCACC#";
PrefixDoubling pd = new PrefixDoubling();
Suffix suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "mississippi#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "abcdefghijklmmnopqrstuvwxyz#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "yabbadabbado#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
System.out.println("********************************");
text = "DFDLKJLJldfasdlfjasdfkldjasfldafjdajfdsfjalkdsfaewefsdafdsfa#";
pd = new PrefixDoubling();
suffix = pd.solve(text);
System.out.format("Text: %s%n",text);
pd.report(suffix);
}
}解題程式碼
略