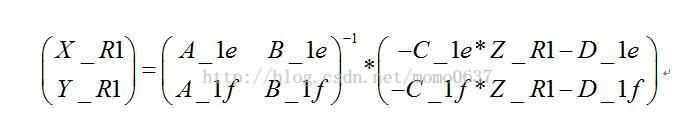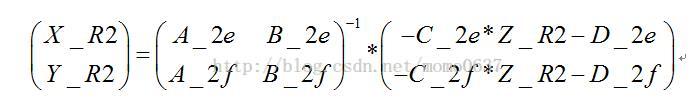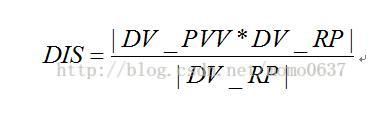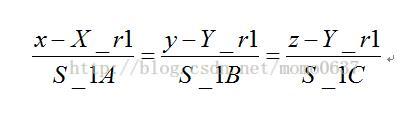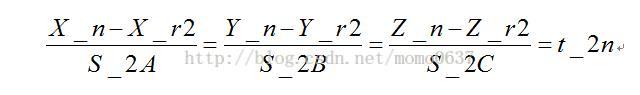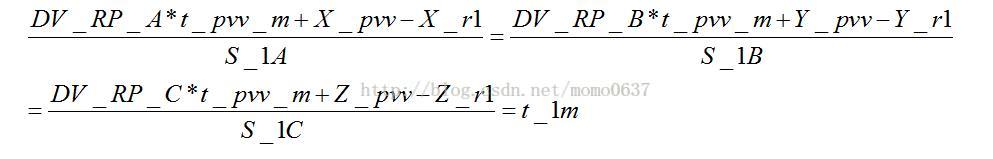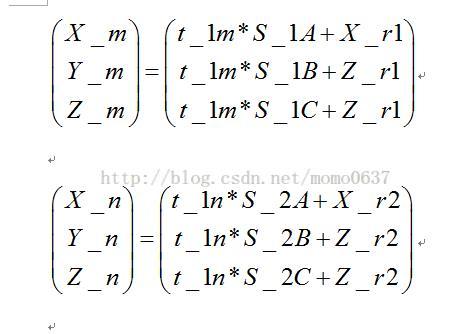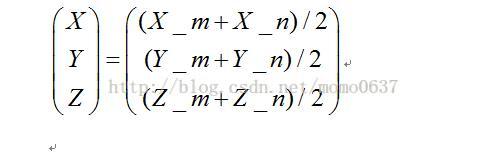未經許可請勿轉載


在雙目視覺立體空間重建中，會根據兩個相機中的物體影象座標，求取給定三維座標系的三維座標，而可以根據物體
影象座標、相機內參、給定座標系的相機外參，求取相機光軸線的方程，從而實現立體重建，內外參、直線方程請執行
搜尋學習，本文主要是解決在已知空間兩直線求最短距離及最近點。如有疑問或錯誤，請與評論區指出，謝謝。
一、理論：
已知空間中兩線段，如果它們無限變粗，判斷是否相交。（主要討論不在同一平面的情況）
線段AB，線段CD
問題的關鍵是求出這兩條任意直線之間的最短距離，以及在這個距離上的兩線最接近點座標，判斷該點是否線上段AB
和線段CD上。
首先將直線方程化為對稱式，得到其方向向量n1=（a1,b1,c1),n2=(a2,b2,c2).
再將兩向量叉乘得到其公垂向量N=（x,y,z）,在兩直線上分別選取點A,B(任意)，得到向量AB，
求向量AB在向量N方向的投影即為兩異面直線間的距離了（就是最短距離了）。
最短距離的求法：d=|向量N*向量AB|/|向量N|（上面是兩向量的數量積，下面是取模）。
設交點為C,D，帶入公垂線N的對稱式中，又因為C,D兩點分別滿足一開始的直線方程，所以得到關於C（或D）的兩個
連等方程，分別解出來就好了！
二、方程式
直線1：(平面式)
面e:A_1e*x+B_1e*y+C_1e*z+D_1e=0;
面f:A_1f*x+B_1f*y+C_1f*z+D_1f=0;
 
直線2：（平面式）
面e:A_2e*x+B_2e*y+C_2e*z+D_2e=0;
面f:A_2f*x+B_2f*y+C_2f*z+D_2f=0;
 
直線1的方向向量：（direction vector）
DV_1=(A_1e,B_1e,C_1e)X(A_1f,B_1f,C_1f)
=(B_1e*C_1f-B_1f*C_1e, C_1f*A_1e-A_1e*C_1f,A_1e*B_1f-A_1f*B_1e);
DV_2=(B_2e*C_2f-B_2f*C_2e, C_2f*A_2e-A_2e*C_2f,A_2e*B_2f-A_2f*B_2e);
 
在直線1、2上任取一點R1，R2






領Z_R1=1,Z_R2=1;
直線1帶入Z_R 1有：
面e:A_1e*x+B_1e*y+C_1e*Z_R1+D_1e=0;
面f:A_1f*x+B_1f*y+C_1f*Z_R1+D_1f=0;

即：

P_R1=(X_R1,Y_R1,Z_R1);
 
同理：

P_R2=(X_R2,Y_R2,Z_R2);
 
兩條直線的公垂線：（public vertical vector）
DV_PVV=(DV_1) X( DV_2);
在兩條直線任意選的點的方向向量：


DV_RP=(P_R1-P_R2);
 
任選直線的方向向量與公垂線向量的數量積：即此直線在公垂線上的投影(d=|n*AB|/|N|):

當DIS小於某個給定閾值時，求最近點。

直線1的對稱性方程：

令公垂線與直線1交於點m,交線與點n;
有

直線2：

並且把m、n帶入公垂線方程，有：

把用公垂線表示的點m和n,分別帶入直線1和2的對稱性方程,消除點m和n, 有：
直線1:

直線2：

上述兩式相減：

 
求出t_1m,t_2n,則m和n

最近點：

#include<opencv2/core/core.hpp>
using namespace cv;
Point3d two_space_linear_collision_get_nearest_point(double A_0e, double B_0e, double C_0e, double D_0e, double A_0f, double B_0f, double C_0f, double D_0f,
double A_1e, double B_1e, double C_1e, double D_1e, double A_1f, double B_1f, double C_1f, double D_1f)
{
//直線0的A面的D,A,B,C
double line0_flatE_d = D_0e;


Mat line0_flatE = (Mat_<double>(1, 3) << A_0e, B_0e, C_0e);


//直線0的B面的D,A,B,C
double line0_flatF_d = D_0f;
Mat line0_flatF = (Mat_<double>(1, 3) << A_0f, B_0f, C_0f);


//直線1的A面的D,A,B,C
double line1_flatE_d = D_1e;
Mat line1_flatE = (Mat_<double>(1, 3) << A_1e, B_1e, C_1e);


//直線1的B面的D,A,B,C
double line1_flatF_d = D_1f;
Mat line1_flatF = (Mat_<double>(1, 3) << A_1f, B_1f, C_1f);




//兩條直線0，1的direction vector（raws = 1, cols = 3）
Mat direction_line0 = line0_flatE.cross(line0_flatF);


Mat direction_line1 = line1_flatE.cross(line1_flatF);


//line0的randpoint
Point3d randPoint0(0.0, 0.0, 0.0);
randPoint0.z = 800;
Mat randPoint0_in = (Mat_<double>(2, 2) << line0_flatE.at<double>(0, 0), line0_flatE.at<double>(0, 1),
line0_flatF.at<double>(0, 0), line0_flatF.at<double>(0, 1));


Mat randPoint0_out = randPoint0_in.inv()*(Mat_<double>(2, 1) << -line0_flatE_d - randPoint0.z*line0_flatE.at<double>(0, 2),
-line0_flatF_d - randPoint0.z*line0_flatF.at<double>(0, 2));
randPoint0.x = randPoint0_out.at<double>(0, 0);
randPoint0.y = randPoint0_out.at<double>(1, 0);




//line1上randpoint
Point3d randPoint1(0.0, 0.0, 0.0);
randPoint1.z = 800;
Mat randPoint1_in = (Mat_<double>(2, 2) << line1_flatE.at<double>(0, 0), line1_flatE.at<double>(0, 1),
line1_flatF.at<double>(0, 0), line1_flatF.at<double>(0, 1));


Mat randPoint1_out = randPoint1_in.inv()*(Mat_<double>(2, 1) << -line1_flatE_d - randPoint1.z*line1_flatE.at<double>(0, 2),
-line1_flatF_d - randPoint1.z*line1_flatF.at<double>(0, 2));
randPoint1.x = randPoint1_out.at<double>(0, 0);
randPoint1.y = randPoint1_out.at<double>(1, 0);


//Public vertical vector(rows=1,cols=3)
Mat publicVerticalRay = direction_line0.cross(direction_line1);




//任選點的方向向量
Mat randRay = (Mat_<double>(3, 1) << randPoint0.x - randPoint1.x, randPoint0.y - randPoint1.y, randPoint0.z - randPoint1.z);


Mat cross_rand_mult = publicVerticalRay*randRay;


//公垂線的模
double public_vertical_vector_length = sqrtf(publicVerticalRay.at<double>(0, 0)*publicVerticalRay.at<double>(0, 0)
+ publicVerticalRay.at<double>(0, 1)*publicVerticalRay.at<double>(0, 1)
+ publicVerticalRay.at<double>(0, 2)*publicVerticalRay.at<double>(0, 2));


//兩直線的最小距離d=|公向量*任選向量|/|公向量|
double minDistance = std::abs(cross_rand_mult.at<double>(0, 0)) / public_vertical_vector_length;


Point3d point_3d(0.0,0.0,0.0);


if (minDistance<50)
{


Mat two_line_t_in = (Mat_<double>(3, 3) << publicVerticalRay.at<double>(0, 0), -direction_line0.at<double>(0, 0), direction_line1.at<double>(0, 0),
publicVerticalRay.at<double>(0, 1), -direction_line0.at<double>(0, 1), direction_line1.at<double>(0, 1),
publicVerticalRay.at<double>(0, 2), -direction_line0.at<double>(0, 2), direction_line1.at<double>(0, 2));


Mat two_line_t = two_line_t_in.inv()*randRay;


Point3d node0, node1;


node0.x = two_line_t.at<double>(1, 0)*direction_line0.at<double>(0, 0) + randPoint0.x;
node0.y = two_line_t.at<double>(1, 0)*direction_line0.at<double>(0, 1) + randPoint0.y;
node0.z = two_line_t.at<double>(1, 0)*direction_line0.at<double>(0, 2) + randPoint0.z;


node1.x = two_line_t.at<double>(2, 0)*direction_line1.at<double>(0, 0) + randPoint1.x;
node1.y = two_line_t.at<double>(2, 0)*direction_line1.at<double>(0, 1) + randPoint1.y;
node1.z = two_line_t.at<double>(2, 0)*direction_line1.at<double>(0, 2) + randPoint1.z;


point_3d = (node0 + node1) / 2;

}
else
{
point_3d = Point3d(0.0,0.0,0.0);
}


return point_3d;


}
 

Have a good day~

注：編寫比較匆忙，如有偏差請諒解，未經許可請勿轉載