Mishka and Game

題目連結：

解題思路：

In this problem you had to do use the following algo. If Mishka wins Chris in the current round, then increase variable countM by 1. Otherwise (if Chris wins Mishka) increase variable countC. After that you had to compare this values and print the answer.

AC程式碼：

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n;
    while(~scanf("%d",&n)){
        int cnt1 = 0,cnt2 = 0;
        int x,y;
        for(int i = 0; i < n; ++i){
            scanf("%d%d",&x,&y);
            if(x > y)
                ++cnt1;
            else if(x < y)
                ++cnt2;
        }
        if(cnt1 > cnt2)
            puts("Mishka");
        else if(cnt1 < cnt2)
            puts("Chris");
        else
            puts("Friendship is magic!^^");
    }
    return 0;
}
 

Mishka and trip

題目連結：

解題思路：

Let's look at the first capital. Note that the total cost of the outgoing roads is c[id1] · (sum - c[id1]), where sum — summary beauty of allcities. Thus iterating through the capitals we can count the summary cost of roads between capitals and all the other cities. But don't forget that in this case we count the roads between pairs of capitals twice. To avoid this on each step we should update sum

Complexity — O(n).

演算法思想：

題解是O（nlogn）的，其實我們只需要求出字首和，然後先求出每個首都城市x，對答案的貢獻：c[x] * others即可。O（n）.

AC程式碼：

#include <bits/stdc++.h>
using namespace std;

typedef long long int ll;
const int N = 100005;
int c[N];
bool vis[N];

int main(){
    int n,k;
	while(~scanf("%d%d",&n,&k)){
        memset(vis,false,sizeof(vis));
        ll sum = 0;
        for(int i = 1; i <= n; ++i){
            scanf("%d",&c[i]);
            sum += c[i];
        }
        ll visc = 0,ans = 0;
        for(int i = 1; i <= k; ++i){
            int x;
            scanf("%d",&x);
            visc += c[x];
            ans += c[x]*(sum-visc);
            vis[x] = true;
        }
        for(int i = 1; i <= n; ++i){
            if(vis[i] || vis[i+1])
                continue;
            ans += c[i]*c[i+1];
        }
        if(!vis[1] && !vis[n])
            ans += c[1]*c[n];
        printf("%lld\n",ans);
	}
	return 0;
}
 

Chris and Road

題目連結：

解題思路：

Imagine that the bus stands still and we move "to the right" with a constant speed v. Then it's not hard to see that movement along the liney = (u / v) · (x  -  t0) is optimal, where t0 — time in which we begin our movement. In this way answer is t = t0 + (w / u).

If t0 = 0, then we start our movement immediately. In this case we need to check that our line doesn't intersect polygon (either we can cross the road in front of a bus, or the bus is gone).

Otherwise we need to find such minimal t0 that our line is tangent to the polygon. It can be done with binary search.

Complexity — O(n log n).

我們可以先考慮人直接過去，而車撞不到人的情況；然後再考慮人等車先過，人再過的情況即可。

AC程式碼：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 10005;
int n,w,v,u;
int x[N],y[N];

bool pre(){
    for(int i = 0; i < n; ++i)
        if(ll(x[i])*u < ll(y[i])*v)
            return false;
    return true;
}

double solve(){
    double ret = w*1.0/u;
    for(int i = 0; i < n; ++i)
        ret = max(ret, x[i]*1.0/v + (w-y[i])*1.0/u);
    return ret;
}

int main(){
    while(~scanf("%d%d%d%d",&n,&w,&v,&u)){
        for(int i = 0; i < n; i++)
            scanf("%d%d",&x[i],&y[i]);
        if(pre()){
            printf("%.6lf\n",w*1.0/u);
            return 0;
        }
        printf("%.6lf\n",solve());
    }
    return 0;
}

Mishka and Interesting sum

題目連結：

解題思路：

Easy to see, that the answer for query is XOR-sum of all elements in the segment xored with XOR-sum of distinct elements in the segment. XOR-sum of all numbers we can find in O(1) using partial sums. As for the XOR-sum of distinct numbers... Let's solve easier problem.

Let the queries be like "find the number of distinct values in a segment". Let's sort all the queries according to their right bounds and iterate through all elements of our array. We also need to make a list last, where last[value] is the last position of value on the processed prefix of array. Assume we are at position r. Then the answer for the query in the segment [l,  r] (l ≤ r) is 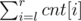, where cnt[i] = 1 iflast[ai] = i and 0 otherwise. It's easy to store and update such values in cnt. When moving to the next position we have to make the following assignments: cnt[last[ai]] = 0, cnt[i] = 1, last[ai] = i. To get described sum in O(log n) we can use segment tree (or Fenwick tree) instead of standard array.

Now let's turn back to our problem. Everything we have to do is to change assignment cnt[i] = 1 to cnt[i] = ai and count XOR-sum instead of sum. Now we can solve this problem in O(n log n).

題目大意：

給你n個數，然後m次查詢，每一次查詢輸出所在給定區間內出現偶數次數的數的異或值，如果只有一個出現偶數次數的數，則直接

輸出該數，如果沒有出現偶數次數的數，則直接輸出0。

和求一個區間內不同元素個數的做法一樣。樹狀陣列存的是不同元素的字首異或和。用map標記數a[i]最近的出現的下標。其實就是

先求出這個區間的（異或和），然後再異或上這個區間不同數的異或和（即由樹狀陣列來完成的）。

AC程式碼：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 1000005;
map<int,int> mp;
vector<int> que[N];
int n,m;
int a[N];
int l[N],r[N];
ll res[N],bit[N];
ll ans[N];

int lowbit(int x){
    return x&(-x);
}

void update(int x, ll val){
	for(int i = x; i <= n; i += lowbit(i))
		bit[i] ^= val;
}

int sum(int x){
	ll res = 0;
	for(int i = x; i > 0; i -= lowbit(i))
		res ^= bit[i];
	return res;
}

int main(){
	while(~scanf("%d",&n)){
        mp.clear();
        memset(res,0,sizeof(res));
        for(int i = 0; i <= n; ++i)
            que[i].clear();
        for(int i = 1; i <= n; ++i){
            scanf("%d",&a[i]);
            res[i] = (res[i-1]^a[i]);
        }
        scanf("%d",&m);
        for(int i = 0; i < m; ++i){
            scanf("%d%d",&l[i],&r[i]);
            que[l[i]].push_back(i);
            ans[i] = res[r[i]]^res[l[i]-1];
        }
        for(int i = n; i >= 1; --i){
            int x = a[i];
            if(mp.count(x))
                update(mp[x],x);
            update(i,x);
            mp[x] = i;
            for(int j = 0; j < que[i].size(); ++j){
                int id = que[i][j];
                ans[id] ^= sum(r[id]);
            }
        }
        for(int i = 0; i < m; ++i)
            printf("%lld\n", ans[i]);
	}
	return 0;
}