【譯】Relational inductive biases, deep learning, and graph network(未完成)
關係歸納偏置、深度學習、圖網路
摘要
人工智慧(AI)最近經歷了一次復興,在視覺、語言、控制和決策等關鍵領域取得了重大進展。這在一定程度上要歸因於廉價的資料和廉價的計算資源,因為這些資源符合深度學習的自然優勢。然而,在不同的壓力下發展起來的人類智力的許多決定性特徵,仍然是當前方法無法實現的。特別是,超越個人經驗的概括——從嬰兒時期開始的人類智慧的標誌——仍然是現代人工智慧的一項艱鉅挑戰。
以下是部分工作研究,部分回顧和部分統一。我們認為組合泛化必須是AI實現類似人類能力的首要任務,結構化表示和計算是實現這一目標的關鍵。就像生物學使用自然和培養合作一樣,我們拒絕“手工工程”和“端到端”學習之間的錯誤選擇,而是倡導一種從其互補優勢中獲益的方法。我們探索如何在深度學習架構中使用關係歸納偏差來促進對實體,關係和組成它們的規則的學習。我們為AI工具包提供了一個新的構建模組,具有強大的關係歸納偏差 - 圖網路 - 它概括泛化和擴充套件了在圖形上執行的神經網路的各種方法,併為操縱結構化知識和生成結構化行為提供了直接的介面。我們討論圖網路如何支援關係推理和組合泛化,為更復雜,可解釋和靈活的推理模式奠定基礎。
1 引言
人類智慧的一個關鍵特徵是能夠“無限地使用有限的方法”(Humboldt,1836; Chomsky,1965),其中一小部分元素(如文字)可以以無限的方式有效地組合在一起(例如,組成新句子)。這反映了組合泛化的原則,即從已知構建塊構建新的推論,預測和行為。在這裡,我們探討如何通過將學習偏向於結構化表示和計算,特別是在圖上執行的系統來提高現代AI的組合泛化能力。
人類組合泛化的能力,在很大程度上取決於我們表達關係結構和推理關係的認知機制。我們將複雜系統表示為實體及其相互作用的組合(Navon,1977; McClelland and Rumelhart,1981; Plaut et al.,1996; Marcus,2001; Goodwin and Johnson-Laird,2005; Kemp and Tenenbaum,2008),如判斷一個不規則物體的堆疊是否穩定(Battaglia et al.,2013)。我們使用層次結構來抽象出細微差異,並捕捉表徵和行為之間更普遍的共性(Botvinick,2008; Tenenbaum et al.,2011),例如一個物體的一部分,一個場景中的物體,一個城鎮中的社群,和一個國家中的城鎮。我們通過撰寫熟悉的技能和慣例來解決新問題(Anderson,1982),例如通過編寫熟悉的程式和目標去一個新的地點旅行,例如“乘飛機旅行”,“飛往聖地亞哥”,“在那吃飯”,以及“一家印度餐館”。我們通過對齊兩個域之間的關係結構來繪製類比,並基於對另一個域的相應知識得出關於一個域的推論(Gentner and Markman,1997; Hummel and Holyoak,2003)。
Kenneth Craik的“解釋的本質”(1943)將世界的構成結構與我們內在心理模型的組織方式聯絡起來:
…[人類心智模型]與其模仿的過程具有相似的關係結構。我所使用的“關係 - 結構”,並不是指某個模糊的非物理實體會出現在模型中,而是說它是一個可以工作的物理模型,其工作方式與它所對應的過程是一樣的…構建了物理現實,顯然,從一些基本型別的單位屬性確定的許多屬性最複雜的現象,這似乎是對這些組合之間關係結構的機制和相似性之間類比的出現的充分解釋,而這些組合沒有任何客觀共性理論的必要性(Craik,1943,第51-55頁)。
也就是說,世界是組合而成的,或者至少我們在構成方面可以這麼理解它。 在學習時,我們要麼將新知識應用到我們現有的結構化表示中,要麼調整結構本身以更好地適應(和利用)新舊結構(Tenenbaum et al.,2006; Griffiths et al.,2010; Ullman et al.,2017)。
如何建立展示組合泛化的人工系統的問題一直是人工智慧的核心,並且是許多結構化方法的核心,包括邏輯,語法,經典規劃,圖形模型,因果推理,貝葉斯非引數和概率規劃(Chomsky,1957; Nilsson and Fikes,1970; Pearl,1986,2009; Russell and Norvig,2009; Hjort et al.,2010; Goodman et al.,2012; Ghahramani,2015)。整個子領域都側重於以現實的實體和關係為中心的學習,例如關係增強學習(Dzeroski et al.,2001)和統計關係學習(Getoor and Taskar,2007)。結構化方法在以前的時代對機器學習如此重要的一個關鍵原因,部分是因為資料和計算資源很昂貴,並且結構化方法強大的歸納偏差對改進樣本複雜性是非常有價值的。
與過去的人工智慧方法相比,現代深度學習方法(LeCun et al.,2015; Schmidhuber,2015; Goodfellowet al.,2016)經常遵循“端到端”設計理念,強調最小的先驗表徵和計算假設,並試圖避免顯式結構和“手工工程”。這種強調更適合由當前豐富的廉價資料和廉價計算資源,這使得用樣本效率更靈活的學習成為一種理性的選擇。從影象分類(Krizhevsky et al. ,2012; Szegedy et al.,2017)到許多具有挑戰性的領域的顯著和快速進展,關於自然語言處理(Sutskever et al.,2014; Bahdanau et al.,2015),到玩遊戲(Mnih et al.,2015; Silver et al.,2016;Moravc’ık et al.,2017),這些證明了這種極簡主義原則。一個突出的例子來自語言翻譯,其中不使用顯式的解析樹或語言實體之間的複雜關係,從序列到序列的方法(Sutskever et al.,2014; Bahdanau et al.,2015)已經證明是非常有效。
然而,儘管深度學習取得了成功,但仍存在重要的批判(Marcus,2001; Shalev-Shwartz et al.,2017; Lake et al.,2017; Lake and Baroni,2018; Marcus,2018a,b; Pearl,2018; Yuille and Liu, 2018)強調了它在複雜的語言和場景理解中所面臨的主要挑戰,對結構化資料的推理,在訓練條件之外的遷移學習,從少量經驗中學習。這些挑戰需要組合泛化,因此避免組合性和顯式結構的方法難以實現,這些挑戰也許並不令人感到驚訝。
當深度學習的聯結主義者(Rumelhart et al.,1987),前輩們面臨著來自結構化的 ,象徵性立場的類似批評時(Fodor and Pylyshyn,1988; Pinker and Prince,1988),有一個建設性的成就(Bobrow and Hinton,1990; Marcus,2001)直接和謹慎地應對挑戰。在類比製造,語言分析,符號操縱和其他形式的關係推理等領域中,開發創新了各種用於表示和推理結構化物件的子符號方法(Smolensky,1990; Hinton,1990; Pollack,1990; Elman,1991; Plate,1995; Eliasmith,2013),以及關於大腦如何工作的更綜合的理論(Marcus,2001)。這些工作還有助於培養更近期的深度學習進展,這些進步使用分散式向量表示來採集文字中豐富的語義內容(Mikolov et al.,2013; Pennington et al.,2014),圖(Narayanan et al.,2016,2017),代數和邏輯表示式(Allamanis et al.,2017; Evans et al.,2018)和程式(Devlin et al.,2017; Chen et al.,2018b)。
我們認為,現代人工智慧的一個關鍵路徑是將組合泛化作為首要任務,我們提倡採用綜合方法來實現這一目標。正如生物學不在先天與後天之間做出選擇- 它共同使用先天和後天,建立大於其各部分總和的整體-我們也拒絕結構和靈活性在某種程度上不一致或不相容的觀念,共同擁有兩者,旨在獲得互補的優勢。 本著最近的許多基於結構化的方法和深度學習的原則混合的精神(Reed and De Freitas,2016; Garnelo et al.,2016; Ritchie et al.,2016; Wu et al.,2017; Denil et al.,2017; Hudson and Manning,2018),我們看到了通過利用完整的AI工具包,並將今天的最佳方法與資料和計算時非常重要的方法相結合來合成新技術的巨大希望。
最近,在深度學習和結構化方法的交叉點上出現了一類模型,其模型側重於對顯式結構化資料進行推理的的方法,特別是圖(Scarselli et al.,2009b; Bronstein et al.,2017; Gilmer et al.,2017; Wang et al.,2018c; Li et al.,2018; Kipf et al.,2018; Gulcehre et al.2018)。這些方法的共同之處在於,在離散實體上執行計算的能力以及它們之間的關係。與傳統的方法區別開來的是,如何學習實體和關係的表示和結構以及相應的計算,從而減輕了需要提前指定它們的負擔。至關重要的是,這些方法帶有強烈的關係歸納偏置,以特定的架構假設的形式,引導這些方法學習實體和關係(Mitchell,1980),我們加入了許多其他方法(Spelke et al.,1992; Spelke and Kinzler,2007; Marcus,2001; Tenenbaum et al.,2011; Lake et al.,2017; Lake and Baroni,2018; Marcus,2018b),建議是類人工智慧的重要組成部分。
在本文的其餘部分,我們通過其關係歸納偏置的視角來研究各種深度學習方法,表明現有方法通常帶有關係假設,這些假設並不總是顯式的或立即可見的。 然後,我們提出了基於實體和關係的推理的一般框架,我們稱之為圖網路,用於統一和擴充套件現有的對圖進行操作的方法,並描述了使用圖網路作為構建塊構建強大架構的關鍵設計原則。
框1:關係推理
我們將結構定義為組成一組已知構建塊的產物。“結構化表示”採集這個組成(即元素的排列),“結構化計算”作為整體對元素及其組成進行的操作。關係推理涉及操縱實體和關係的結構化表示,使用關於如何組成它們的規則。我們使用這些術語來採集認知科學,理論電腦科學和AI的概念,如下所示:
- 實體是具有屬性的元素,例如具有大小和質量的物理物件。
- 關係是實體之間的屬性。兩個物體之間的關係可能包括相同的尺寸,重量和距離。關係也可以具有屬性。超過X倍的關係取一個屬性X,它決定了關係的相對權重閾值是真是假。關係也可能對全域性上下文敏感。對於一個石頭和一根羽毛,這種關係的下降速度要大於上下文是在空氣中還是在真空中。在這裡,我們關注實體之間的配對關係。
- 規則是一個函式(如非二進位制邏輯謂詞),它將實體和關係對映到其他實體和關係,例如像 IS ENTITY X LARGE? 這樣的比例運算,以及 IS ENTITY X HEAVIER THAN ENTITY Y? 。這裡我們考慮採用一個或兩個引數(一元和二元)的規則,並返回一元屬性值。
作為機器學習中關係推理的一個示例,圖模型(Pearl,1988; Koller and Friedman,2009)可以通過在隨機變數之間進行顯式隨機條件獨立來表示複雜的聯合分佈。這些模型非常成功,因為它們採集稀疏結構,這是許多現實世界生成過程的基礎,並且因為它們支援用於學習和推理的高效演算法。例如,隱馬爾可夫模型在給定前一時間的狀態下將潛伏狀態約束為條件獨立於其他狀態,並且考慮到當前時間的潛在狀態,觀察值是條件獨立的,這與以下關係結構完全匹配許多真實世界的因果過程。明確地表達變數之間的稀疏依賴關係提供了各種有效的推理和推理演算法,例如訊息傳遞,它們在圖模型內的各個地方之間應用通用的訊息傳遞過程,從而產生可組合的和部分可並行的推理過程,應用於不同尺寸和形狀的圖形模型。
2 關係歸納偏差
機器學習和AI中有許多具有關係推理能力的方法(框1)使用關係歸納偏差。雖然不是一個精確的、正式的定義,但我們使用這個術語來指代歸納偏置(框2),它對學習過程中對實體之間的關係和相互作用施加約束。
框2:歸納偏置
學習是通過觀察和與訊息互動來理解有用知識的過程。它涉及搜尋一個解決方案的空間,以期提供更好的資料解釋或獲得更高的回報。但在許多情況下,有多種解決方案同樣出色(Goodman,1955)。歸納偏置允許學習演算法將一種解決方案(或解釋)優先於另一種解決方案(或獨立於觀察到的資料)(Mitchell,1980)。在貝葉斯模型中,歸納偏置通常通過先驗分佈的選擇和引數化來表達(Griffi ths et al.,2010)。在其他情況下,歸納偏置可能是一個正則化項(McClelland,1994),用以避免過擬合,或者它可能在演算法本身的架構中編碼。歸納偏置通常會以犧牲靈活性為代價,提高樣本的複雜性,並且可以根據偏差-方差權衡來理解(Geman et al.,1992)。理想情況下,歸納偏置既可以改善對解決方案的搜尋,又不會明顯降低效能,還可以幫助找到以理想方式推廣的解決方案;然而,不匹配的歸納偏置也可能通過引入過於強大的約束而導致次優效能。
歸納偏差可以表達關於資料生成過程或解決方案空間的假設。例如,當將一維函式擬合到資料時,線性最小二乘遵循約束函式是線性模型,並且在二次懲罰下近似誤差應該是最小的。這反映了一種假設,即資料生成過程可以簡單地解釋為,因為線性過程被加性高斯噪聲破壞。類似地,L2正則化優先考慮其引數具有較小值的解決方案,並且可以針對其他不適合的問題引入獨特的解決方案和全域性結構。這可以解釋為關於學習過程的假設:當解決方案之間的模糊程度較小時,搜尋到好的解決方案會更容易。注意,這些假設不需要是顯式的-它們反映了模型或演算法如何與訊息相連線。
創新的新機器學習架構近年來迅速發展,(本文的主題可能並不令人驚訝)實踐者經常遵循組成基本構建模組的設計模式,以形成更復雜,更深的計算層次結構和圖形。諸如“完全連線”層的構建塊被堆疊成“多層感知器”(MLP),“卷積層”被堆疊到“卷積神經網路”(CNN),並且用於影象處理網路的標準配方通常是一些由MLP組成的各種CNN。這種層的組合提供了特定型別的關係歸納偏置- 分層處理-其中分階段進行計算,通常導致輸入訊號中的資訊之間的長距離互動。正如我們在下面探討的那樣,構建塊本身也帶有各種關係歸納偏置(表1)。雖然超出了本文的範圍,但深度學習中也使用了各種非關係歸納偏置:例如,啟用非線性,權重衰減,丟失(Srivastava et al.,2014),批量和層歸一化(Io ff e and Szegedy,2015; Ba et al.,2016),資料增強,訓練課程和優化演算法都對學習的軌跡和結果施加了限制。
| 元件 | 實體 | 關係 | 關係性推斷偏好(RIBs) | 不變性 |
|---|---|---|---|---|
| 全連線 | 單元(Units) | 多對多 | 弱 | - |
| 卷積 | 網格元素 | 區域性 | 區域性性 | 空間平移 |
| 迴圈 | 時間步(Timesteps) | 時序 | 序列性 | 時間平移 |
| 圖網路 | 節點 | 邊 | 隨意的 | 節點、邊的排列 |
表1:標準深度學習元件中的各種關係歸納偏見。另參見第2節。
為了探索在各種深度學習方法中表達的關係歸納偏置,我們必須確定幾個關鍵要素,類似於框1中的那些:實體是什麼,關係是什麼,構成實體和關係的規則是什麼,以及計算它們的意義?在深度學習中,實體和關係通常表示為分散式表示,而規則表示為神經網路函式逼近器;然而,實體,關係和規則的精確形式因架構而異。為了理解架構之間的這些差異,我們可以通過探測進一步詢問每個架構如何支援關係推理:
- 規則函式的引數(例如,哪些實體和關係作為輸入提供)。
- 規則函式如何在計算圖中重複使用或共享(例如,跨越不同的實體和關係,跨越不同的時間或處理步驟等)。
- 架構如何定義表示之間的互動與隔離(例如,通過應用規則來得出關於相關實體的結論,而不是單獨處理它們)。
2.1 標準深度學習構建塊中的關係歸納偏置
2.1.1 全連線層
也許最常見的構建塊是全連線層(Rosenblatt,1961)。通常作為向量輸入的非線性向量值函式實現,輸出向量的每個元素或“單位”是權重向量之間的點積,後跟增加的偏置項,最終是非線性的點積作為修正線性單元(ReLU)。因此,實體是網路中的單元,關係是全部到全部的(層 中的所有單元都連線到層 中的所有單元),並且規則由權重和偏置指定。該規則的論證是完整的輸入訊號,沒有重用,並且沒有資訊隔離(圖1a)。 因此,完全連線層中的隱式關係歸納偏置非常弱:所有輸入單元可以相互作用以確定任何輸出單元的值,獨立地跨輸出(表1)。
2.1.2 卷積層
另一個常見的構建塊是卷積層(Fukushima,1980; LeCun et al.,1989)。它通過將輸入向量或張量與相同等級的卷積核進行卷積,新增偏置項並應用逐點非線性來實現。這裡的實體仍然是單獨的單元(或網格元素,例如畫素),但是這些關係更稀疏。全連線層和卷積層之間的差異強加了一些重要的關係歸納偏差:區域性性和平移不變性(圖1b)。區域性性反映出關係規則的論證是在輸入訊號的座標空間中彼此靠近的實體,與遠端實體隔離。平移不變性反映了輸入中跨地區重用相同的規則。這些偏差對於處理自然影象資料非常有效,因為在區域性鄰域記憶體在較高的協方差,其隨著距離增加而減小,並且因為統計資料在影象上大部分是靜止的(表1)。

圖1:在通用的深度學習構建塊中重用和共享。(a) 全連線層,全部的權重都是獨立的,不存在共享。 (b) 卷積層,區域性核函式在輸入上重用了多次。共享的權重用相同顏色的箭頭指明。(c) 迴圈層,同樣的函式在不同處理階段被重用。
2.1.3 迴圈層
第三個常見構建塊是迴圈層(Elman,1990),它是通過一系列步驟實現的。 在這裡,我們可以將每個處理步驟中的輸入和隱藏狀態視為實體,並將前一隱藏狀態和當前輸入的隱藏狀態的馬爾可夫依賴性視為關係。組合實體的規則將步驟的輸入和隱藏狀態作為引數來更新隱藏狀態。該規則在每個步驟中被重複使用(圖1c),這反映了時間不變性的關係歸納偏置(類似於CNN在空間中的平移不變性)。例如,一些事件的物理順序的結果不應該取決於一天的時間。RNNs也通過它們的馬爾可夫結構對序列中的位置產生偏差(表1)。
2.2 集合和圖的計算
雖然標準深度學習工具包包含具有各種形式的關係歸納偏置的方法,但是沒有“預設”深度學習元件在任意關係結構上執行。我們需要具有實體和關係的明確表示的模型,以及用於計算其互動的規則的學習演算法,以及將它們置於資料中的方法。重要的是,世界上的實體(如物件和代理人)沒有自然秩序; 相反,排序可以通過他們關係的屬性來定義。例如,一組物體的大小之間的關係可以用來對它們進行排序,它們的質量,年齡,毒性和價格也可以。除了面對關係之外,順序不變性是理想情況下應該通過關係推理的深度學習元件反映的屬性。
集合是用於由其順序是不確定的或不相關的實體描述的系統的自然表示;特別的,他們的關係歸納偏差不是來自某事物的存在,而是來自缺乏。為了說明,考慮預測由n個行星組成的太陽系質心的任務,其屬性(例如,質量,位置,速度等)由 表示。對於這樣的計算,我們認為行星的順序無關緊要,因為狀態可以僅用匯總的平均數量來描述。然而,如果我們使用一個MLP來完成此任務,那麼學習某個特定輸入 的預測就不一定會轉化為在不同的排序下對相同輸入進行預測 。既然有 種可能的排序,在最壞的情況下,MLP可以將每個排序視為不同,因此需要指數數量的輸入/輸出訓練示例來學習近似函式。處理這種組合爆炸的一種自然方法是隻允許預測依賴於輸入屬性的對稱函式。這可能意味著計算共享的每個物件特徵 ,然後以對稱的方式進行聚合(例如,通過取其平均值)。這種方法是Deep Sets模型的本質(Zaheer et al.,2017),我們將在4.2.3節進一步探討。

圖2:不同的圖表示方法。(a)一個分子,每一個節點代表一個原子,邊代表化學鍵(e.g. Duvenaud et al., 2015)。(b) A mass-spring system, in which the rope is defined by a sequence of masses which are represented as nodes in the graph (e.g. Battaglia et al., 2016; Chang et al., 2017). © A n-body system, in which the bodies are nodes and the underlying graph is fully connected (e.g. Battaglia et al., 2016; Chang et al., 2017). (d) A rigid body system, in which the balls and walls are nodes, and the underlying graph defines interactions between the balls and between the balls and the walls (e.g. Battaglia et al., 2016; Chang et al., 2017). (e) A sentence, in which the words correspond to leaves in a tree, and the other nodes and edges could be provided by a parser (e.g. Socher et al., 2013). Alternately, a fully connected graph could be used (e.g. Vaswani et al., 2017). (f) An image, which can be decomposed into image patches corresponding to nodes in a fully connected graph (e.g. Santoro et al., 2017; Wang et al., 2018c).
當然,在許多問題中,置換不變性不是唯一重要的基本結構形式。例如,一個集合中的每個物件都可能受到與集合中的其他物件的成對互動而帶來的影響。 在我們的行星場景中,現在考慮在一個時間間隔 之後預測每個行星位置的任務。在這種情況下,使用聚合的平均資訊是不夠的,因為每個行星的運動取決於其他行星對其施加的力。相反,我們可以將每個物件的狀態計算為 ,其中 可以計算第 個行星在第 個行星上引起的力, 可以計算由力和動力學產生的第 個行星的未來狀態。我們在任何地方使用相同的 的事實也是系統的全域性置換不變性的結果; 然而,它也支援不同的關係結構,因為 現在需要兩個引數而不是一個引數。
上述太陽系例項說明了兩種關係結構:一種是不存在的關係,一種包含所有配對關係。許多現實世界的系統(如圖2所示)在這兩個極端之間的某處具有一個關係結構,然而,一些實體擁有一個關係而另一些實體沒有關係。在我們的太陽系例子中,如果系統由行星和它們的衛星組成,那麼人們可能會試圖通過忽略不同行星的衛星之間的相互作用來近似它。在實際中,這意味著僅計算一些物件之間的互動作用,即 ,其中 是節點 的鄰域。這對應於一個圖,因為第 個物件僅與其鄰域描述的其他物件的子集互動。注意,更新後的狀態仍然不依賴於我們描述鄰域的順序。
通常,圖是支援任意(成對)關係結構的表示,並且圖上的計算可以是強大的關係歸納偏差,超出卷積層和迴圈層可以提供的強關係式感應偏差。
3 圖網路
在圖形神經網路的保護下,神經網路在圖形上執行並相應地構建其計算,已經被廣泛開發和探索了十多年(Gori et al.,2005; Scarselli et al.,2005,2009a; Li et al.,2016),但近年來在範圍和流行性方面發展迅速。我們在下一小節(3.1)中對這些方法的文獻進行了調查。然後在剩下的部分中,我們展示了我們的圖網路框架,該框架概括並擴充套件了該領域的工作。
3.1 背景
圖神經網路家族中的模型(Gori et al.,2005; Scarselli et al.,2005,2009a; Li et al.,2016)已經在各種問題領域中進行了探索,涵蓋監督,半監督,無監督和強化學習等環境。他們對於被認為具有豐富關係結構的任務非常有效,例如視覺場景理解任務(Raposo et al.,2017; Santoro et al.,2017)和少數學習(Garcia and Bruna,2018)。它們也被用來學習物理系統的動力學(Battaglia et al.,2016; Chang et al.,2017; Watters et al.,2017; van Steenkiste et al.,2018; Sanchez-Gonzalez et al.,2018) )和多智慧體系統(Sukhbaatar et al.,2016; Hoshen,2017; Kipf et al.,2018),推理知識圖(Bordes et al.,2013; On ~oro-Rubio et al.,2017; Hamaguchi et al.,2017)預測分子的化學性質(Duvenaud et al.,2015; Gilmer et al.,2017),以預測道路上的交通(Cui et al.,2018),對視訊進行分類和分類(Wang et al.,2018c)和3D網格和點雲(Wang et al.,2018d),對影象中的區域進行分類(Chen et al.,2018a),以執行半監督文字分類(Kipf and Welling,2017)和機器翻譯(Vaswani et al.,2017; Shaw et al.,2018; Gulcehre et al.,2018)。它們已被用於無模型(Wang et al.,2018b)和基於模型(Hamrick et al.,2017; Pascanu et al.,2017; Sanchez-Gonzalez et al.,2018)的連續控制,用於模型 - 免費強化學習(Hamrick et al.,2018; Zambaldi et al.,2018),以及更經典的規劃方法(Toyer et al.,2017)。
許多傳統的電腦科學問題,包括關於離散實體和結構的推理,也已經用圖神經網路進行了探索,例如組合優化(Bello et al.,2016; Nowak et al.,2017; Dai et al.,2017) ,布林滿意度(Selsam et al.,2018),程式表示和驗證(Allamanis et al.,2018; Li et al.,2016),細胞自動機和圖靈機的建模(Johnson,2017),並在圖模型中進行推理(Yoon et al.,2018)。最近的工作還集中在構建圖的生成模型(Li et al.,2018; De Cao and Kipf,2018; You et al.,2018; Bojchevski et al.,2018),以及圖形嵌入的無監督學習(Perozzi et al.,2014; Tang et al.,2015; Grover and Leskovec,2016;Garc’ıa-Dura’n and Niepert,2017)。
上面引用的作品絕不是詳盡的列表,而是提供了圖神經網路已經被證明有用的域的廣度的代表性橫截面。我們將感興趣的讀者指向一些現有的評論,這些評論更深入地研究了圖神經網路的工作主體。特別是,Scarselli等人(2009a)提供了早期圖神經網路方法的權威概述。布朗斯坦等人(2017)提供了非歐幾里德資料深度學習的優秀調查,並探索了圖神經網路,圖卷積網路和相關的頻譜方法。最近,吉爾默等人(2017)引入了訊息傳遞神經網路(MPNN),其統一了各種圖神經網路和圖卷積網路的方法(Monti et al.,2017; Bruna et al.,2014; Hena ff et al.,2015; Defferrard et al.,2016; Niepert et al.,2016; Kipf and Welling,2017; Bronstein et al.,2017),類比於圖模型中的訊息傳遞。同樣,Wang等人(2018c)引入了非區域性神經網路(NLNN),它通過類比方法統一了各種“自我關注”式方法(Vaswani et al.,2017; Hoshen,2017; Velickovi’c et al.,2018)。從計算機視覺和圖模型中採集訊號中的長距離依賴性。
3.2 圖網路(GN)塊
我們現在展示我們的圖網路(GN)框架,它為圖形結構表示定義了一類關係推理的函式。我們的GN框架概括和擴充套件了各種圖形神經網路,MPNN和NLNN方法(Scarselli et al.,2009a; Gilmer et al.,2017; Wang et al.,2018c),並支援從簡單的構建塊構建複雜的體系結構。注意,我們避免在“圖網路”標籤中使用術語“神經”來反映它們可以用除神經網路之外的函式來實現,儘管這裡我們關注的是神經網路實現。
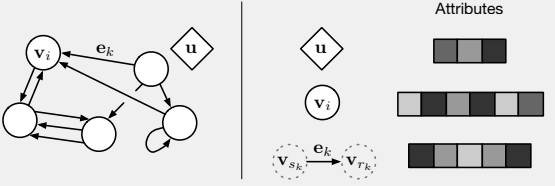
GN框架中的主要計算單元是GN塊,即“圖形到圖形”的模組,它將圖形作為輸入,對結構執行計算,並返回圖形作為輸出。如方框3所述,實體由圖的節點,邊緣的關係和全域性屬性的系統級屬性表示。GN框架的塊組織強調可定製性併合成表達所需關係歸納偏差的新架構。關鍵設計原則是:靈活的表示(見4.1節); 可配置的塊內結構(見4.2節); 和可組合的多塊體系結構(參見第4.3節)。
框3:我們對“圖 ”的定義
這裡我們用“圖”來代表一個含有全域性屬性的、有向的、有屬性的多圖。在我們的術語中,單個節點表示為 ,單個邊表示為