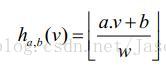上一節，我們分析了LSH演算法的通用框架，主要是建立索引結構和查詢近似最近鄰。這一小節，我們從p穩定分佈LSH（p-Stable LSH）入手，逐漸深入學習LSH的精髓，進而靈活應用到解決大規模資料的檢索問題上。

對應海明距離的LSH稱為位取樣演算法（bit sampling），該演算法是比較得到的雜湊值的海明距離，但是一般距離都是用歐式距離進行度量的，將歐式距離對映到海明空間再比較其的海明距離比較麻煩。於是，研究者提出了基於p-穩定分佈的位置敏感雜湊演算法，可以直接處理歐式距離，並解決(R,c)-近鄰問題。

1、p-Stable分佈

定義：對於一個實數集R上的分佈D，如果存在P>=0，對任何n個實數v₁

對任何p∈(0,2]存在穩定分佈：

p=1是柯西分佈，概率密度函式為c(x)=1/[π(1+x²)]；

p=2時是高斯分佈，概率密度函式為g(x)=1/(2π)^1/2*e^{-x^2/2}。

利用p-stable分佈可以有效的近似高維特徵向量，並在保證度量距離的同時，對高維特徵向量進行降維，其關鍵思想是，產生一個d維的隨機向量a，隨機向量a中的每一維隨機的、獨立的從p-stable分佈中產生。對於一個d維的特徵向量v，如定義，隨機變數a·v具有和(Σ

2、p-Stable分佈LSH中的雜湊函式

p-Stable分佈的LSH利用p-Stable的思想，使用它對每一個特徵向量v賦予一個雜湊值。該雜湊函式是區域性敏感的，因此如果v1和v2距離很近，它們的雜湊值將相同，並被雜湊到同一個桶中的概率會很大。

根據p-Stable分佈，兩個向量v1和v2的對映距離a·v₁-a·v₂和||v₁-v₂||_pX 的分佈是一樣的。

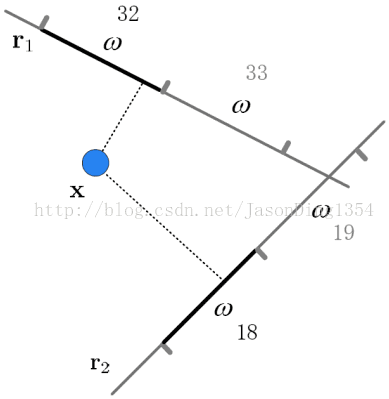
a·v將特徵向量v對映到實數集R，如果將實軸以寬度w等分，並對每一段進行標號，則a·v落到那個區間，就將此區間標號作為雜湊值賦給它，這種方法構造的雜湊函式對於兩個向量之間的距離具有區域性保護作用。

雜湊函式格式定義如下：

h_a,b(v):R^d->N，對映一個d維特徵向量v到一個整數集。雜湊函式中又兩個隨機變數a和b，其中a為一個d維向量，每一維是一個獨立選自滿足p-Stable的隨機變數，b為[0,w]範圍內的隨機數，對於一個固定的a，b，則雜湊函式h_a,b(v)為

圖1 p-Stable LSH在二維空間的示例

3、特徵向量碰撞概率

隨機選取一個雜湊函式h_a,b(v)，則特徵向量v1和v2落在同一桶中的概率該如何計算呢？

首先定義c=||v₁-v₂||_p，f_p(t)為p-Stable分佈的概率密度函式的絕對值，那麼特徵向量v1和v2對映到一個隨機向量a上的距離是|a·v₁-a·v₂|<w，即|(v₁-v₂)·a|<w，根據p-Stable分佈的特性,||v₁-v₂||_pX=|cX|<w，其中隨機變數X滿足p-Stable分佈。

可得其碰撞概率p(c):

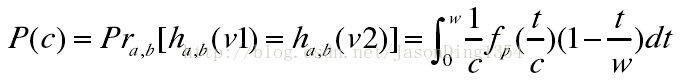
根據該式，可以得出兩個特徵向量的衝突碰撞概率隨著距離c的增加而減小。

4、p-Stable分佈LSH的相似性搜尋演算法

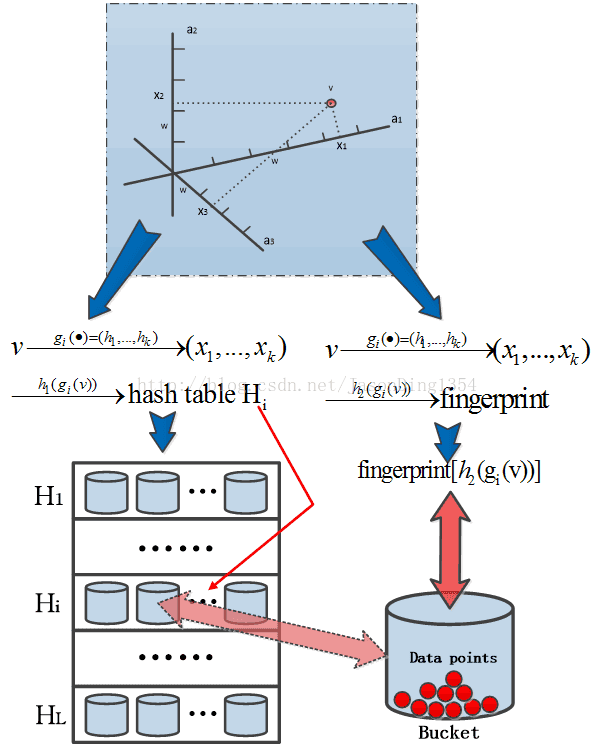
經過雜湊函式雜湊之後，g(v)=(h1(v),...,hk(v))，但將(h1(v),...,hk(v))直接存入雜湊表，即佔用記憶體，又不便於查詢，為解決此問題，現定義另外兩個雜湊函式：

由於每一個雜湊桶（Hash Buckets）g_i被對映成Z_k，函數h1是普通雜湊策略的雜湊函式，函式h2用來確定鏈表中的雜湊桶。

（1）要在一個連結串列中儲存一個雜湊桶gi(v)=(x1,...,xk)時，實際上存的僅僅是h2(x1,...,xk)構造的指紋,而不是儲存向量(x1,...,xk)，因此一個雜湊桶gi(v)=(x1,...,xk)在連結串列中的相關資訊僅有標識(identifier)指紋h2(x1,...,xk)和桶中的原始資料點。

（2）利用雜湊函式h2，而不是儲存gi(v)=(x1,...,xk)的值有兩個原因：首先，用h2(x1,...,xk)構造的指紋可以大大減少雜湊桶的儲存空間；其次，利用指紋值可以更快的檢索雜湊表中雜湊桶。通過選取一個足夠大的值以很大的概率來保證任意在一個連結串列的兩個不同的雜湊桶有不同的h2指紋值。

圖2 桶雜湊策略示意圖

5、不足與缺陷

LSH方法存在兩方面的不足：首先是典型的基於概率模型生成索引編碼的結果並不穩定。雖然編碼位數增加，但是查詢準確率的提高確十分緩慢；其次是需要大量的儲存空間，不適合於大規模資料的索引。E2LSH方法的目標是保證查詢結果的準確率和查全率，並不關注索引結構需要的儲存空間的大小。E2LSH使用多個索引空間以及多次雜湊表查詢，生成的索引檔案的大小是原始資料大小的數十倍甚至數百倍。

參考資料：

1、王旭樂.基於內容的影象檢索系統中高維索引技術的研究[D].華中科技大學.2008

2、M.Datar,N.Immorlica,P.Indyk,and V.Mirrokni,“Locality-SensitiveHashing Scheme Based on p-Stable Distributions,”Proc.Symp. ComputationalGeometry, 2004.

3、A.Andoni,“Nearest Neighbor Search:The Old, theNew, and the Impossible”PhD dissertation,MIT,2009.

4、A.Andoni,P.Indyk.E2lsh:Exact Euclidean locality-sensitive hashing.http://web.mit.edu/andoni/www/LSH/.2004.