你會學到什麼？

樹的遞迴遍歷演算法很容易理解，程式碼也很精簡，但是如果想要從本質上理解二叉樹常用的三種遍歷方法，還得要思考樹的非遞迴遍歷演算法。

讀完後的收穫：

• 您將學到二叉樹的中序遍歷的非遞迴版本
• 明白棧這種資料結構該怎麼使用

討論的問題是什麼？

主要討論二叉樹的非遞迴版中序遍歷該如何實現，包括藉助什麼樣的資料結構，迭代的思路等。

這個問題相關的概念和理論

遍歷

Traversal 指沿著某條搜尋路線，依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴於具體的應用問題。

二叉樹組成

二叉樹由根結點及左、右子樹這三個基本部分組成。

中序遍歷

Inorder Traversal 訪問根結點的操作發生在遍歷其左、右子樹之中間。

非遞迴版中序遍歷演算法

這裡我們以二叉樹為例，討論二叉樹的中序遍歷的非遞迴版實現。

我們先看下二叉樹的節點TreeNode的資料結構定義。

節點的資料域的型別定義為泛型 T，含有左、右子樹，及一個帶有資料域的建構函式。

   public class TreeNode<T>
    {
        public T val { get; set; }

        public TreeNode<T> left { get; set; }
        public
 
 TreeNode<T> right { get; set; }

        public TreeNode(T data)
        {
            val = data;
        }
    }

程式碼思考

中序遍歷，首先遍歷左子樹，根節點，最後右子樹，這裡的順序性，我們藉助棧 First In Last Out 的資料結構，演算法的思路：

1. 引數root (TreeNode) 如果是空引用，直接返回；

2. 初始化棧，並把root節點Push到棧 s

3. 遍歷（條件為棧s內有元素）

4. 找最左的節點同時，將左子樹的左節點依次Push到棧s。這裡有兩種情況，第一種是一上來就滿足while條件，即滿足 while(context!=null) ，當退出迴圈時，context.left必等於null，也就是s棧頂必為null元素；第二種，不滿足while條件（可能發生在某次遍歷），這個棧內的null元素就是演算法對每個葉子節點虛擬出的另一個子右節點null

5. s.pop，此處出棧元素必為null

6. s.Count為0，則直接返回。這種情況可能發生在根節點只有左子樹，沒有右子樹的情況，見下方的快照圖

7. 訪問棧頂元素TopNode（相對於棧頂元素的後面一個元素NextNode而言，此節點為其左節點）

8. Pop掉這個節點TopNode

9. 此時棧頂元素為NextNode，其右節點Push到s，到此完成一次遍歷

10. 重複3~9，直到不滿足3的遍歷條件時退出。也就說在一次遍歷過程中，可能發生一次或多次Push，Pop操作除了最後一次遍歷外，其餘都是兩次Pop。

演算法技巧

演算法對每個葉子節點虛擬出另一個子右節點，具體對應步驟9。

實現程式碼

public IList<T> InorderTraversal<T>(TreeNode<T> root)
        {
            IList<T> rtn = new List<T>();
            //1
            if (root == null) 
                  return rtn;  
            //2
            var s = new Stack<TreeNode<T>>();
              s.Push(root);         
            while (s.Count > 0) //3
            {
               //4
                var context = s.Peek();
                while (context != null) 
                {
                    s.Push(context.left);
                    context = context.left;
                }               
                s.Pop();//5
               //6
                if (s.Count == 0)
                    return rtn;              
                rtn.Add(s.Peek().val); //7          
                TreeNode<T> curNode = s.Pop(); //8             
                s.Push(curNode.right);//9
            }
            return rtn;
      }

快照

如下圖所示，中序遍歷已經訪問完了節點5，此時棧s內的元素為null和3，

下一個要訪問的元素是節點3，是如何訪問的呢？重複步驟3~9。此時的棧頂為null，不滿足步驟4的條件，執行步驟5出棧null元素，不滿足步驟6的條件，執行步驟7訪問此時的棧頂即節點3，執行步驟8即出棧元素3，執行步驟9將右子節點（虛擬出的null如上圖所示）入棧s，結果如下圖所示，

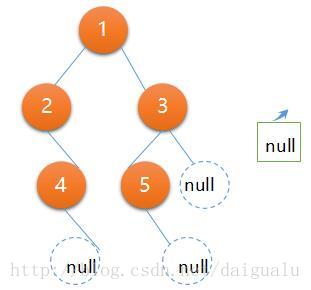
到此所有的節點都訪問一遍，訪問的順序： 2->4->1->5->3。但是程式還會再遍歷一次，因為此時的棧不為空（含有null）。

執行步驟10即執行下一次遍歷，此時棧s含有一個元素null，執行步驟4拿到棧頂元素並且不滿足while條件，執行步驟5，結果棧內元素變空，滿足了步驟6的條件，

 if (s.Count == 0)
  return rtn;       

直接返回，如下圖所示，

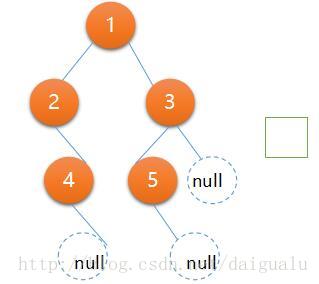
評價演算法

非遞迴版中序遍歷演算法的時間複雜度為 O(n)，空間複雜度為棧所佔的記憶體空間為 O(n)。

總結

討論了二叉樹的非遞迴版中序遍歷演算法，演算法藉助棧，巧妙地對每個葉子節點虛擬出一個子右節點，按照左子樹，根節點，右子樹的遍歷次序訪問整棵樹，時間和空間複雜度都為 O(n)。

如果，想了解 圖解二叉樹非遞迴版的前序遍歷演算法，請關注下面公眾號。

歡迎關注《演算法思考與應用》公眾號

如果，想了解 圖解二叉樹非遞迴版的前序遍歷演算法，請關注下面公眾號。