筆記二:計數排序、選擇排序、氣泡排序、插入排序
計數排序
1、 名次 :所謂名次,通俗理解即為該元素在序列中排行老幾的意思。
2.、如何求名次:依次對每一個元素進行比較,若排在自己(該元素)前面的元素比自己大,則前面的元素在排行計數上加1,反之則自己加1。
3、利用附加陣列的計數排序:根據自身名次重新整理一份排序序列儲存在附加陣列中,然後將附加陣列值拷貝到原序列中。
1)程式碼:
template<typename T> void SortClass<T>::rank(T a[], int n, int r[])
{
//給陣列a[0: n-1]的n個元素排名次
//結果在r[0: n-1]中返回
for 2)執行:
3)時間複雜度分析:在求名次rank()操作中,針對第i個元素,比較的次數為i次,因此總的比較次數為:1+2+3+…+(n-1)=(n-1)n/2次。在rearrange()中有2次for迴圈進行賦值操作,總的移動次數是2n。兩者相加,得出附加陣列的計數排序時間複雜度為:(n-1)n/2+2n =O(n2)(注:2為n的上標)
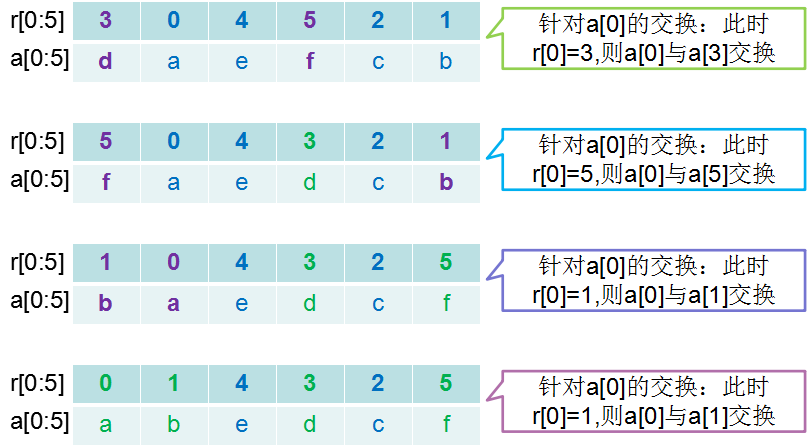
4、原地排序:所謂原地排序就是指在對序列元素進行名次計算之後,根據名次調整原序列的順序,不借助附加陣列。
1)思路:假設第一個元素a[0]的名次r[0]=3,那麼,a[0]的值應該交換到下標為3的位置,即a[0]與a[3]交換。由於元素位置交換了,那麼相應的,元素對應名次也要交換。停止交換的前提是a[0]元素對應的r[0]正好為0,則此時a[0]才是正確的元素。對其他位置元素,同理。
2 ) 程式碼:
template<typename T> void SortClass<T>::selfrearrange(T a[], int n)
{
int *r = new int[n]; //儲存陣列元素名次
rank(a, n, r);
for (int i = 0; i < n; i++)
while (i != r[i]) //當i == r[i]時,表明名次對應的下標儲存元素正確
{
int tmp = r[i];
swap(a[i], a[tmp]); //元素交換
swap(r[i], r[tmp]); //排名交換
}
delete[] r;
}//selfrearrange3)執行:
4)時間複雜度分析:名次比較次數:1+2+3+…+(n-1)=(n-1)n/2次。交換次數:當序列有序時,交換0次,當序列無序時,由於每次交換,至少使一個元素交換到正確位置,那麼對任意一個元素而言,最多的交換次序是(n-1)次,在這(n-1)次交換中,其他元素也被交換正確,故最多的交換次數為(n-1)次。原地重排最壞的時間複雜度為:(n-1)n/2+(n-1)=O(n2)。
選擇排序
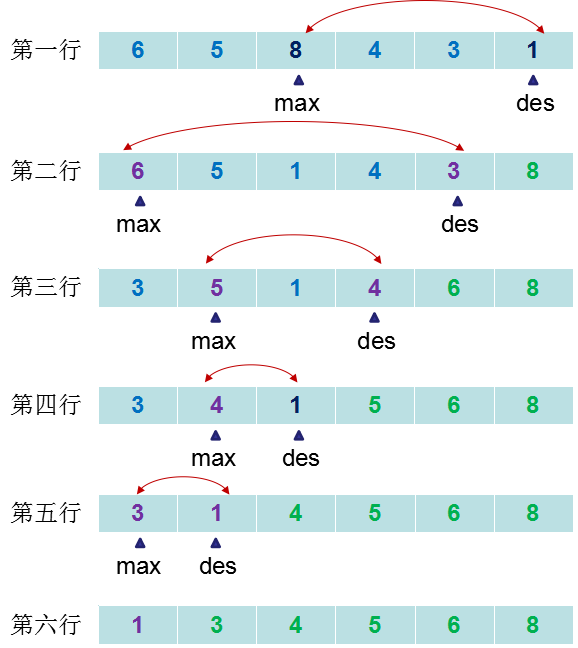
1、定義:第一次遍歷序列,找出最大元素,將該元素排到末尾去;第二次遍歷序列,找出次最大元素,將該元素排到末尾前一位置去;同理,繼續下去,直到最後一個元素為止。
2、思路:
3、基礎選擇排序:按照2中思路進行設計
1)程式碼:
template<typename T> void SortClass<T>::selectionSort(T a[], int n)
{
for (int i = n - 1; i > 0; i--) //移動的目標位置
{
int indexOfMax = 0;
for (int j = 0; j < i; j++) //找最大元素
if (a[indexOfMax] < a[j])
indexOfMax = j;
swap(a[i], a[indexOfMax]); //將最大值移到目標位置
}
}//selectionSort2)執行:
3)時間複雜度分析:在進行查詢最大元素值過程中,比較次數為(n-1)n/2。一次swap()操作,實際包含3步tmp=a;a=b;b=a;,故移動次數為3(n-1)。基礎選擇排序的時間複雜度為(n-1)n/2+3(n-1)=O(n2)。
4、及時終止選擇排序:在查詢最大元素時,同時檢查陣列是否有序,減少不必要的迭代。
1)程式碼:
template<typename T> void SortClass<T>::selectionSortByOrder(T a[], int n)
{
bool sorted = false;
for (int i = n - 1; i > 0 && !sorted; i--) //未排好序的情況下進行選擇排序
{
int indexOfMax = 0;
sorted = true;
for (int j = 0; j < i; j++)
if (a[indexOfMax] < a[j])
{
indexOfMax = j;
}
else
{
sorted = false;
}
swap(a[i], a[indexOfMax]);
}
}//selectionSortByOrder2)執行:
氣泡排序
1、定義:簡單來講,相鄰元素之間的比較,若前者較大,則交換。一輪比較即為一次冒泡過程。
2、基礎氣泡排序:
1)程式碼:
template<typename T> void SortClass<T>::bubbleSort(T a[], int n)
{
for (int i = 0; i < n; i++)
for (int j = 0; j < n - 1; j++)
if (a[j] > a[j + 1])
swap(a[j], a[j + 1]);
}//bubbleSort2)執行:
3、及時終止的氣泡排序:
1)程式碼:
template<typename T> void SortClass<T>::bubbleSortByOrder(T a[], int n)
{
bool sorted = true;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n - 1; j++)
if (a[j] > a[j + 1])
{
swap(a[j], a[j + 1]);
sorted = false; //只要交換順序,表明排序未結束
}
if (sorted)
break;
}
}//bubbleSortByOrder2)執行:
插入排序
1、定義: 把序列第一個元素看做一個有序陣列,將第2個元素按順序插入到這個陣列中,則這兩個陣列組成一個新的有序陣列。將第3個元素插入到上述有序陣列中,那麼這3個有序陣列又組成新的有序陣列。如此,依次將後續元素插入到前面已排好的序列中,直至最後一個元素為止。
2、將要插入元素與已知排序陣列進行比較,從後往前逐一比較,若該元素較小,則將有序陣列中元素後移一位,直到騰出可以插入的空位即可。
3、插入排序:
1)程式碼:
template<typename T> void SortClass<T>::insertSort(T a[], int n)
{
for (int i = 1; i < n; i++)
{
int j;
int tmp = a[i];
for (j = i - 1; j >= 0 && a[j] > tmp; j--) //將大於a[i]的元素依次後移
{
a[j + 1] = a[j];
}
a[j + 1] = tmp; //將a[i]元素按順序插入到a[0:i-1]中
}
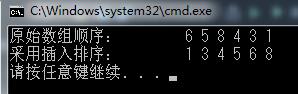
}//insertSort2)執行:
附全程式碼:
#include<iostream>
using namespace std;
template <typename T> class SortClass
{
public:
void rank(T a[], int n, int r[]); //名次計算
void rearrange(T a[], int n); //利用附加陣列計數排序
void selfrearrange(T a[], int n); //原地排序
void selectionSort(T a[], int n); //選擇排序
void selectionSortByOrder(T a[], int n); //及時終止的選擇排序
void bubbleSort(T a[], int n); //氣泡排序
void bubbleSortByOrder(T a[], int n); //及時終止的氣泡排序
void insertSort(T a[], int n); //插入排序
};
template<typename T> void SortClass<T>::rank(T a[], int n, int r[])
{
//給陣列a[0: n-1]的n個元素排名次
//結果在r[0: n-1]中返回
for (int i = 0; i < n; i++)
r[i] = 0;
//比較所有元素,每次比較中較大元素計數器加1
for (int i = 0; i < n; i++)
for (int j = 0; j < i; j++)
if (a[j] <= a[i])
{
++r[i];
}
else
{
++r[j];
}
}//rank
template<typename T> void SortClass<T>::rearrange(T a[], int n)
{
T *u = new T[n]; //臨時陣列,儲存排序元素
int *r = new int[n]; //儲存陣列元素名次
rank(a, n, r);
for (int i = 0; i < n; i++)
u[r[i]] = a[i];
for (int i = 0; i < n; i++)
a[i] = u[i];
delete [] u;
delete[] r;
}//rearrange
template<typename T> void SortClass<T>::selfrearrange(T a[], int n)
{
int *r = new int[n]; //儲存陣列元素名次
rank(a, n, r);
for (int i = 0; i < n; i++)
while (i != r[i]) //當i == r[i]時,表明名次對應的下標儲存元素正確
{
int tmp = r[i];
swap(a[i], a[tmp]); //元素交換
swap(r[i], r[tmp]); //排名交換
}
delete[] r;
}//selfrearrange
template<typename T> void SortClass<T>::selectionSort(T a[], int n)
{
for (int i = n - 1; i > 0; i--) //移動的目標位置
{
int indexOfMax = 0;
for (int j = 0; j < i; j++) //找最大元素
if (a[indexOfMax] < a[j])
indexOfMax = j;
swap(a[i], a[indexOfMax]); //將最大值移到目標位置
}
}//selectionSort
template<typename T> void SortClass<T>::selectionSortByOrder(T a[], int n)
{
bool sorted = false;
for (int i = n - 1; i > 0 && !sorted; i--) //未排好序的情況下進行選擇排序
{
int indexOfMax = 0;
sorted = true;
for (int j = 0; j < i; j++)
if (a[indexOfMax] < a[j])
{
indexOfMax = j;
}
else
{
sorted = false;
}
swap(a[i], a[indexOfMax]);
}
}//selectionSortByOrder
template<typename T> void SortClass<T>::bubbleSort(T a[], int n)
{
for (int i = 0; i < n; i++)
for (int j = 0; j < n - 1; j++)
if (a[j] > a[j + 1])
swap(a[j], a[j + 1]);
}//bubbleSort
template<typename T> void SortClass<T>::bubbleSortByOrder(T a[], int n)
{
bool sorted = true;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n - 1; j++)
if (a[j] > a[j + 1])
{
swap(a[j], a[j + 1]);
sorted = false; //只要交換順序,表明排序未結束
}
if (sorted)
break;
}
}//bubbleSortByOrder
template<typename T> void SortClass<T>::insertSort(T a[], int n)
{
for (int i = 1; i < n; i++)
{
int j;
int tmp = a[i];
for (j = i - 1; j >= 0 && a[j] > tmp; j--) //將大於a[i]的元素依次後移
{
a[j + 1] = a[j];
}
a[j + 1] = tmp; //將a[i]元素按順序插入到a[0:i-1]中
}
}//insertSort
int main(int argc, char *argv[])
{
int a[6] = { 6, 5, 8, 4, 3, 1 };
cout << "原始陣列順序: ";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;
SortClass<int> SClass;
/*SClass.rearrange(a, 6);
cout << "採用附加陣列計數排序:";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;*/
/*SClass.selfrearrange(a, 6);
cout << "採用重排計數排序: ";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;*/
/*SClass.selectionSort(a, 6);
cout << "採用選擇排序: ";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;*/
/*SClass.selectionSortByOrder(a, 6);
cout << "採用及時終止選擇排序:";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;*/
/*SClass.bubbleSort(a, 6);
cout << "採用氣泡排序: ";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;*/
/*SClass.bubbleSortByOrder(a, 6);
cout << "採用及時終止氣泡排序:";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;*/
SClass.insertSort(a, 6);
cout << "採用插入排序: ";
for (int i = 0; i < 6; i++)
cout << a[i] << " ";
cout << endl;
return 0;
}