關聯分析之Apriori演算法
1.資料探勘與關聯分析
資料探勘是一個比較龐大的領域,它包括資料預處理(清洗去噪)、資料倉庫、分類聚類、關聯分析等。關聯分析可以算是資料探勘最貼近我們生活的一部分了,開啟卓越亞馬遜,當挑選一本《Android4高階程式設計》時,它會不失時機的列出你可能還會感興趣的書籍,比如Android遊戲開發、Cocos2d-x引擎等,讓你的購物車又豐富了些,而錢包又空了些。
關聯分析,即從一個數據集中發現項之間的隱藏關係。本篇文章Apriori演算法主要是基於頻繁集的關聯分析,所以本文中所出現的關聯分析預設都是指基於頻繁集的關聯分析。
有了一個感性的認識,我們來一段理性的形式化描述:
令項集I={i1,i2,...in}
且有一個數據集合D,它其中的每一條記錄T,都是I的子集
那麼關聯規則都是形如A->B的表示式,A、B均為I的子集,且A與B的交集為空
這條關聯規則的支援度:support = P(A並B)
這條關聯規則的置信度:confidence = support(A並B)/suport(A)
如果存在一條關聯規則,它的支援度和置信度都大於預先定義好的最小支援度與置信度,我們就稱它為強關聯規則。強關聯規則就可以用來了解項之間的隱藏關係。所以關聯分析的主要目的就是為了尋找強關聯規則,而Apriori演算法則主要用來幫助尋找強關聯規則。
注意:因為頻率=事件出現次數/總事件次數,為了方便,我們在以下都用事件出現的頻數而非頻率來作為支援度。
2.Apriori演算法描述
Apriori演算法指導我們,如果要發現強關聯規則,就必須先找到頻繁集。所謂頻繁集,即支援度大於最小支援度的項集。如何得到資料集合D中的所有頻繁集呢?
有一個非常土的辦法,就是對於資料集D,遍歷它的每一條記錄T,得到T的所有子集,然後計算每一個子集的支援度,最後的結果再與最小支援度比較。且不論這個資料集D中有多少條記錄(十萬?百萬?),就說每一條記錄T的子集個數({1,2,3}的子集有{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3},即如果記錄T中含有n項,那麼它的子集個數是2^n-1)。計算量非常巨大,自然是不可取的。
所以Aprior演算法提出了一個逐層搜尋的方法,如何逐層搜尋呢?包含兩個步驟:
1.自連接獲取候選集。第一輪的候選集就是資料集D中的項,而其他輪次的候選集則是由前一輪次頻繁集自連線得到(頻繁集由候選集剪枝得到)。
2.對於候選集進行剪枝。如何剪枝呢?候選集的每一條記錄T,如果它的支援度小於最小支援度,那麼就會被剪掉;此外,如果一條記錄T,它的子集有不是頻繁集的,也會被剪掉。
演算法的終止條件是,如果自連線得到的已經不再是頻繁集,那麼取最後一次得到的頻繁集作為結果。
需要值得注意的是:
Apriori演算法為了進一步縮小需要計算支援度的候選集大小,減小計算量,所以在取得候選集時就進行了它的子集是否有非頻繁集的判斷。(參見《資料探勘:概念與技術》一書)。
另外,兩個K項集進行連線的條件是,它們至少有K-1項相同。
知道了這些可以方便我們寫出高效的程式。
3.Apriori演算法例子推導
上面的描述是不是有點抽象,例子是最能幫助理解的良方。(假設最小支援度為2,最小置信度為0.6,最小支援度和置信度都是人定的,可以根據實驗結果的優劣對這兩個引數進行調整)
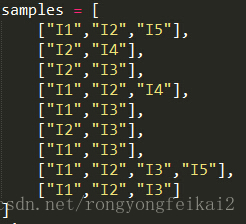
假設初始的資料集D如下:
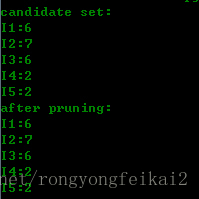
那麼第一輪候選集和剪枝的結果為:
可以看到,第一輪時,其實就是用的資料集中的項。而因為最小支援度是2的緣故,所以沒有被剪枝的,所以得到的頻繁集就與候選集相同。
第二輪的候選集與剪枝結果為:
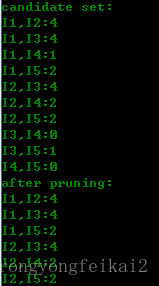
可以看到,第二輪的候選集就是第一輪的頻繁集自連線得到的(進行了去重),然後根據資料集D計算得到支援度,與最小支援度比較,過濾了一些記錄。頻繁集已經與候選集不同了。
第三輪候選集與頻繁集結果為:
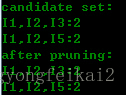
可以看到,第三輪的候選集發生了明顯的縮小,這是為什麼呢?
請注意取候選集的兩個條件:
1.兩個K項集能夠連線的兩個條件是,它們有K-1項是相同的。所以,(I2,I4)和(I3,I5)這種是不能夠進行連線的。縮小了候選集。
2.如果一個項集是頻繁集,那麼它不存在不是子集的頻繁集。比如(I1,I2)和(I1,I4)得到(I1,I2,I4),而(I1,I2,I4)存在子集(I1,I4)不是頻繁集。縮小了候選集。
第三輪得到的2個候選集,正好支援度等於最小支援度。所以,都算入頻繁集。
這時再看第四輪的候選集與頻繁集結果:
可以看到,候選集和頻繁集居然為空了!因為通過第三輪得到的頻繁集自連線得到{I1,I2,I3,I5},它擁有子集{I2,I3,I5},而{I2,I3,I5}不是頻繁集,不滿足:頻繁集的子集也是頻繁集這一條件,所以被剪枝剪掉了。所以整個演算法終止,取最後一次計算得到的頻繁集作為最終的頻繁集結果:
也就是:['I1,I2,I3', 'I1,I2,I5']
那麼,如何得到強規則呢?
比如對於:I1,I2,I3這個頻繁集,我們可以得到它的子集:{I1},{I2},{I3},{I1,I2},{I1,I3},{I2,I3},那麼可以得到的規則如下:
I1->I3^I2 0.333333333333
I2->I1^I3 0.285714285714
I3->I1^I2 0.333333333333
I1^I2->I3 0.5
I1^I3->I2 0.5
I2^I3->I1 0.5
左邊是規則,右邊是置信度。conf(I1->I3^I2) = support(I1,I2,I3)/support(I1)
與最小置信度相比較,我們就可以得到強規則了。
所以對於頻繁集['I1,I2,I3', 'I1,I2,I5']
我們得到的規則為:
I1->I3^I2 0.333333333333
I2->I1^I3 0.285714285714
I3->I1^I2 0.333333333333
I1^I2->I3 0.5
I1^I3->I2 0.5
I2^I3->I1 0.5
I1->I2^I5 0.333333333333
I2->I1^I5 0.285714285714
I5->I1^I2 1.0
I1^I2->I5 0.5
I1^I5->I2 1.0
I2^I5->I1 1.0
從而得到強規則為:
I5->I1^I2 : 1.0
I1^I5->I2 : 1.0
I2^I5->I1 : 1.0
意味著如果使用者買了商品I5,則極有可能買商品I1,I2;買了I1和I5,則極有可能買I2,如果買了I2,I5,則極有可能買I1。所以,你就知道在頁面上該如何推薦了。
4.Apriori演算法原始碼及輸出
為了加強對於Apriori演算法的瞭解,我用python寫了個簡單的程式(時間倉促,沒有考慮時間空間複雜度,也沒有非常嚴謹的測試正確性),希望以後能對此程式進行修改和優化。
演算法原始碼如下:
#coding:utf-8
samples = [
["I1","I2","I5"],
["I2","I4"],
["I2","I3"],
["I1","I2","I4"],
["I1","I3"],
["I2","I3"],
["I1","I3"],
["I1","I2","I3","I5"],
["I1","I2","I3"]
]
min_support = 2
min_confidence = 0.6
fre_list = list()
def get_c1():
global record_list
global record_dict
new_dict = dict()
for row in samples:
for item in row:
if item not in fre_list:
fre_list.append(item)
new_dict[item] = 1
else:
new_dict[item] = new_dict[item] + 1
fre_list.sort()
print "candidate set:"
print_dict(new_dict)
for key in fre_list:
if new_dict[key] < min_support:
del new_dict[key]
print "after pruning:"
print_dict(new_dict)
record_list = fre_list
record_dict = record_dict
def get_candidateset():
new_list = list()
#自連線
for i in range(0,len(fre_list)):
for j in range(0,len(fre_list)):
if i == j:
continue
#如果兩個k項集可以自連線,必須保證它們有k-1項是相同的
if has_samesubitem(fre_list[i],fre_list[j]):
curitem = fre_list[i] + ',' + fre_list[j]
curitem = curitem.split(",")
curitem = list(set(curitem))
curitem.sort()
curitem = ','.join(curitem)
#如果一個k項集要成為候選集,必須保證它的所有子集都是頻繁的
if has_infresubset(curitem) == False and already_constains(curitem,new_list) == False:
new_list.append(curitem)
new_list.sort()
return new_list
def has_samesubitem(str1,str2):
str1s = str1.split(",")
str2s = str2.split(",")
if len(str1s) != len(str2s):
return False
nums = 0
for items in str1s:
if items in str2s:
nums += 1
str2s.remove(items)
if nums == len(str1s) - 1:
return True
else:
return False
def judge(candidatelist):
# 計算候選集的支援度
new_dict = dict()
for item in candidatelist:
new_dict[item] = get_support(item)
print "candidate set:"
print_dict(new_dict)
#剪枝
#頻繁集的支援度要大於最小支援度
new_list = list()
for item in candidatelist:
if new_dict[item] < min_support:
del new_dict[item]
continue
else:
new_list.append(item)
global fre_list
fre_list = new_list
print "after pruning:"
print_dict(new_dict)
return new_dict
def has_infresubset(item):
# 由於是逐層搜尋的,所以對於Ck候選集只需要判斷它的k-1子集是否包含非頻繁集即可
subset_list = get_subset(item.split(","))
for item_list in subset_list:
if already_constains(item_list,fre_list) == False:
return True
return False
def get_support(item,splitetag=True):
if splitetag:
items = item.split(",")
else:
items = item.split("^")
support = 0
for row in samples:
tag = True
for curitem in items:
if curitem not in row:
tag = False
continue
if tag:
support += 1
return support
def get_fullpermutation(arr):
if len(arr) == 1:
return [arr]
else:
newlist = list()
for i in range(0,len(arr)):
sublist = get_fullpermutation(arr[0:i]+arr[i+1:len(arr)])
for item in sublist:
curlist = list()
curlist.append(arr[i])
curlist.extend(item)
newlist.append(curlist)
return newlist
def get_subset(arr):
newlist = list()
for i in range(0,len(arr)):
arr1 = arr[0:i]+arr[i+1:len(arr)]
newlist1 = get_fullpermutation(arr1)
for newlist_item in newlist1:
newlist.append(newlist_item)
newlist.sort()
newlist = remove_dumplicate(newlist)
return newlist
def remove_dumplicate(arr):
newlist = list()
for i in range(0,len(arr)):
if already_constains(arr[i],newlist) == False:
newlist.append(arr[i])
return newlist
def already_constains(item,curlist):
import types
items = list()
if type(item) is types.StringType:
items = item.split(",")
else:
items = item
for i in range(0,len(curlist)):
curitems = list()
if type(curlist[i]) is types.StringType:
curitems = curlist[i].split(",")
else:
curitems = curlist[i]
if len(set(items)) == len(curitems) and len(list(set(items).difference(set(curitems)))) == 0:
return True
return False
def print_dict(curdict):
keys = curdict.keys()
keys.sort()
for curkey in keys:
print "%s:%s"%(curkey,curdict[curkey])
# 計算關聯規則的方法
def get_all_subset(arr):
rtn = list()
while True:
subset_list = get_subset(arr)
stop = False
for subset_item_list in subset_list:
if len(subset_item_list) == 1:
stop = True
rtn.append(subset_item_list)
if stop:
break
return rtn
def get_all_subset(s):
from itertools import combinations
return sum(map(lambda r: list(combinations(s, r)), range(1, len(s)+1)), [])
def cal_associative_rule(frelist):
rule_list = list()
rule_dict = dict()
for fre_item in frelist:
fre_items = fre_item.split(",")
subitem_list = get_all_subset(fre_items)
for subitem in subitem_list:
# 忽略為為自身的子集
if len(subitem) == len(fre_items):
continue
else:
difference = set(fre_items).difference(subitem)
rule_list.append("^".join(subitem)+"->"+"^".join(difference))
print "The rule is:"
for rule in rule_list:
conf = cal_rule_confidency(rule)
print rule,conf
if conf >= min_confidence:
rule_dict[rule] = conf
print "The associative rule is:"
for key in rule_list:
if key in rule_dict.keys():
print key,":",rule_dict[key]
def cal_rule_confidency(rule):
rules = rule.split("->")
support1 = get_support("^".join(rules),False)
support2 = get_support(rules[0],False)
if support2 == 0:
return 0
rule_confidency = float(support1)/float(support2)
return rule_confidency
if __name__ == '__main__':
record_list = list()
record_dict = dict()
get_c1()
# 不斷進行自連線和剪枝,直到得到最終的頻繁集為止;終止條件是,如果自連線得到的已經不再是頻繁集
# 那麼取最後一次得到的頻繁集作為結果
while True:
record_list = fre_list
new_list = get_candidateset()
judge_dict = judge(new_list)
if len(judge_dict) == 0:
break
else:
record_dict = judge_dict
print "The final frequency set is:"
print record_list
# 根據頻繁集計算關聯規則
cal_associative_rule(record_list)演算法的輸出如下:
candidate set:
I1:6
I2:7
I3:6
I4:2
I5:2
after pruning:
I1:6
I2:7
I3:6
I4:2
I5:2
candidate set:
I1,I2:4
I1,I3:4
I1,I4:1
I1,I5:2
I2,I3:4
I2,I4:2
I2,I5:2
I3,I4:0
I3,I5:1
I4,I5:0
after pruning:
I1,I2:4
I1,I3:4
I1,I5:2
I2,I3:4
I2,I4:2
I2,I5:2
candidate set:
I1,I2,I3:2
I1,I2,I5:2
after pruning:
I1,I2,I3:2
I1,I2,I5:2
candidate set:
after pruning:
The final frequency set is:
['I1,I2,I3', 'I1,I2,I5']
The rule is:
I1->I3^I2 0.333333333333
I2->I1^I3 0.285714285714
I3->I1^I2 0.333333333333
I1^I2->I3 0.5
I1^I3->I2 0.5
I2^I3->I1 0.5
I1->I2^I5 0.333333333333
I2->I1^I5 0.285714285714
I5->I1^I2 1.0
I1^I2->I5 0.5
I1^I5->I2 1.0
I2^I5->I1 1.0
The associative rule is:
I5->I1^I2 : 1.0
I1^I5->I2 : 1.0
I2^I5->I1 : 1.0