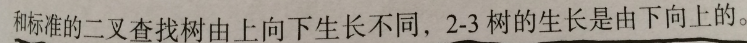本片部落格前面部分擷取自演算法(第4版)

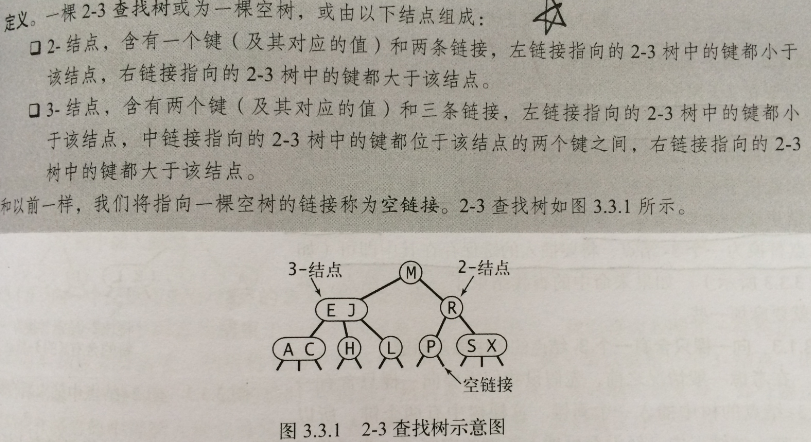
定義:

查詢:

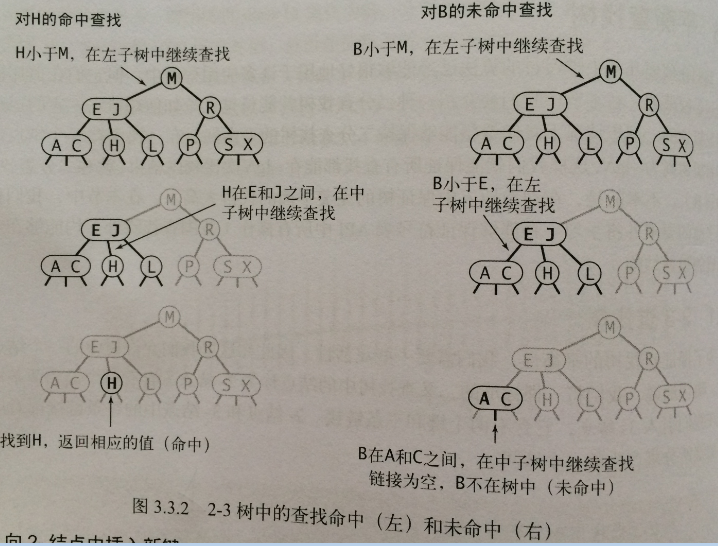
要判斷一個鍵是否存在樹中，先將它和根節點中的鍵比較，如果它和其中任意一個相等，查詢命中；否則就根據比較的結果找到指向相應區間的連線，並在其指向的子樹中遞迴地繼續查詢，如果找到了空連線上，查詢未命中。

插入:

插入之前，先要對2-3樹進行一次未命中的查詢:

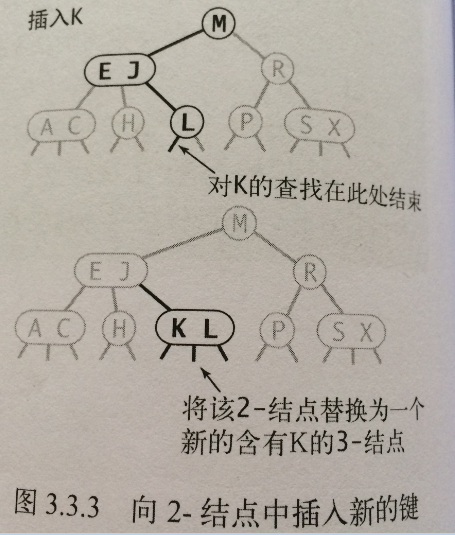
1、  向2-節點中插入新鍵

如果未命中查詢結束於一個2-節點，直接將2-節點替換為一個3-節點，並將要插入的鍵儲存在其中

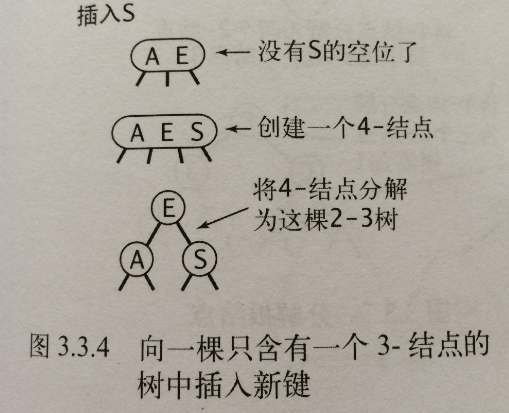
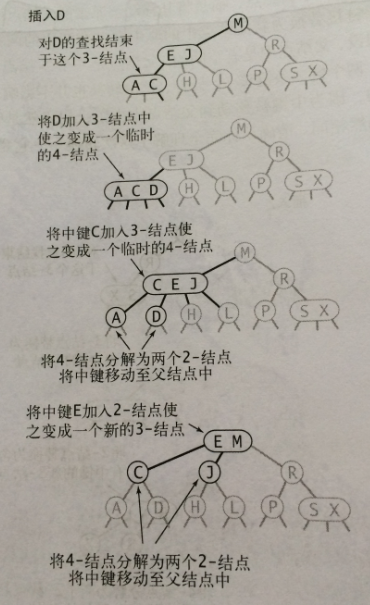
2、  向一顆只含3-節點的樹中插入新鍵

先臨時將新鍵存入唯一的3-節點中，使其成為一個4-節點，再將它轉化為一顆由3個2-節點組成的2-3樹，分解後樹高會增加1

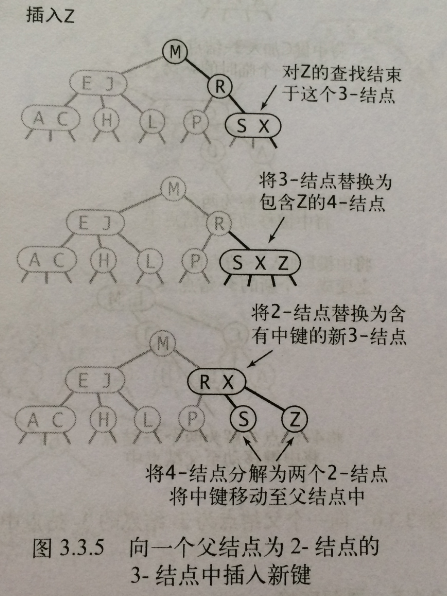
3、  向一個雙親節點為2-節點的3-節點中插入新鍵

先構造一個臨時的4-節點並將其分解，分解時將中鍵移動到雙親節點中(中鍵移動後，其雙親節點中的位置由鍵的大小確定)

4、  向一個雙親節點為3-節點的3-節點中插入新鍵

一直向上分解構造的臨時4-節點並將中鍵移動到更高層雙親節點，直到遇到一個-2節點並將其替換為一個不需要繼續分解的3-節點，或是到達樹根(3-節點)。

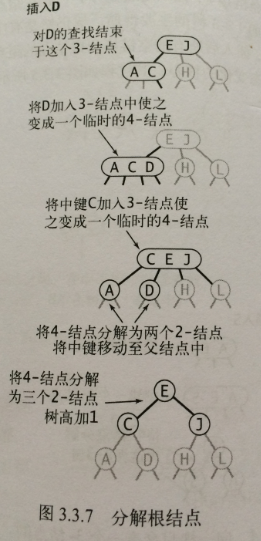
5、  分解根節點

如果從插入節點到根節點的路徑上全是3-節點，根將最終被替換為一個臨時的4-節點，將臨時的4-節點分解為3個2-節點，分解後樹高會增加1

變換:

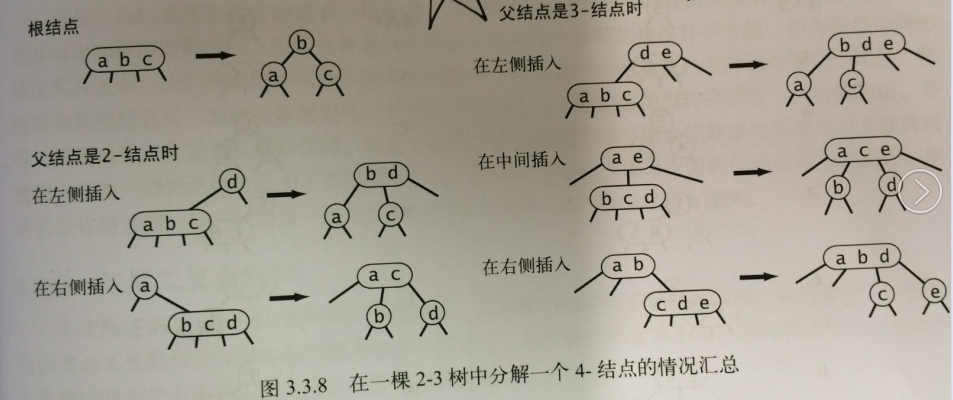
1、區域性變換

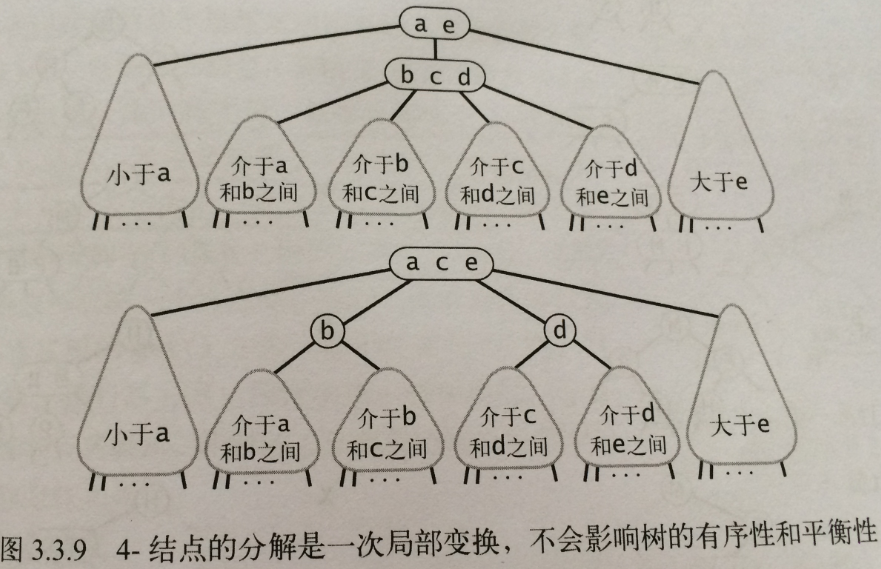
將對一個4-節點的分解叫做變換，對一個4-節點的變換方式可能有6種:

這些變換都是區域性的，除了相關的節點和連結之外不必修改或檢查樹的其他部分

2、全域性性質:

變換不會影響樹的全域性有序性和平衡性，任意空連結到根節點的路徑長度依舊是相等的

生長:

後面部分參考自大話資料結構

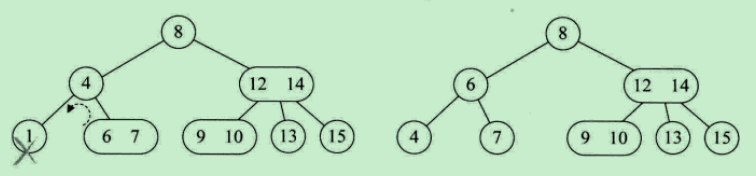
刪除:

插入之前，先要對2-3樹進行一次命中的查詢:

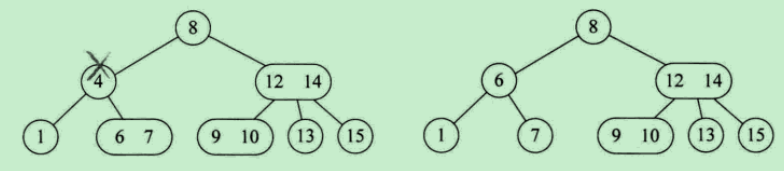
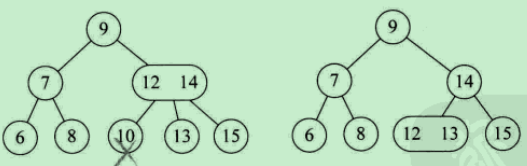
1、刪除非葉子節點key:

         使用中序遍歷下的直接後繼節點key來覆蓋當前節點key，再刪除用來覆蓋的後繼節點key

2、刪除葉子節點key:

a)        當前節點不是2-節點，直接刪除key

b)        當前節點是2-節點，刪除節點，並作一些判斷:

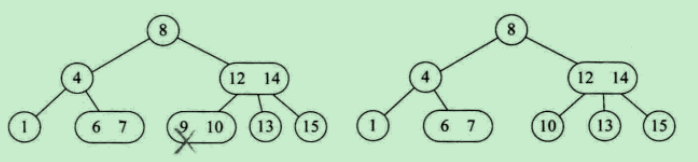
a)        當前節點的雙親節點是2-節點、兄弟節點是3-節點，將雙親節點移動到當前位置，再將兄弟節點中最接近當前位置的key移動到雙親節點中

b)        當前節點的雙親節點是2-節點、兄弟節點也是2-節點，先通過移動兄弟節點的中序遍歷直接後驅到兄弟節點，以使兄弟節點變為3-節點；再進行a)的操作

c)        當前節點的雙親節點是3-節點，拆分雙親節點使其成為2-節點，再將再將雙親節點中最接近的一個拆分key與中孩子合併，將合併後的節點作為當前節點

d)        2-3樹是一顆滿二叉樹，將2-3樹層樹減少，並將兄弟節點合併到雙親節點中，同時將雙親節點的所有兄弟節點合併到雙親節點的雙親節點中，如果生成了-4節點，再分解4-節點即可