淺析——B樹,B+樹,B*樹以及分析MySQL的兩種引擎
接觸到了資料結構當中的B樹,B+樹,B*樹,我覺得應該寫一篇部落格記錄下,畢竟是第一次接觸的,只有寫了部落格以後,感覺對這個的印象才會更加深刻。
前言:
為什麼要有B樹?
學習任何一個東西我們都要知道為什麼要有它,B樹也一樣,既然儲存資料,我們為什麼不用紅黑樹呢?
這個要從幾個方面來說了,
計算機有一個區域性性原理,就是說,當一個數據被用到時,其附近的資料也通常會馬上被使用。
所以當你用紅黑樹的時候,你一次只能得到一個鍵值的資訊,而用B樹,可以得到最多M-1個鍵值的資訊。這樣來說B樹當然更好了。
另外一方面,同樣的資料,紅黑樹的階數更大,B樹更短,這樣查詢的時候當然B樹更具有優勢了,效率也就越高。
一.B樹
首先我們來談一談關於B樹的問題,
對於B樹,我們首先要知道它的應用,B樹大量應用在資料庫和檔案系統當中。
B樹是對二叉查詢樹的改進。它的設計思想是,將相關資料儘量集中在一起,以便一次讀取多個數據,減少硬碟操作次數。
B樹為系統最優化大塊資料的讀和寫操作。B樹演算法減少定位記錄時所經歷的中間過程,從而加快存取速度。普遍運用在資料庫和檔案系統。
假定一個節點可以容納100個值,那麼3層的B樹可以容納100萬個資料,如果換成二叉查詢樹,則需要20層!假定作業系統一次讀取一個節點,並且根節點保留在記憶體中,那麼B樹在100萬個資料中查詢目標值,只需要讀取兩次硬碟。
B 樹可以看作是對2-3查詢樹的一種擴充套件,即他允許每個節點有M-1個子節點。
B樹的結構要求:
1)根節點至少有兩個子節點
2)每個節點有M-1個key,並且以升序排列
3)位於M-1和M key的子節點的值位於M-1 和M key對應的Value之間
4)其它節點至少有M/2個子節點
5)所有葉子節點都在同一層
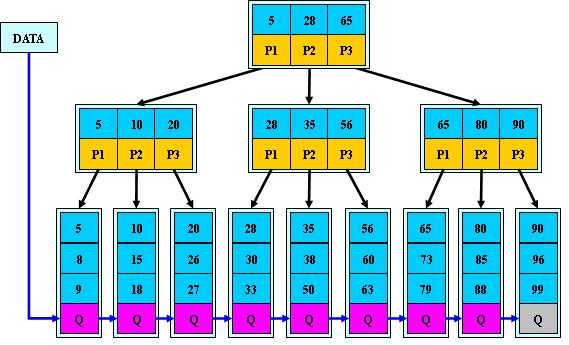
根據B樹的特點,我們首先可以寫出B樹的整體的結構。
1.B樹結構
B樹的結構我們定義需要參考規則,我們首先是需要給出儲存鍵值的一個數組,這個陣列的大小取決與我們定義的M,然後我們根據規則,可以得到一個儲存M+1個子的一個數組,然後當然為了方便訪問,parent指標,然後要有一個記錄每個節點中鍵值個數的一個size。
所以定義如下:
template <typename 2.B樹的查詢
對於AVL,BST,紅黑樹,B樹這些高階的資料結構而言,查詢演算法是非常重要的。我們首先確定返回值,對於這種關於key和key-value的資料結構,參考map和set,我們讓它返回一個pair的一個結構體。
pair結構體的定義在std中是
template<typename K,typename V>
struct pair
{
K key;
V value;
}我們只需要讓這個裡面的value變為bool值,value返回以後說明的是存不存就可以了。
接下來的思路就是從根節點進行和這個節點當中的每一個key比較,如果=那麼就返回找到了,如果小於,那麼就到這個節點左面的子節點中找,如果大了,就繼續向後面的鍵值進行查詢。如果相等那麼就返回。
示例程式碼:
pair <Node*,int > Find(const K &key)
{
Node* cur = _root;
Node* parent = NULL;
while (cur)
{
size_t i = 0;
while (i < cur->_size)
{
//如果小於當前,向後
if (cur->_keys[i] < key)
{
i++;
}
//如果大於,
else if (cur->_keys[i]>key)
{
cur = cur->_sub[i];
parent = cur;
break;
}
//相等,返回這個節點
else
{
return pair<Node *, int>(NULL, -1);
}
}
if (key > cur->_sub[i + 1])
{
cur = cur->_sub[i];
}
//為了防止出現我返回空指標操作,如果是空指標,那麼就返回父親
if (cur != NULL && i == cur->_size)
{
parent = cur;
cur = cur->_sub[i];
}
}
return pair<Node *, int>(parent, 1);
}3.B樹的插入
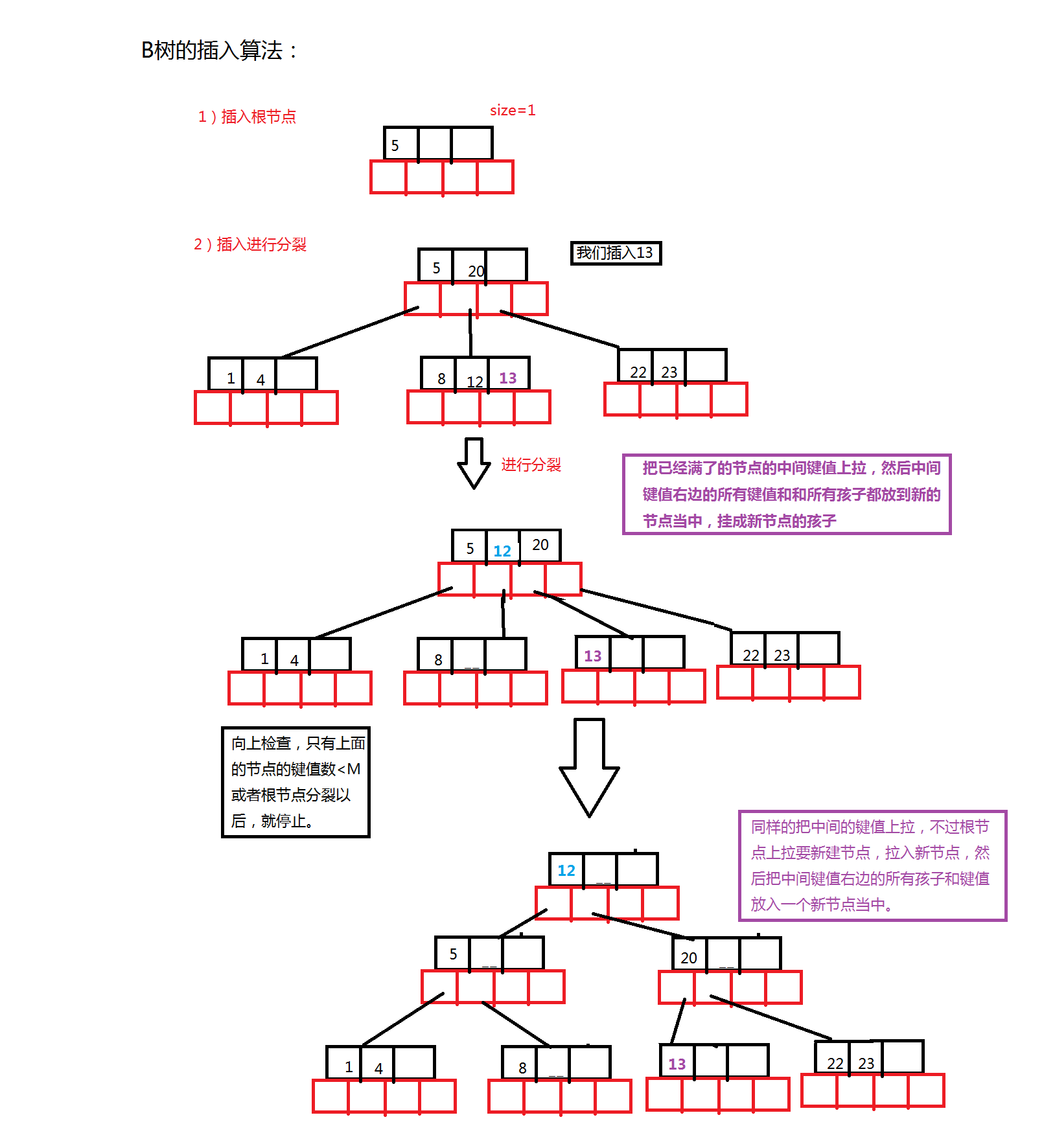
示例程式碼:
bool Insert(const K &key)
{
//首先來考慮空樹的情況
if (_root == NULL)
{
//給這個節點中新增key,並且讓size++。
_root = new Node;
_root->_keys[0] = key;
_root->_size++;
return true;
}
//使用通用的key-value結構體來儲存找到的key所在的節點。
pair<Node*,int > ret=Find(key);
//在這裡來看這個節點是否存在,存在就直接return false。
if (ret.second == -1)
{
return false;
}
Node* cur = ret.first;
K newKey = key;
Node *sub = NULL;
//此時表示考慮插入。
while (1)
{
//向cur裡面進行插入,如果沒滿插入,滿了就進行分裂。
InsetKey(cur, newKey, sub);
//小於M,這樣就可以直接插入
if (cur->_size < M)
{
return true;
}
//如果==M,那麼就應該進行分裂
//首先找到中間的節點
size_t mid = cur->_size / 2;
//建立一個節點,用來儲存中間節點右邊所有的節點和子節點。
Node * tmp = new Node;
size_t j = 0;
//進行移動sub以及所有的子接點。
for (size_t i = mid + 1; i < cur->_size; i++)
{
tmp->_keys[j] = cur->_keys[i];
cur->_keys[i] = K();
cur->_size--;
tmp->_size++;
j++;
}
//移動子串
for (j = 0; j < tmp->_size + 1; j++)
{
tmp->_sub[j] = cur->_sub[mid + 1 + j];
if (tmp->_sub[j])
{
tmp->_sub[j]->_parent = tmp;
}
cur->_sub[mid + 1 + j] = NULL;
}
//進行其他的移動
//分裂的條件就是要麼分裂根,要麼就是分裂子節點,要麼就是所在節點的節點數小於M。
//考慮根分裂,分裂的時候建立節點,然後把中間節點上拉,記得要更改最後的parent
if (cur->_parent == NULL)
{
_root = new Node();
_root->_keys[0] = cur->_keys[mid];
cur->_keys[mid] = K();
cur->_size--;
_root->_size++;
_root->_sub[0] = cur;
cur->_parent = _root;
_root->_sub[1] = tmp;
tmp->_parent = _root;
return true;
}
//分裂如果不是根節點,那麼就把mid節點插入到上一層節點中,然後看上一層節點是否要分裂。注意修改cur和sub
else
{
newKey = cur->_keys[mid];
cur->_keys[mid] = K();
cur->_size--;
cur = cur->_parent;
sub = tmp;
sub->_parent = cur;
}
}
}
void InsetKey(Node* cur, const K &key, Node* sub)
{
int i = cur->_size - 1;
while (i>=0)
{
//進行插入
if (key > cur->_keys[i])
{
break;
}
//進行移動
else
{
cur->_keys[i + 1] = cur->_keys[i];
cur->_sub[i + 2] = cur->_sub[i + 1];
}
i--;
}
//進行插入
cur->_keys[i + 1] = key;
//插入子
cur->_sub[i + 2] = sub;
//如果沒滿,只需要對size++;
if (cur->_size < M)
{
cur->_size++;
}
}二.B+樹
接下來介紹B樹的升級版本,
B+樹
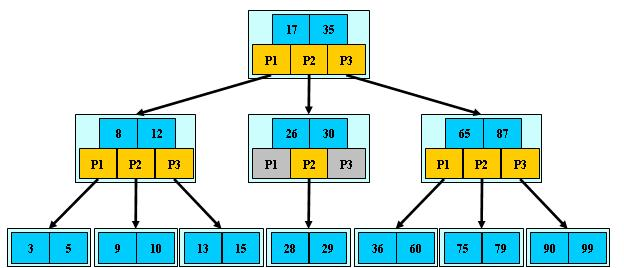
B+樹是B-樹的變體,也是一種多路搜尋樹:
1.其定義基本與B-樹同,除了:
2.非葉子結點的子樹指標與關鍵字個數相同;
3.非葉子結點的子樹指標P[i],指向關鍵字值屬於[K[i], K[i+1])的子樹(B-樹是開區間);
5.為所有葉子結點增加一個鏈指標;
6.所有關鍵字都在葉子結點出現;
B+樹相比於B樹能夠更加方便的遍歷。
B+樹簡單的說就是變成了一個索引一樣的東西。 B+的搜尋與B-樹也基本相同,區別是B+樹只有達到葉子結點才命中(B-樹可以在非葉子結點命中),B+樹的效能相當於是給葉子節點做一次二分查詢。
B+樹只有葉子節點存的是Key-value,非葉子節點只需要儲存key就好了。
B+樹的查詢演算法:當B+樹進行查詢的時候,你首先一定需要記住,就是B+樹的非葉子節點中並不儲存節點,只存一個鍵值方便後續的操作,所以非葉子節點就是索引部分,所有的葉子節點是在同一層上,包含了全部的關鍵值和對應資料所在的地址指標。這樣其實,進行 B+樹的查詢的時候,只需要在葉子節點中進行查詢就可以了。
B+樹的插入演算法與B樹的大致思想也是一樣的,只不過在這裡的上拉就是隻把鍵值上拉。
三.B*樹
接下來要說明的就是B*樹,B*樹是對B+樹進行的又一次的升級。在B+樹的非根和非葉子結點再增加指向兄弟的指標;
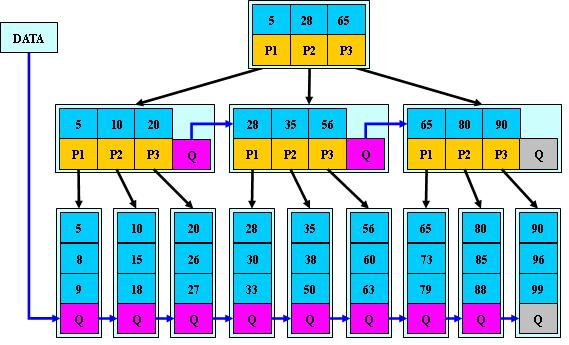
在B+樹基礎上,為非葉子結點也增加連結串列指標,將結點的最低利用率從1/2提高到2/3;
在這比如說當你進行插入節點的時候,它首先是放到兄弟節點裡面。如果兄弟節點滿了的話,進行分裂的時候從兄弟節點和這個節點各取出1/3,放入新建的節點當中,這樣也就實現了空間利用率從1/2到1/3。
四.關於B樹和B+樹相關應用拓展
其實B樹B+樹最需要關注的是它們的應用,B樹和B+樹經常被用於資料庫中,作為MySQL資料庫索引。索引(Index)是幫助MySQL高效獲取資料的資料結構。
為了查詢更加高效,所以採用B樹作為資料庫的索引。
在MySQL中,索引屬於儲存引擎級別的概念,不同 儲存引擎對索引的實現方式是不同的,我們接下來討論兩個引擎:MyISAM和InnoDB這兩種引擎。
1.MyISAM
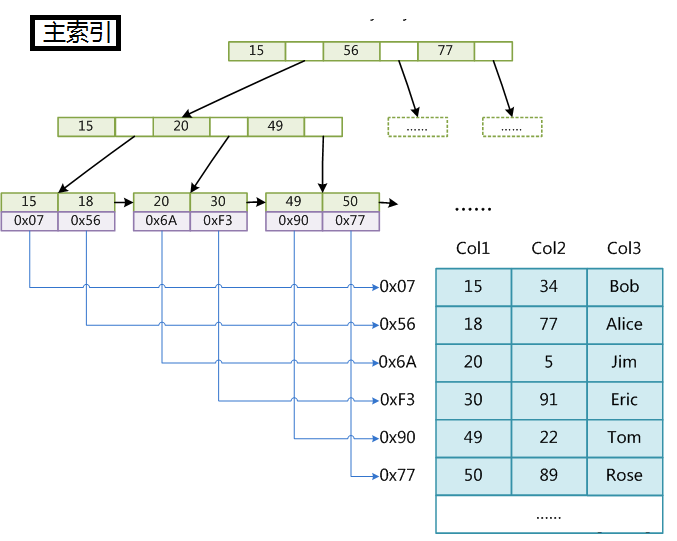
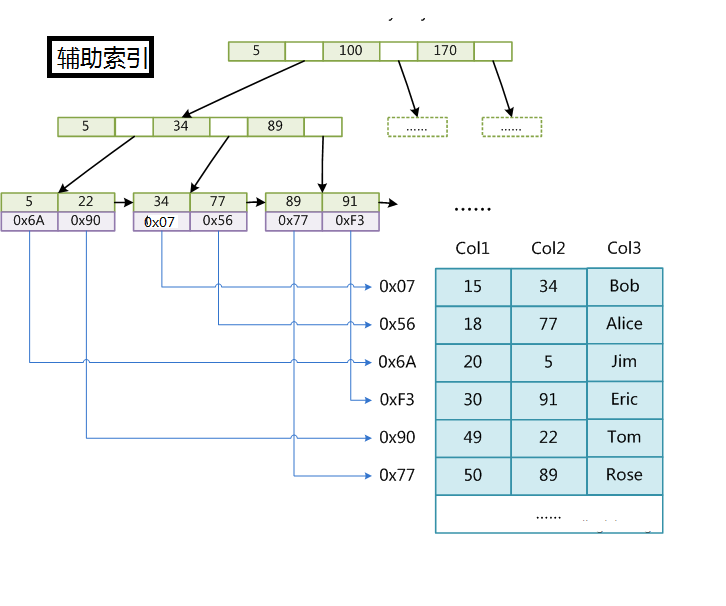
MyISAM中有兩種索引,分別是主索引和輔助索引,在這裡面的主索引使用具有唯一性的鍵值進行建立,而輔助索引中鍵值可以是相同的。MyISAM分別會存一個索引檔案和資料檔案。它的主索引是非聚集索引。當我們查詢的時候我們找到葉子節點中儲存的地址,然後通過地址我們找到所對應的資訊。
2.InnoDB
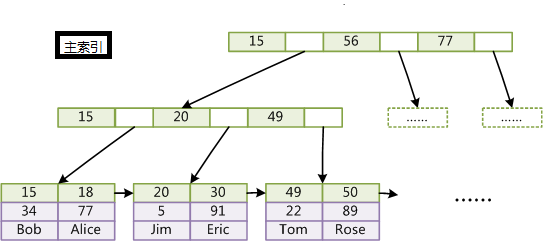
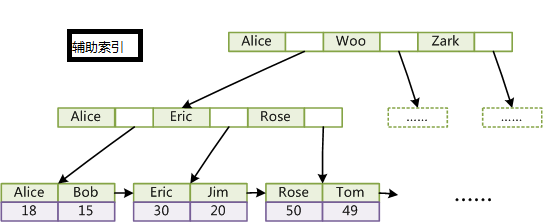
InnoDB索引和MyISAM最大的區別是它只有一個數據檔案,在InnoDB中,表資料檔案本身就是按B+Tree組織的一個索引結構,這棵樹的葉節點資料域儲存了完整的資料記錄。所以我們又把它的主索引叫做聚集索引。而它的輔助索引和MyISAM也會有所不同,它的輔助索引都是將主鍵作為資料域。所以,這樣當我們查詢的時候通過輔助索引要先找到主鍵,然後通過主索引再找到對於的主鍵,得到資訊。
這就是MySQL的兩種引擎
這兩種引擎那個好呢?
從歷史上來說MyISAM歷史更加久遠,所以InnoDB效能也就更好了,在這我們需要考慮當我們修改資料庫中的表的時候,資料庫發生了變化,那麼他們的主鍵的地址也就發生了變化,這樣你的MyISAM的主索引和輔助索引就需要進行重新建立索引。而InnoDB只需要改變主索引,因為它的輔助索引是存主鍵的。所以這樣考慮InnoDB更加高效。
另外,我們也就很容易明白為什麼不建議使用過長的欄位作為主鍵,因為所有輔助索引都引用主索引,過長的主索引會令輔助索引變得過大。