機器學習筆記1-基本概念
阿新 • • 發佈:2018-12-25
機器學習筆記1-基本概念
機器學習主要包括監督學習、非監督學習、半監督學習和強化學習等。實現方法包括模型、策略、演算法三個要素。
- 模型。在監督學習中,模型就是所要學習的條件概率分佈或決策函式。
- 策略。策略考慮的是按照什麼樣的準則學習或選擇最優的模型,即選擇損失函式。為了防止過擬合,一般會選擇正則化的損失函式。正則化項一般是模型複雜度的單調遞增函式,模型越複雜,正則化值就越大。比如,正則化項可以是模型引數向量的範數:
,此處L是損失函式, 是引數向量w的L1範數。 - 演算法。演算法是指學習模型的具體計算方法,即如何去求解該最優化問題。如梯度下降等演算法、最小二乘法等。
在監督學習中,主要包括三類問題:分類問題、標註問題和迴歸問題。
- 分類問題。當輸出變數Y取有限個離散值時,預測問題便成為分類問題。對應的輸入變數X可以是離散的,也可以是連續的。很多統計學習方法都可以用於分類,包括k近鄰法、感知機、樸素貝葉斯法、決策樹、邏輯迴歸、SVM、提升方法、貝葉斯網路、神經網路等。(這些演算法李航《統計學習方法》都有涉及)
- 標註問題。輸入變數是一個觀測序列,輸出變數是標記序列或狀態序列。常用的統計學習方法有隱馬爾可夫模型和條件隨機場。常見的例子有自然語言的詞性標註。
- 迴歸問題。迴歸用於預測輸入變數和輸出變數之間的關係。迴歸問題的學習等價於函式的擬合:選擇一條函式曲線使其很好地擬合已知資料且預測未知資料。迴歸學習最常用的損失函式是平方損失函式,在此情況下,迴歸問題可以由最小二乘法求解。
為了對學習器的泛化效能進行評估,需要一個測試集,然後以測試誤差作為泛化誤差的近似。測試集的獲取一般包括以下幾種方法:
- 留出法:直接將資料集劃分為兩個互斥的集合,一個作為訓練集,一個作為測試集。常見做法是2/3~4/5的樣本用於訓練,剩餘樣本用於測試。
- 交叉驗證法:將資料集劃分為k個大小相同的互斥子集。每次用k-1個子集作為訓練集,剩下的作為測試集。這樣就可獲得k組訓練/測試集,從而可進行k次訓練和測試,最終返回這k個測試結果的均值。(在堆疊泛化過程中,交叉驗證法返回的結果不是均值,是另外一種組合的形式)當k值等於資料集的樣本數m時,即為“留一法”。
- 自助法:對給定m個樣本的資料集D,每次從D中選一個樣本,拷貝放入D’,然後再將該樣本放回D中。重複執行該過程m次,便得到了包含m個樣本的資料集D’。(這種做法在隨機森林中會用到)自助法會改變初始資料集的分佈,這會引入估計偏差。
有了測試集,有了泛化誤差後,可將其分解為偏差、方差、噪聲之和。偏差度量了演算法的預測與真實結果的偏離程度,即刻畫了演算法本身的擬合能力;方差度量了訓練集的變動所導致的學習效能的變化,即刻畫了資料擾動所造成的影響;噪聲則刻畫了當前任務人和演算法所能達到的期望泛化誤差的下界,即刻畫了學習問題本身的難度。
補充:
最小二乘法
最小二乘法的核心思想是,通過最小化誤差的平方和,使得擬合物件無限接近目標物件。除了“殘差平方和最小”這條標準外,還有另外兩條標準:
(1) 用“殘差和最小”作為標準。但很快發現計算“殘差和”存在相互抵消的問題。
(2) 用“殘差絕對值和最小”作為標準。但絕對值的計算比較麻煩。
其實從範數的角度考慮這個問題,絕對值和對應的是1範數,平方和對應的就是2範數。從距離角度考慮,絕對值和對應的是曼哈頓距離,平方和對應的就是歐氏距離。假設擬合函式具有如下形式:
(1)
對於方程(1)中的引數向量
,根據其線性形式與非線性形式,最小二乘法又可以分為線性和非線性兩種。
- 對於線性最小二乘法,方程(1)可寫為:
(2)
令
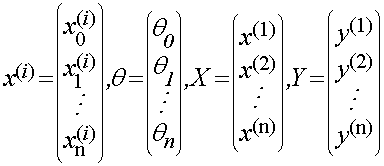
殘差函式
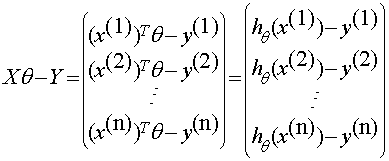
殘差和
對 求導,經過一系列推導,可得到
令偏導數為零,可求得極值點
此即為線性最小二乘的解法。 - 對於非線性最小二乘法,通常無法直接寫出其導數形式(函式過於複雜),無法找到全域性最小值。因此需要通過不斷地迭代尋找區域性最小值。有兩種通用的演算法:
- 下降法。通過一個初值,不斷地求解下降方向(函式負梯度方向),設定合理的步長,求解得到一些列的中間值,最後收斂到某個區域性最小值。(神經網路的後向傳輸與此相似)
- 高斯牛頓法。該演算法的基本思想是將函式 進行一階泰勒展開 ,其中 為函式的雅克比矩陣,即函式 的一階導。此時,目標函式展開為 。對其求導並令其為零,可得
