Redis中支援的資料結構比Memcached要多，如基本的字串、雜湊表、列表、集合、可排序集，在這些基本資料結構上也提供了針對該資料結構的各種操作，這也是Redis之所以流行起來的一個重要原因,當然Redis能夠流行起來的原因，遠遠不只這一個,如支援高併發的讀寫、資料的持久化、高效的記憶體管理及淘汰機制...

從Redis的git提交歷史中，可以查到，2009/10/24在1.050版本，Redis開始支援可排序集,在該版本中，只提供了一條命令zadd,巨集定義如下所示:

1     {"zadd",zaddCommand,4,REDIS_CMD_BULK|REDIS_CMD_DENYOOM},

那麼什麼是可排序集呢? 從Redis 1.0開始就給我們提供了集合(Set)這種資料結構，集合就跟數學上的集合概念是一個道理【無序性，確定性，互異性】,集合裡的元素無法保證元素的順序，而業務上的需求，可能不止是一個集合，而且還要求能夠快速地對集合元素進行排序，於是乎，Redis中提供了可排序集這麼一種資料結構，似乎也是合情合理,無非就是在集合的基礎上增加了排序功能,也許有人會問，Redis中不是有Sort命令嘛，下面的操作不也是同樣可以達到對無序集的排序功能嘛，是的,是可以，但是在這裡我們一直強調的是快速這兩個字，而Sort命令的時間複雜度為O(N+M*Log(M)),可排序集獲取一定範圍內元素的時間複雜度為O(log(N) + M)

[email protected]:/home/bjpengpeng/redis-3.0.1/src# ./redis-cli 
127.0.0.1:6379> sort set
1) "1"
2) "2"
3) "3"
4) "5"
127.0.0.1:6379> sort set desc
1) "5"
2) "3"
3) "2"
4) "1"
127.0.0.1:6379>

在瞭解可排序集是如何實現之前，需要了解一種資料結構跳錶(Skip List),跳錶與AVL、紅黑樹...等相比，資料結構簡單，演算法易懂，但查詢的時間複雜度與平衡二叉樹/紅黑樹相當,跳錶的基本結構如下圖所示

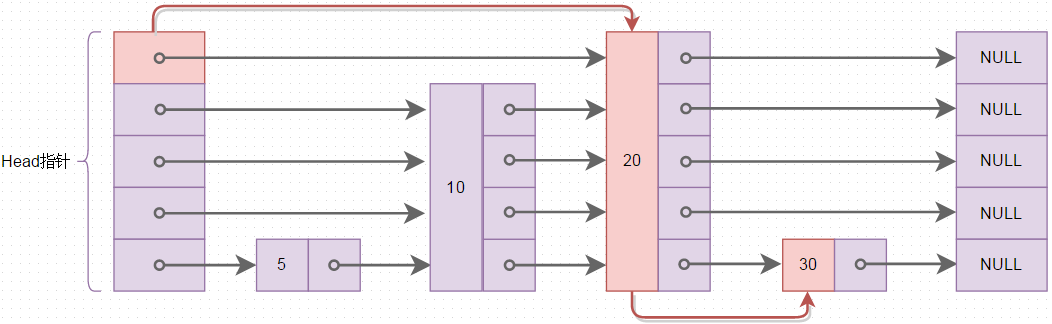
上圖中整個跳錶結構存放了4個元素5->10->20->30,圖中的紅色線表示查詢元素30時，走的查詢路線,從Head指標數組裡最頂層的指標所指的20開始比較，與普通的連結串列查詢相比，跳錶的查詢可以跳躍元素，上圖中查詢30，發現30比20大，則查詢就是20開始，而普通連結串列的查詢必須一個元素一個元素的比較，時間複雜度為O(n)

有了上圖所示的跳錶基本結構，再看看如何向跳錶中插入元素，向跳錶中插入元素，由於元素所在層級的隨機性，平均起來也是O(logn)，說白了，就是查詢元素應該插入在什麼位置，然後就是普通的移動指標問題，再想想往有序單鏈表的插入操作吧，時間複雜度是不是也是O(n),下圖所示是往跳錶中插入元素28的過程,圖中紅色線表示查詢插入位置的過程，綠色線表示進行指標的移動，將該元素插入

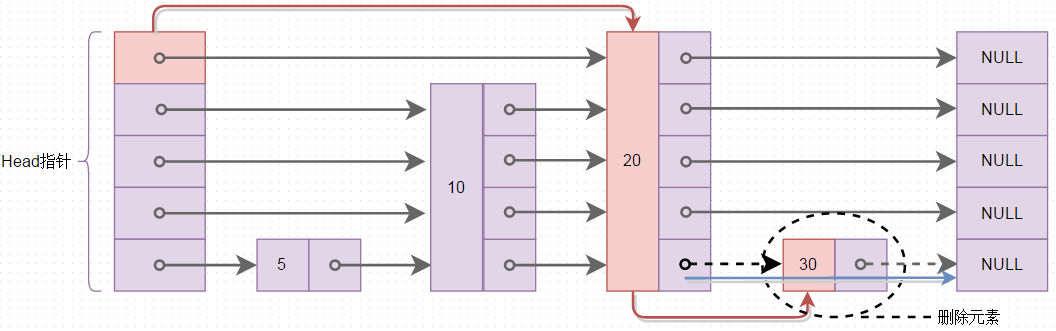
有了跳錶的查詢及插入那麼就看看在跳錶中如何刪除元素吧，跳錶中刪除元素的個程，查詢要刪除的元素，找到後，進行指標的移動，過程如下圖所示，刪除元素30

有了上面的跳錶基本結構圖及原理，自已設計及實現跳錶吧，這樣當看到Redis裡面的跳錶結構時我們會更加熟悉，更容易理解些,【下面是對Redis中的跳錶資料結構及相關程式碼進行精減後形成的可執行程式碼】,首先定義跳錶的基本資料結構如下所示

在程式碼中我們定義了跳錶結構中儲存的資料為Key->Value這種形式的鍵值對，注意的是skiplistNode裡面內含了一個結構體,代表的是層級，並且定義了跳錶的最大層級為32級,下面的程式碼是建立空跳錶，以及層級的獲取方式

在這段程式碼中，使用了隨機函式獲取過元素所在的層級，下面就是重點，向跳錶中插入元素，插入元素之前先查詢插入的位置,程式碼如下所示，程式碼中注意update[i]

下面是程式碼中刪除節點的操作，和插入節點類似

最後，附上一個不優雅的測試樣例

有了上面的跳錶理論基礎，理解Redis中跳錶的實現就不是那麼難了

Redis中跳錶的基本資料結構定義如下，與基本跳錶資料結構相比，在Redis中實現的跳錶其特點是不僅有前向指標，也存在後向指標，而且在前向指標的結構中存在span跨度欄位，這個跨度欄位的出現有助於快速計算元素在整個集合中的排名

//定義跳錶的基本資料節點
typedef struct zskiplistNode {
    robj *obj; // zset value
    double score;// zset score
    struct zskiplistNode *backward;//後向指標
    struct zskiplistLevel {//前向指標
        struct zskiplistNode *forward;
        unsigned int span;
    } level[];
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

//有序集資料結構
typedef struct zset {
    dict *dict;//字典存放value,以value為key
    zskiplist *zsl;
} zset;

將如上資料結構轉化成更形式化的圖形表示，如下圖所示

在上圖中，可以看到header指標指向的是一個具有固定層級(32層)的表頭節點,為什麼定義成32,是因為定義成32層理論上對於2^32-1個元素的查詢最優，而2^32=4294967296個元素，對於絕大多數的應用來說，已經足夠了，所以就定義成了32層,到於為什麼查詢最優，你可以將其想像成一個32層的完全二叉排序樹，算算這個樹中節點的數量

Redis中有序集另一個值得注意的地方就是當Score相同的時候，是如何儲存的，當集合中兩個值的Score相同，這時在跳錶中儲存會比較這兩個值，對這兩個值按字典排序儲存在跳錶結構中

有了上述的資料結構相關的基礎知識，來看看Redis對zskiplist/zskiplistNode的相關操作,原始碼如下所示(原始碼均出自t_zset.c)

建立跳錶結構的原始碼

//#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;
    //分配記憶體
    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;//預設層級為1
    zsl->length = 0;//跳錶長度設定為0
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        //因為沒有任何元素，將表頭節點的前向指標均設定為0
        zsl->header->level[j].forward = NULL;
        //將表頭節點前向指標結構中的跨度欄位均設為0
        zsl->header->level[j].span = 0;
    }
    //表頭後向指標設定成0
    zsl->header->backward = NULL;
    //表尾節點設定成NULL
    zsl->tail = NULL;
    return zsl;
}

在上述程式碼中呼叫了zslCreateNode這個函式,函式的原始碼如下所示=

zskiplistNode *zslCreateNode(int level, double score, robj *obj) {
    zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    zn->score = score;
    zn->obj = obj;
    return zn;
}

執行完上述程式碼之後會建立如下圖所示的跳錶結構

建立了跳錶的基本結構，下面就是插入操作了，Redis中原始碼如下所示

zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; //update[32]
    unsigned int rank[ZSKIPLIST_MAXLEVEL];//rank[32]
    int i, level;
    redisAssert(!isnan(score));
    x = zsl->header;
    //尋找元素插入的位置 
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
            (x->level[i].forward->score < score || //以下是得分相同的情況下，比較value的字典排序
                (x->level[i].forward->score == score &&compareStringObjects(x->level[i].forward->obj,obj) < 0))) {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    //產生隨機層數
    level = zslRandomLevel();
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        //記錄最大層數
        zsl->level = level;
    }
    //產生跳錶節點
    x = zslCreateNode(level,score,obj);
    for (i = 0; i < level; i++) {
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;
        //更新跨度
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }
    //此種情況只會出現在隨機出來的層數小於最大層數時
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}

上述原始碼中，有一個產生隨機層數的函式，原始碼如下所示:

int zslRandomLevel(void) {
    int level = 1;
    //#define ZSKIPLIST_P 0.25 
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    //#ZSKIPLIST_MAXLEVEL 32
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

圖形化的形式描述如下圖所示:

理解了插入操作，其他查詢，刪除，求範圍操作基本上類似