時間複雜度&空間複雜度分析
阿新 • • 發佈:2018-12-25
時間複雜度:
一般情況下,演算法中基本操作重複執行的次數是問題規模n的某個函式f(n),進而分析f(n)隨n的變化情況並確定T(n)的數量級。這裡用"O"來表示數量級,給出演算法的時間複雜度。
T(n)=O(f(n));
它表示隨著問題規模的n的增大,演算法的執行時間的增長率和f(n)的增長率相同,這稱作演算法的漸進時間複雜度,簡稱時間複雜度。而我們一般討論的是最壞時間複雜度,這樣做的原因是:最壞情況下的時間複雜度是演算法在任何輸入例項上執行時間的上界,分析最壞的情況以估算演算法指向時間的一個上界。
時間複雜度的分析方法:
1、時間複雜度就是函式中基本操作所執行的次數 
空間複雜度: 演算法的空間複雜度並不是計算實際佔用的空間,而是計算整個演算法的輔助空間單元的個數,
例: 1、求二分法的時間複雜度和空間複雜度。 非遞迴:
分析:
迴圈的基本次數是log2 N,所以: 時間複雜度是O(log2 N); 由於輔助空間是常數級別的所以: 空間複雜度是O(1); 遞迴:

遞迴的次數和深度都是log2 N,每次所需要的輔助空間都是常數級別的: 時間複雜度:O(log2 N) 空間複雜度:O(log2N ) 2、斐波那契數列的時間和空間複雜度 //遞迴情況下的斐波那契數列
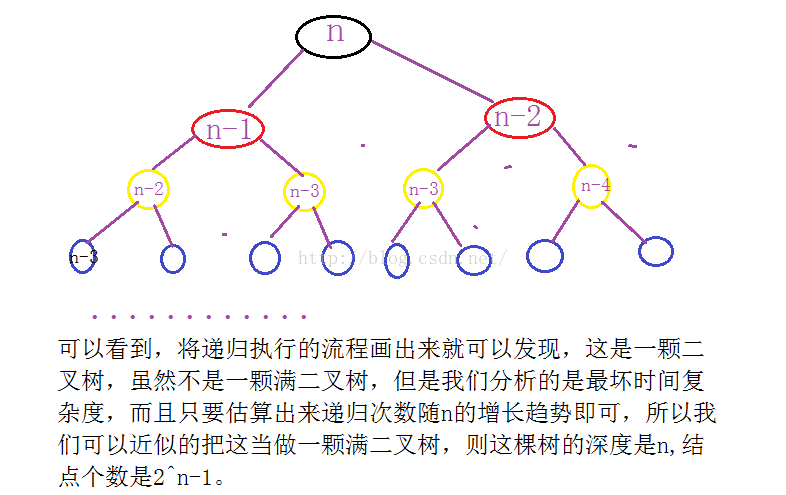
遞迴的時間複雜度是: 遞迴次數*每次遞迴中執行基本操作的次數 所以時間複雜度是: O(2^N) 遞迴的空間複雜度是: 遞迴的深度*每次遞迴所需的輔助空間的個數 所以空間複雜度是:O(N) //求前n項中每一項的斐波那契數列的值
迴圈的基本操作次數是n-1,輔助空間是n+1,所以: 時間複雜度O(n) 空間複雜度O(n) //非遞迴
迴圈的基本次數是n-1,所用的輔助空間是常數級別的: 時間複雜度:O(n) 空間複雜度:O(1)

空間複雜度: 演算法的空間複雜度並不是計算實際佔用的空間,而是計算整個演算法的輔助空間單元的個數,
例: 1、求二分法的時間複雜度和空間複雜度。 非遞迴:
template<typename T> T* BinarySearch(T* array,int number,const T& data) { assert(number>=0); int left = 0; int right = number-1; while (right >= left) { int mid = (left&right) + ((left^right)>>1); if (array[mid] > data) { right = mid - 1; } else if (array[mid] < data) { left = mid + 1; } else { return (array + mid); } } return NULL; }
分析:

迴圈的基本次數是log2 N,所以: 時間複雜度是O(log2 N); 由於輔助空間是常數級別的所以: 空間複雜度是O(1); 遞迴:
template<typename T>
T* BinarySearch(T* left,T* right,const T& data)
{
assert(left);
assert(right);
if (right >=left)
{
T* mid =left+(right-left)/2;
if (*mid == data)
return mid;
else
return *mid > data ? BinarySearch(left, mid - 1, data) : BinarySearch(mid + 1, right, data);
}
else
{
return NULL;
}
}
遞迴的次數和深度都是log2 N,每次所需要的輔助空間都是常數級別的: 時間複雜度:O(log2 N) 空間複雜度:O(log2N ) 2、斐波那契數列的時間和空間複雜度 //遞迴情況下的斐波那契數列
long long Fib(int n)
{
assert(n >= 0);
return n<2 ? n : Fib(n - 1) + Fib(n-2);
}
遞迴的時間複雜度是: 遞迴次數*每次遞迴中執行基本操作的次數 所以時間複雜度是: O(2^N) 遞迴的空間複雜度是: 遞迴的深度*每次遞迴所需的輔助空間的個數 所以空間複雜度是:O(N) //求前n項中每一項的斐波那契數列的值
long long *Fib(int n)
{
assert(n>=0);
long long *array = new long long[n + 1];
array[0] = 0;
if (n > 0)
{
array[1] = 1;
}
for (int i = 2; i <n+1; i++)
{
array[i] = array[i - 1] + array[i - 2];
}
return array;
}迴圈的基本操作次數是n-1,輔助空間是n+1,所以: 時間複雜度O(n) 空間複雜度O(n) //非遞迴
long long Fib(int n)
{
assert(n >= 0);
long long first=0,second=1;
for (int i = 2; i <= n; i++)
{
first = first^second;
second = first^second;
first = first^second;
second = first + second;
}
return second;
}迴圈的基本次數是n-1,所用的輔助空間是常數級別的: 時間複雜度:O(n) 空間複雜度:O(1)
