二叉樹的基本操作 C++程式碼實現
阿新 • • 發佈:2018-12-25
首先定義節點
typedef struct BTree
{
int value;
struct BTree *lchild;
struct BTree *rchild;
}BTree;前序遞迴建立二叉樹
/*
**num 前序序列
**index 下標
*/
BTree *CreateBTree(BTree *node,int *num,int& index)
{
if(num[index] == 0)
return NULL;
else
{
node = new BTree;
node -> value = num[index 幾種遍歷
遞迴--前序遍歷
void preOrder(BTree * root)
{
if(root == NULL)
return;
cout << root -> value << 非遞迴--前序遍歷
void preOrder_dxm(BTree * root)
{
stack<BTree*> S;
BTree *p = root;
while(p != NULL || !S.empty())
{
while(p != NULL)
{
cout 遞迴--中序遍歷
void inOrder(BTree * root)
{
if(root == NULL)
return;
inOrder(root -> lchild);
cout << root -> value << " ";
inOrder(root -> rchild);
}非遞迴--中序遍歷
void inOrder_dxm(BTree * root)
{
stack<BTree*> S;
BTree *p = root;
while(p != NULL || !S.empty())
{
while(p != NULL)
{
//cout << p -> value << " ";
S.push(p);
p = p -> lchild;
}
if(!S.empty())
{
p = S.top();
cout << p -> value << " ";
S.pop();
if(S.empty())
return ;
//S.pop();
p = S.top();
cout << p -> value << " ";
S.pop();
p = p -> rchild;
}
}
}遞迴--後序遍歷
void postOrder(BTree * root)
{
if(root == NULL)
return;
postOrder(root -> lchild);
postOrder(root -> rchild);
cout << root -> value << " ";
}非遞迴--後序遍歷
void postOrder_dxm(BTree * root)
{
stack<BTree*> S;
BTree *cur;
BTree *pre = NULL;
S.push(root);
while(!S.empty())
{
cur = S.top();
if((cur -> lchild == NULL && cur -> rchild == NULL) ||
(pre != NULL && (pre == cur -> lchild || pre == cur ->rchild)))
{
cout << cur -> value << " ";
S.pop();
pre = cur;
}
else
{
if(cur -> rchild != NULL)
S.push(cur -> rchild);
if(cur -> lchild != NULL)
S.push(cur -> lchild);
}
}
}求二叉樹的深度
int getdepth(BTree *root)
{
if(root == NULL)
return 0;
int lchild_depth = getdepth(root -> lchild);
int rchild_depth = getdepth(root -> rchild);
return max(lchild_depth,rchild_depth) + 1;
}求二叉樹葉子節點的個數
int getleaves(BTree *root)
{
if(root == NULL)
return 0;
if(root -> lchild == NULL && root -> rchild == NULL)
return 1;
return 1 + getleaves(root -> lchild) + getleaves(root -> rchild);
}樹狀列印二叉樹
void print(BTree *root,int h)
{
if(root != NULL)
{
print(root -> rchild,h+1);
for(int i=0; i<h; i++)
cout << " ";
cout << root -> value;
print(root -> lchild,h+1);
}
cout << endl;
}主函式
int main()
{
int num[] = {1,2,4,8,0,0,9,0,0,5,10,0,0,11,0,0,3,6,12,0,0,13,0,0,7,14,0,0,15,0,0};
BTree *root = NULL;
int index = 0;
root = CreateBTree(root,num,index);
cout << "前序非遞迴遍歷: " << endl;
preOrder_dxm(root);
cout << endl;
cout << "中序遞迴遍歷: " << endl;
inOrder_dxm(root);
cout << endl;
cout << "後續非遞迴遍歷: " << endl;
postOrder_dxm(root);
cout << endl << endl;;
cout << "此二叉樹的形狀為: " << endl;
print(root,1);
return 0;
}輸出結果
由給定二叉樹的兩種序列建立二叉樹
前序序列:根在前,且左孩子在右孩子前
中序序列:根在中間,左邊為左孩子,右邊為右孩子
後序序列:根在最後,且左孩子在右孩子前
根據二叉樹前序序列和中序序列建立二叉樹:
- 前序序列的第一個元素就是二叉樹的根節點
- 在中序序列中找到根節點,根據根節點將中序序列分為兩部分:此節點左邊的是左子樹的中序序列,右邊是右子樹的中序序列;
- 將除去根節點的前序序列分為兩部分:左子樹在前,剩下為右子樹
- 遞迴建立左右子樹
/*************************************************************************
> File Name: 中序&先序建立二叉樹.cpp
> Author: Tanswer
> Mail: [email protected]
> Created Time: 2016年10月24日 星期一 17時33分24秒
************************************************************************/
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
typedef struct BTree
{
char value;
struct BTree *lchild;
struct BTree *rchild;
}BTree;
BTree *Created(BTree *root,string pre,string in)
{
if(pre.length() == 0)
{
root = NULL;
return NULL;
}
//前序的第一個值 為 根
int root_value = pre[0];
//找到根在中序中的位置 :下標
int index = in.find(root_value);
//左孩子的中序序列
string lchild_in = in.substr(0,index);
//右孩子的中序序列
string rchild_in = in.substr(index+1);
//左孩子結點個數
int lchild_length = lchild_in.length();
//右孩子結點個數
int rchild_length = rchild_in.length();
//左孩子的前序序列
string lchild_pre = pre.substr(1,lchild_length);
//右孩子的前序序列
string rchild_pre = pre.substr(1+lchild_length);
root = new BTree;
if(root != NULL)
{
root -> value = root_value;
//root -> lchild = new BTree;
root -> lchild = Created(root -> lchild,lchild_pre,lchild_in);
//root -> rchild = new BTree;
root -> rchild = Created(root -> rchild,rchild_pre,rchild_in);
}
return root;
}
/*樹狀列印二叉樹*/
void print(BTree *root,int h)
{
if(root != NULL)
{
print(root -> rchild,h+1);
for(int i=0; i<h; i++)
cout << " ";
cout << root -> value;
print(root -> lchild,h+1);
}
cout << endl;
}
int main()
{
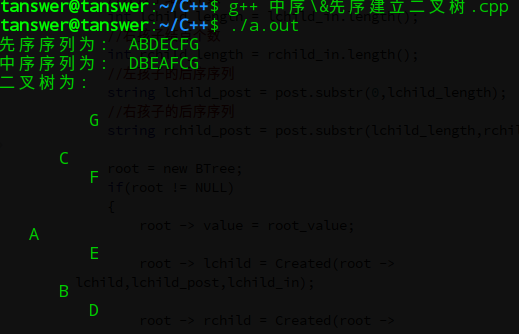
cout << "先序序列為: ABDECFG" << endl;
cout << "中序序列為: DBEAFCG" << endl;
cout << "二叉樹為: " << endl;;
string pre = "ABDECFG";
string in = "DBEAFCG";
BTree *root = NULL;
root = Created(root,pre,in);
print(root,1);
return 0;
}輸出結果:
根據二叉樹後序序列和中序序列建立二叉樹:
過程和上面的類似,就不再寫了,直接上程式碼
BTree *Created(BTree *root,string post,string in)
{
if(post.length() == 0)
{
root = NULL;
return NULL;
}
/*後序序列的結點個數*/
int size = post.size();
//後序的最後一個值 為 根
int root_value = post[size - 1];
//找到根在中序中的位置 :下標
int index = in.find(root_value);
//左孩子的中序序列
string lchild_in = in.substr(0,index);
//右孩子的中序序列
string rchild_in = in.substr(index+1);
//左孩子結點個數
int lchild_length = lchild_in.length();
//右孩子結點個數
int rchild_length = rchild_in.length();
//左孩子的後序序列
string lchild_post = post.substr(0,lchild_length);
//右孩子的後序序列
string rchild_post = post.substr(lchild_length,rchild_length);
root = new BTree;
if(root != NULL)
{
root -> value = root_value;
root -> lchild = Created(root -> lchild,lchild_post,lchild_in);
root -> rchild = Created(root -> rchild,rchild_post,rchild_in);
}
return root;
}