1.B-Tree定義

在電腦科學中，B樹（英語：B-tree）是一種自平衡的樹，能夠保持資料有序。這種資料結構能夠讓查詢資料、順序訪問、插入資料及刪除的動作，都在對數時間內完成。

2.為什麼引入B-Tree?

首先，包括紅黑樹是將輸入存入記憶體的一種內部查詢樹。

而B樹是前面平衡樹演算法的擴充套件，它支援儲存在磁碟或者網路上的符號表進行外部查詢，這些檔案可能比我們以前考慮的輸入要大的多（難以存入記憶體）。

既然內容儲存在磁碟中，那麼自然會因為樹的深度過大而造成磁碟I/O讀寫過於頻繁（磁碟讀寫速率是有限制的），進而導致查詢效率低下。

那麼降低樹的深度自然很重要了。因此，我們引入了B樹，平衡多路查詢樹。

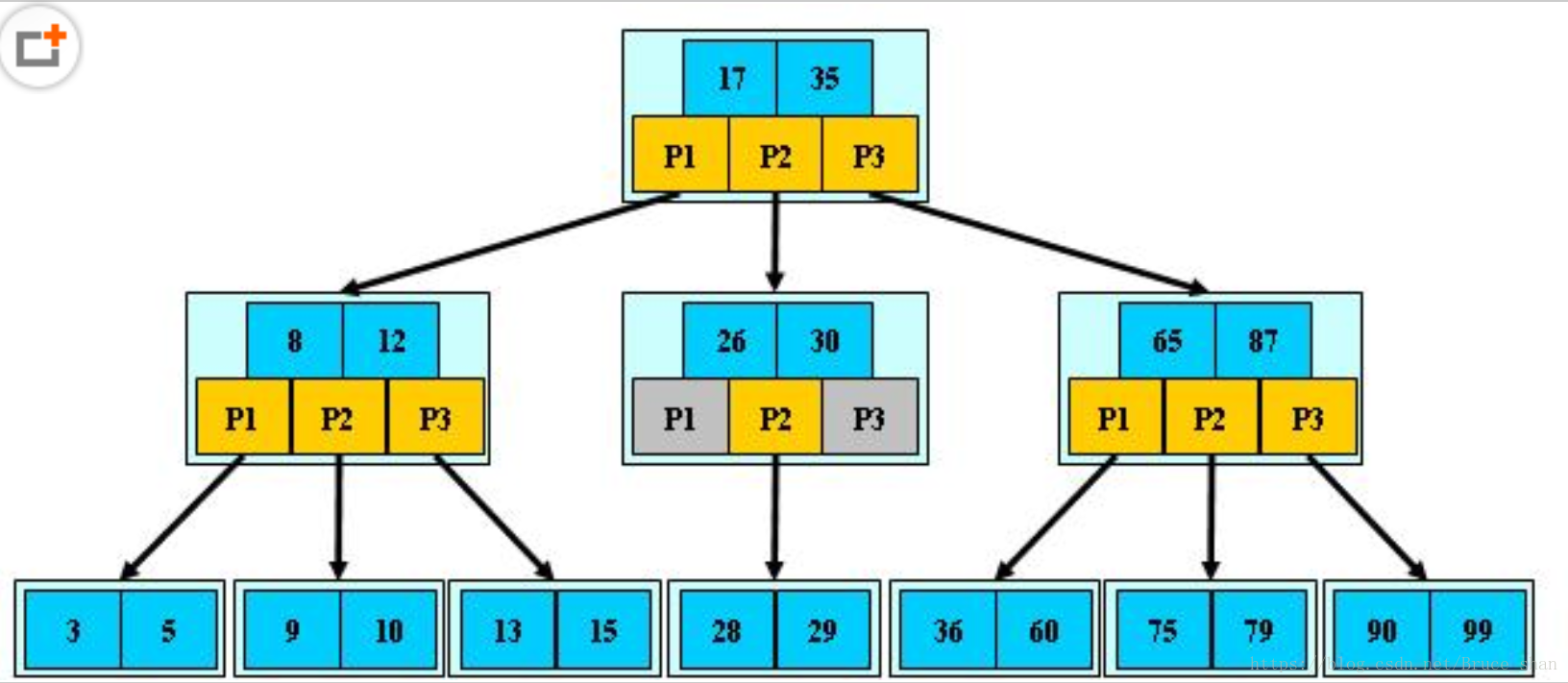
2.B-Tree的特點

1. 樹中每個結點最多含有m個孩子（m>=2）；
2. 除根結點和葉子結點外，其它每個結點至少有[ceil(m / 2)]個孩子（其中ceil(x)是一個取上限的函式）；
3. 若根結點不是葉子結點，則至少有2個孩子（特殊情況：沒有孩子的根結點，即根結點為葉子結點，整棵樹只有一個根節點）；
4. 所有葉子結點都出現在同一層(最底層)，葉子結點為外部結點，儲存內容，即key和value。
   
5. 其他結點為內部結點，儲存索引，即key和next。

上圖是一顆3階B樹

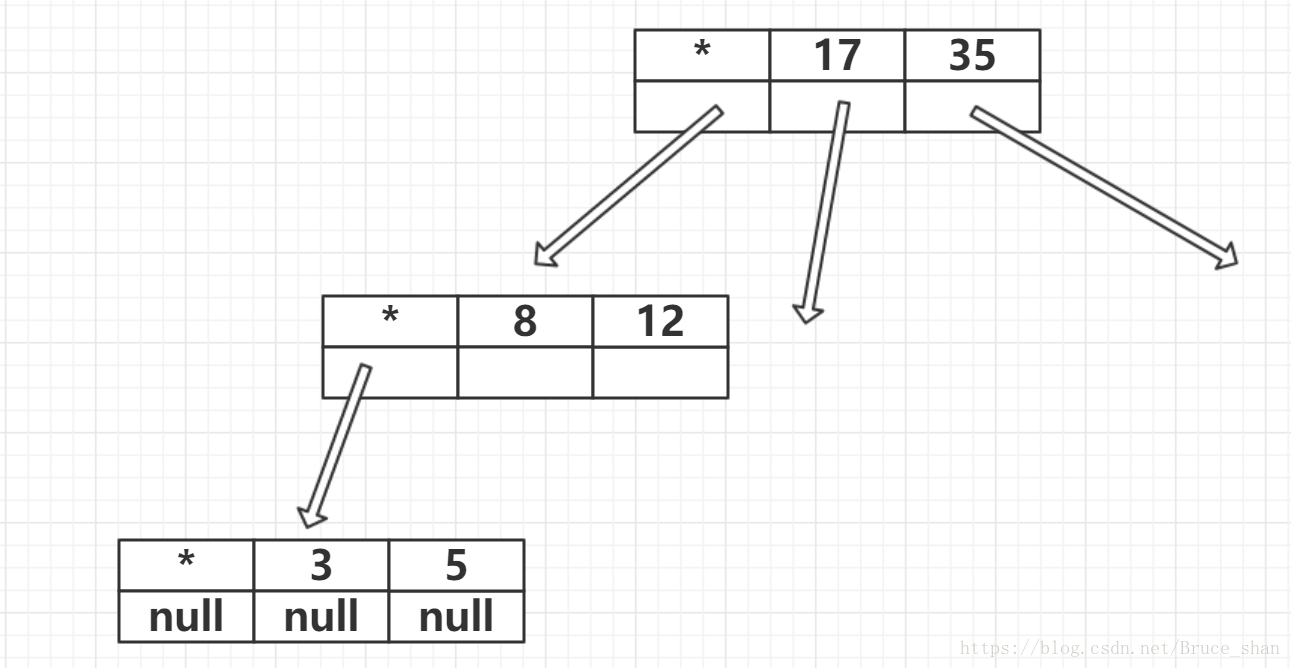
為了方便這裡用了一個特殊的哨兵鍵，它小於其他所有鍵，用*表示。

一開始B樹只含有一個根結點，而根結點在初始化時僅含有該哨兵鍵。

內部結點中的每個鍵都與一個結點相關聯，以此結點為根的子樹種，所有的鍵都大於等於與此結點關聯的鍵，但小於其他所有鍵。

這些約定在很大程度上能夠簡化程式碼。

Java 程式碼實現

package tree;


/**
 * Created by bruce_shan on 2018/7/8 17:08.
 * Description :  B-樹 也作 B樹  java 實現
 */
public class BTree<Key extends Comparable<Key>, Value> {

    private static final int M = 4;  // B樹的階數

    private Node root;       //  B-tree 的根節點
    private int height;      //  B-tree 的高度
    private int N;           //  B-tree 樹中鍵值對的數目

    // B-tree 節點型別
    private static final class Node {
        private int m;                             // number of children
        private Entry[] children = new Entry[M];   // the array of children
        // create a node with k children
        private Node(int k) {
            m = k;
        }
    }
    //  B-tree 節點中的元素型別
    private static class Entry {
        private Comparable key;
        private Object val;
        private Node next;     // 指向節點中下一元素
        public Entry(Comparable key, Object val, Node next) {
            this.key  = key;
            this.val  = val;
            this.next = next;
        }
    }


    /**
     * 初始化空 B-tree樹
     */
    public BTree() {
        root = new Node(0);
    }

    /**
     *  判斷 B-tree 是否是空樹
     */
    public boolean isEmpty() {
        return size() == 0;
    }

    public int size() {
        return N;
    }

    public int height() {
        return height;
    }

    /**
     *   get操作
     */
    public Value get(Key key) {
        if (key == null) throw new NullPointerException("key must not be null");
        return search(root, key, height);
    }

    /**
     *   put 操作
     */
    public void put(Key key, Value val) {
        if (key == null) throw new NullPointerException("key must not be null");
        Node u = insert(root, key, val, height);
        N++;
        if (u == null) return;

        // need to split root
        Node t = new Node(2);
        t.children[0] = new Entry(root.children[0].key, null, root);
        t.children[1] = new Entry(u.children[0].key, null, u);
        root = t;
        height++;
    }


    //  搜尋操作
    private Value search(Node x, Key key, int ht) {
        Entry[] children = x.children;

        // 節點內陣列操作  內部遍歷
        if (ht == 0) {
            for (int j = 0; j < x.m; j++) {
                if (equals(key, children[j].key)) return (Value) children[j].val;
            }
        }

        //  外部定位
        else {
            for (int j = 0; j < x.m; j++) {
                if (j+1 == x.m || less(key, children[j+1].key))
                    return search(children[j].next, key, ht-1);
            }
        }
        return null;
    }
    //  插入操作
    private Node insert(Node h, Key key, Value val, int ht) {
        int j;
        Entry t = new Entry(key, val, null);

        // 節點內部陣列操作
        if (ht == 0) {
            for (j = 0; j < h.m; j++) {
                if (less(key, h.children[j].key)) break;
            }
        }
        // 外部遍歷
        else {
            for (j = 0; j < h.m; j++) {
                if ((j+1 == h.m) || less(key, h.children[j+1].key)) {
                    Node u = insert(h.children[j++].next, key, val, ht-1);
                    if (u == null) return null;
                    t.key = u.children[0].key;
                    t.next = u;
                    break;
                }
            }
        }

        for (int i = h.m; i > j; i--)
            h.children[i] = h.children[i-1];
        h.children[j] = t;
        h.m++;
        if (h.m < M) return null;
        else         return split(h);
    }

    //  分裂節點成兩半
    private Node split(Node h) {
        Node t = new Node(M/2);
        h.m = M/2;
        for (int j = 0; j < M/2; j++)
            t.children[j] = h.children[M/2+j];
        return t;
    }
    // 判斷兩個元素是否相等
    private boolean equals(Comparable k1, Comparable k2) {
        return k1.compareTo(k2) == 0;
    }

    // 判斷兩個元素的大小
    private boolean less(Comparable k1, Comparable k2) {
        return k1.compareTo(k2) < 0;
    }
}