平衡二叉樹調整

平衡二叉樹簡稱平衡樹，是由Adelson-Velskii和Landis於1962年首先提出的，所以又稱為AVL樹。他的定義很簡單，就是若一棵二叉樹的每個左右節點的高度差最多相差1，此二叉樹即是平衡二叉樹。把二叉樹的每個節點的左子樹減去右子樹定義為該節點的平衡因子。二叉平衡樹的平衡因子只能是1、0或者-1。

平衡二叉樹是對二叉搜尋樹(又稱為二叉排序樹)的一種改進。二叉搜尋樹有一個缺點就是，樹的結構是無法預料的，隨意性很大，它只與節點的值和插入的順序有關係，往往得到的是一個不平衡的二叉樹。在最壞的情況下，可能得到的是一個單支二叉樹，其高度和節點數相同，相當於一個單鏈表，對其正常的時間複雜度有O(lb n)變成了O(n)，從而喪失了二叉排序樹的一些應該有的優點。

當插入一個新的節點的時候，在普通的二叉樹中不用考慮樹的平衡因子，只要將大於根節點的值插入到右子樹，小於節點的值插入到左子樹，遞迴即可。而在平衡二叉樹則不一樣，在插入節點的時候，如果插入節點之後有一個節點的平衡因子要大於2或者小於-2的時候，他需要對其進行調整，現在只考慮插入到節點的左子樹部分（右子樹與此相同）。主要分為以下三種情況：

(1)若插入前一部分節點的左子樹高度和右子樹高度相等，即平衡因子為0，插入後平衡因子變為1，仍符合平衡的條件不用調整。

(2)若插入前左子樹高度小於右子樹高度，即平衡因子為-1，則插入後將使平衡因子變為0，平衡性反倒得到調整，所以不必調整。

(3)若插入前左子樹的高度大於右子樹高度，即平衡因子為1，則插入左子樹之後會使得平衡因子變為2，這樣的情況下就破壞了平衡二叉樹的結構，所以必須對其進行調整，使其加以改善。

調整二叉樹首先要明白一個定義，即最小不平衡子樹。最小不平衡子樹是指以離插入節點最近、且平衡因子絕對值大於1的節點做根的子樹。

下面講解平衡二叉樹最基本的4種調整操作，調整的原則是調整後他的搜尋二叉樹的性質不變，即樹的中序遍歷是不會改變的：

1. LL型調整。在B點的左子樹上插入一個節點。插入後B點的左子樹的平衡因子變為1，A節點的平衡因子變為了2。這樣可以看出來A節點為根節點的子樹是最小不平衡子樹。調整時，將A的左孩子B向右旋轉代替A稱為原來不平衡子樹的根節點，將A的節點右下旋轉稱為B的右子樹的根節點，而B的原右子樹變為A的左子樹。詳細過程如下圖：

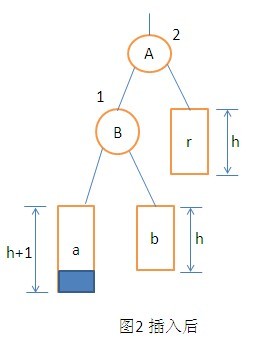
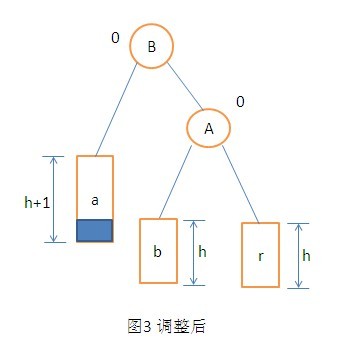
2. RR型調整操作

在A節點的右孩子的右子樹上插入節點，使得A節點的平衡因子由-1變為-2而引起的不平衡所進行的調整操作。調整操作大致一樣，看圖就可以明白了。

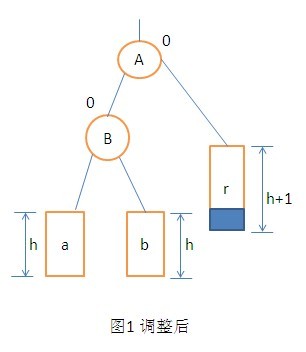
3. LR型的調整操作。在A節點的左孩子的右子樹上插入節點，使得A節點的平衡因子由1變為了2而引起的不平衡所進行的調整的操作。調整過程如圖：

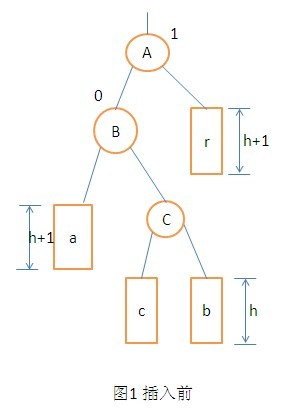
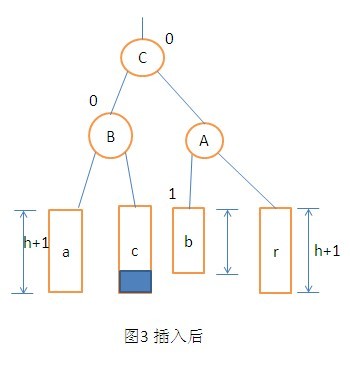
解釋：LR型先向左轉再向右旋轉。B先變為C的左子樹，CL變為B的右子樹；然後右旋的含義為A變成C的右子樹,CR變為A的左子樹。

4. RL型的調整操作。不多說了，直接上圖：

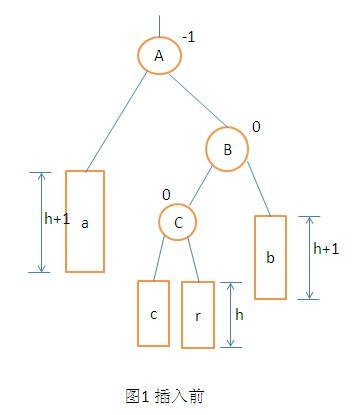
在二叉搜尋樹的插入和刪除運算中，採用平衡樹的優點是：使樹的結構較好，從而提高查詢運算的速度。缺點是：是插入和刪除運算變得複雜化，從而降低了他們的運算速度。對二叉搜尋樹刪除節點而引起的不平衡性進行的操作比插入節點的情況要複雜，在此就不再論述了。