後序線索化二叉樹及遍歷(圖解)
阿新 • • 發佈:2018-12-25
寫在前面
其實,我還是很想把本篇部落格和二叉樹的線索化寫在一塊的,但是考慮到可能這部落格的內容就看足以超過了上一篇的篇幅,考慮到讀者可能會疲乏,而且這篇也是線索二叉樹中最難的了(查閱了很多網上的資料也鮮有人來講述後序線索二叉樹的遍歷,有的就算有也只是把程式碼放在那裡,理解 對於初學者還是有點困難的)
構建節點(多了雙親節點節點)
typedef enum { Link, Thread }Pointer; typedef struct TriTreeNode { TriTreeNode(const char data) :_data(data) , pLeft(NULL) , pRight(NULL) , pParent(NULL) , Ltag(Link) , Rtag(Link) {} char _data; struct TriTreeNode* pLeft; struct TriTreeNode* pRight; struct TriTreeNode* pParent;//雙親 Pointer Ltag, Rtag; }TriTreeNode;
還是先給出一個樹結構吧:
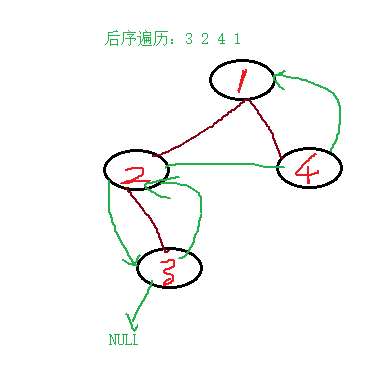
後序線索化二叉樹
後序的順序是:左- 右-根
思路:和先序、中序線索化二叉樹的順序是一樣的,在此不再贅述,想看的話上一篇部落格會讓你滿意的。
上程式碼:
void _PostThreading(TriTreeNode*& Root) { if (Root) { _PostThreading(Root->pLeft); _PostThreading(Root->pRight); if (Root->pLeft == NULL) { Root->pLeft = Prev; Root->Ltag = Thread; } if (Prev && Prev->pRight == NULL ) //條件 Prev { Prev->pRight = Root; Prev->Rtag = Thread; } Prev = Root; } }
如下圖,後序線索化的二叉樹
!!!
後序遍歷線索二叉樹
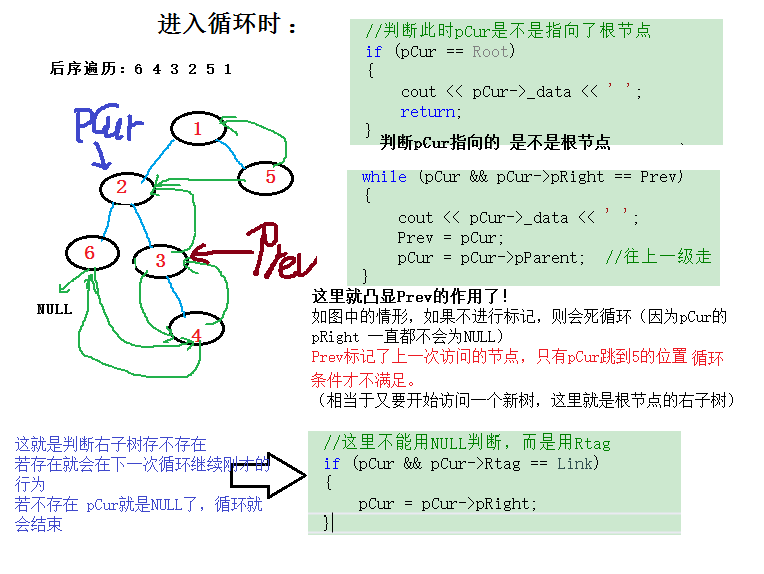
由後序遍歷的順序,我們很容易就想到了找到後序遍歷的起點(左子樹最左邊的節點),然後一直遍歷節點的後繼(記住每次遍歷的前一個節點),當遍歷到節點沒有後繼了,我們就判斷是不是到了根節點了(如果根節點沒有右子樹,就是這種情況了),要是還沒有到根節點,那就繼續找尋節點的雙親節點(此時就需要我們催節點的結構進行增加雙親節點了),一直找到根節點的位置,繼續判斷根節點是不是存在右子樹(注意這裡不能用NULL判斷右子樹是不是存在,而是用右子樹存在的標識Rtag )
好了,描述再多還是程式碼程式碼來的實在!!!
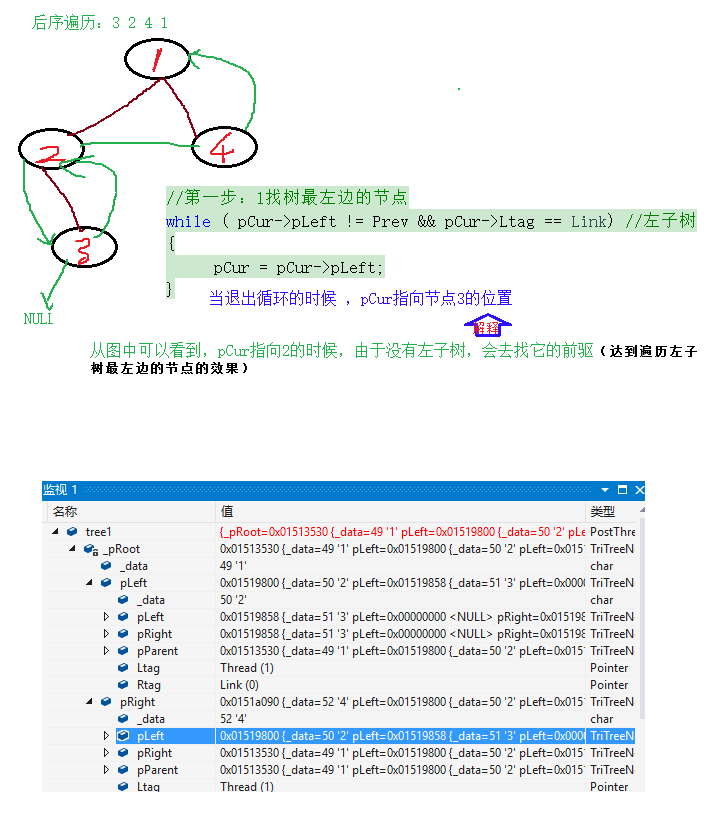
下面就是對程式碼的一一講述 <福利來了>void _PostOrder(TriTreeNode* Root) { if (Root) { TriTreeNode* pCur = Root; Prev = NULL; while (pCur != NULL) { //第一步:找樹最左邊的節點 while ( pCur->pLeft != Prev && pCur->Ltag == Link) //左子樹 { pCur = pCur->pLeft; } //迴圈結束後 pCur== Root 或者為空 //第二步:訪問後繼 while (pCur && pCur->Rtag== Thread) { cout << pCur->_data << ' '; Prev = pCur; pCur = pCur->pRight; } //判斷此時pCur是不是指向了根節點 if (pCur == Root) { cout << pCur->_data << ' '; return; } while (pCur && pCur->pRight == Prev) { cout << pCur->_data << ' '; Prev = pCur; pCur = pCur->pParent; //往上一級走 } //這裡不能用NULL判斷,而是用Rtag if (pCur && pCur->Rtag == Link) { pCur = pCur->pRight; } } //end-while } }
首先對,大迴圈中的第一個迴圈解釋(找到最左邊的節點)
第二個迴圈(訪問後繼)
第三個迴圈以及後面的判斷
後面就是對程式碼的測試了
來個簡單的Tree
加深一點
再難點吧。哈哈
能看到這裡的都是好樣的!
全部程式碼:
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
typedef enum
{
Link,
Thread
}Pointer;
typedef struct TriTreeNode
{
TriTreeNode(const char data)
:_data(data)
, pLeft(NULL)
, pRight(NULL)
, pParent(NULL)
, Ltag(Link)
, Rtag(Link)
{}
char _data;
struct TriTreeNode* pLeft;
struct TriTreeNode* pRight;
struct TriTreeNode* pParent;//雙親
Pointer Ltag, Rtag;
}TriTreeNode;
class PostThread_BiTree
{
public://先序遍歷建立樹
PostThread_BiTree(const char arr[], size_t size)
{
size_t index = 0;
TriTreeNode* parent = NULL;
_Creat_Bitree(_pRoot, arr, size, index, parent);
}
protected:
void _Creat_Bitree(TriTreeNode*& Root, const char arr[], size_t size, size_t& index , TriTreeNode*& parent)
{
if (arr && size > index && arr[index] != '#')
{
Root = new TriTreeNode(arr[index]);
Root->pParent = parent;
_Creat_Bitree(Root->pLeft, arr, size, ++index , Root); //每次傳雙親節點
_Creat_Bitree(Root->pRight, arr, size, ++index , Root);
}
}
public:
//後序線索化
void PostTreading()
{
_PostThreading(this->_pRoot);
}
protected:
void _PostThreading(TriTreeNode*& Root)
{
if (Root)
{
_PostThreading(Root->pLeft);
_PostThreading(Root->pRight);
if (Root->pLeft == NULL)
{
Root->pLeft = Prev;
Root->Ltag = Thread;
}
if (Prev && Prev->pRight == NULL ) //條件 Prev
{
Prev->pRight = Root;
Prev->Rtag = Thread;
}
Prev = Root;
}
}
public:
void PostOrder()
{
_PostOrder(this->_pRoot);
}
protected:
void _PostOrder(TriTreeNode* Root)
{
if (Root)
{
TriTreeNode* pCur = Root;
Prev = NULL;
while (pCur != NULL)
{
//第一步:找樹最左邊的節點
while ( pCur->pLeft != Prev && pCur->Ltag == Link) //左子樹
{
pCur = pCur->pLeft;
}
//迴圈結束後 pCur== Root 或者為空
//第二步:訪問後繼
while (pCur && pCur->Rtag== Thread)
{
cout << pCur->_data << ' ';
Prev = pCur;
pCur = pCur->pRight;
}
//判斷此時pCur是不是指向了根節點
if (pCur == Root)
{
cout << pCur->_data << ' ';
return;
}
while (pCur && pCur->pRight == Prev)
{
cout << pCur->_data << ' ';
Prev = pCur;
pCur = pCur->pParent; //往上一級走
}
//這裡不能用NULL判斷,而是用Rtag
if (pCur && pCur->Rtag == Link)
{
pCur = pCur->pRight;
}
}
//end-while
}
}
private:
TriTreeNode* _pRoot;
TriTreeNode* Prev;
};
void Test()
{
char* arr = "013##4##25##6##";
PostThread_BiTree tree(arr, strlen(arr)); //構建三叉樹
tree.PostTreading();
tree.PostOrder();//arr 3 4 1 5 6 2 0
cout << endl << "______________________" << endl;
char* arr1 = "013##4##2#56###";
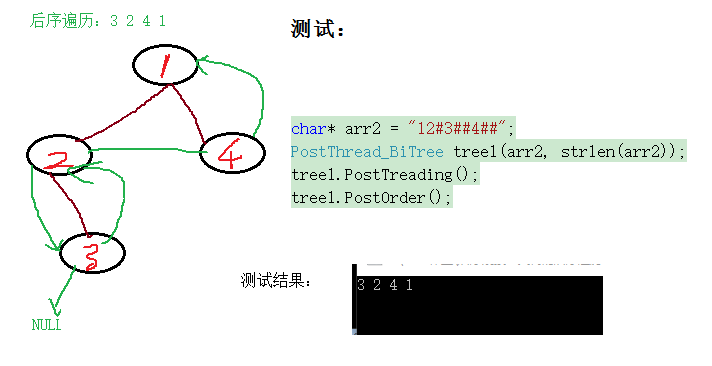
char* arr2 = "12#3##4##";
PostThread_BiTree tree1(arr2, strlen(arr2));
tree1.PostTreading();
tree1.PostOrder();
cout << endl << "______________________" << endl;
char* arr3 = "12#3#4##5##";
PostThread_BiTree tree2(arr3, strlen(arr3));
tree2.PostTreading();
tree2.PostOrder();
cout << endl << "______________________" << endl;
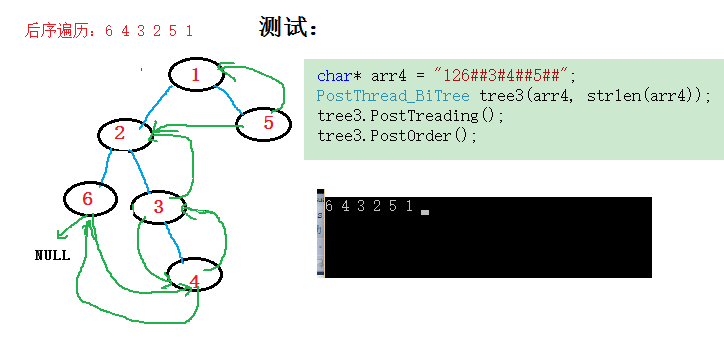
char* arr4 = "126##3#4##5##";
PostThread_BiTree tree3(arr4, strlen(arr4));
tree3.PostTreading();
tree3.PostOrder();
cout << endl << "______________________" << endl;
}
int main()
{
Test();
return 0;
}