2. 程式人生 > >資料結構--樹--線索二叉樹（中序，前序，後序）

資料結構--樹--線索二叉樹（中序，前序，後序）

阿新 • • 發佈：2018-12-25

線索二叉樹

在遍歷二叉樹的時候，會有許多空指標域，這些空間不儲存任何事物，白白浪費了記憶體的資源。
那麼在做遍歷的時候，提前記錄下每個結點的前驅和後繼，這樣就更加節約了時間。
                 [ lchild ] [ LTag ] [ data ] [ RTag ] [ rchild ] 
LTag  = { 0 : lchild 域指示結點的左孩子 1 : lchild 域指示結點的前驅 } 
RTag = { 0 : rchild 域指示結點的右孩子 1 : rchild 域指示結點的後繼 }  
以這種結點結構構成的二叉連結串列作為二叉樹的儲存結構，叫做線索連結串列，其中，指向結點前驅和後繼的指標，叫做線索
。
加上線索的二叉樹叫做線索二叉樹（Threaded Binary Tree）
對二叉樹以某種次序遍歷使其變成線索二叉樹的過程叫做線索化


★線索二叉樹結構：
#define TElemType char
typedef enum{
	Link,Thread
}PointerTag;//Link == 0 :指標 ,Thread == 1: 線索 
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode *lchild, *rchild; //左右孩子指標
	PointerTag LTag , RTag;            //左右標誌 
}BiThrNode, *BiThrTree;

                 [ lchild ] [ LTag ] [ data ] [ RTag ] [ rchild ] 
LTag  = { 0 : lchild 域指示結點的左孩子 1 : lchild 域指示結點的前驅 } 
RTag = { 0 : rchild 域指示結點的右孩子 1 : rchild 域指示結點的後繼 }  


★線索化二叉樹之前，咱們先把樹建起來（用前序遍歷建樹）
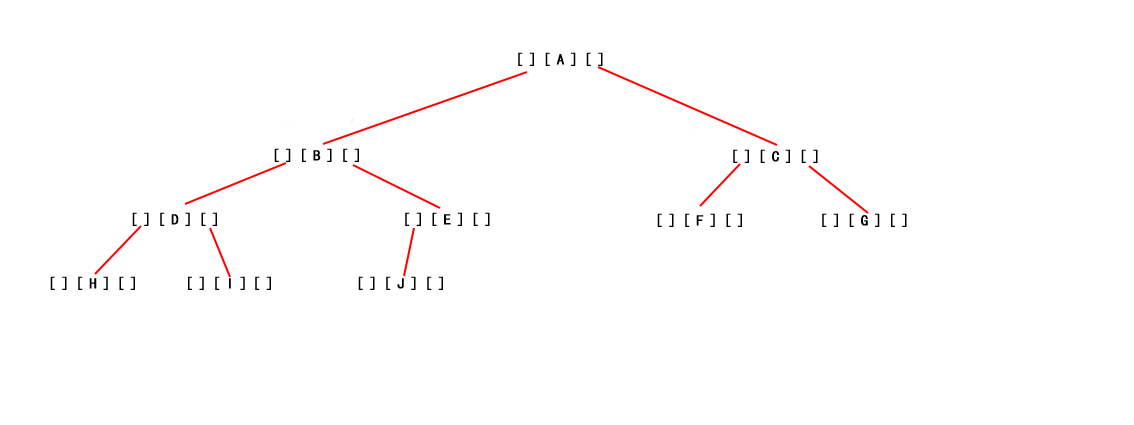
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};  
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};  
int i=0;  
//二叉樹的建立  
Status CreatBiThrTree(BiThrTree &T)  
{  
    if(Vexch[i++]=='$') T=NULL;  
    else  
    {  
        T= (BiThrTree)malloc(sizeof(BiThrNode)); 
        if(!T)  return 0;  
        T->data=Vexch[i-1];//生成根節點  
        printf("%5c",T->data);
        T->LTag=Link;  
        CreatBiThrTree(T->lchild);//建立左子樹 
		T->RTag=Link; 
        CreatBiThrTree(T->rchild);//建立右子樹  
    }  
    return 1;  
}

建立樹為該樹：
 

遍歷visit()函式
Status visit(TElemType e){
	printf("%5c",e);
	return OK;
}

（1）中序遍歷，線索二叉樹

【讓一棵樹 直接變成一個線性表去遍歷】
遍歷 順序為：H - >D - > I - > B  - > J - > E - > A - > F - > C - >  G
【建立二叉樹頭結點】（下面的程式碼沒有迴圈，只是單純的建立了一個頭結點，連線上主體的樹部分，方便遍歷。）
//建立頭結點，中序線索二叉樹 
Status InOrderThreading(BiThrTree &Thrt,BiThrTree T){
	//中序遍歷二叉樹T，並將其中序線索化，Thrt指向頭結點。
	if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) 
		return ERROR;
	 
	Thrt->RTag = Link;  //建頭結點
	Thrt->rchild = Thrt ;                    //右指標回指 
	if(!T){
		Thrt->lchild = Thrt;
		Thrt->LTag = Link;
	}else{
		pre = Thrt ;
		Thrt->lchild = T; 
		Thrt->LTag = Link;
		InThreading(T); 
		pre->rchild = Thrt ; 
		pre->RTag = Thread; 
		Thrt->rchild = pre;
	}
	return OK;
}
【解釋】（pre永遠指向上一個節點）
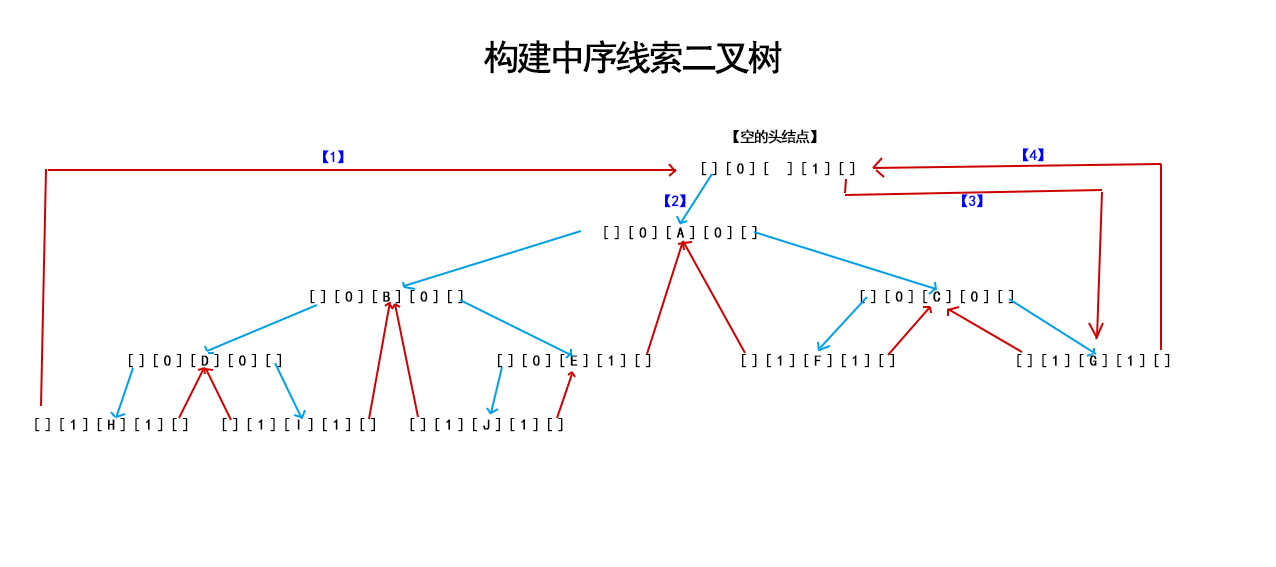
Thrt 就是 下圖的空指標， 初始化 pre 為 這個空指標，完成下圖的【1】【2】步驟
做完樹的線索化後，pre 已經到了最後一個節點，那麼就可以完成【3】【4】兩個步驟了
如下圖所示。
【1】讓最左的結點，就是中序遍歷時 第一個結點的左指標指向 空的頭結點。
【第一個結點的左標記肯定是 Thread而不是 link ，這樣就能找到最左的結點】 那麼既然是線索Thread，就讓他指向空的頭結點（反正空著也是空著）
【2】頭結點順下來，從左子樹開始找
【3】因為空節點的右標記是 Thread線索，那麼讓他指向最右的，最終結點。（反正空著也是空著）
【4】最終結點G的右線索指向頭結點，標記著終結。
構成迴圈：
                    ↓   →  →  →  →   【  空的頭結點】 ← ←  ←  ← ↑
                   H → D →  I → B  →  J → E →  A → F →  C →  G
 

★LTag  = { 0 : lchild 域指示結點的左孩子 1 : lchild 域指示結點的前驅 } RTag = { 0 : rchild 域指示結點的右孩子 1 : rchild 域指示結點的後繼 }  
概括為：LTag=0(Link)【左孩子】，LTag=1(Thread)【前驅】；RTag=0(Link)【右孩子】 ，RTag=1(Thread)【後繼】
【問】那麼怎樣的稱為Link指標 ，怎樣的 稱為 Thread 線索

【答】可以這樣理解，Link指標是本來建樹的時候就有的，而Thread線索是為了線索化，而增添的。

【中序遍歷線索化】
BiThrTree pre;  //全域性變數，始終指向剛剛訪問過的結點。 
void InThreading(BiThrTree p){
	if(p){
		InThreading(p->lchild);     //左子樹線索化
		if(!p->lchild){             //沒有左孩子 
			p->LTag = Thread;       //前驅線索 
			p->lchild = pre;        //左孩子指標指向前驅 
		}
		if(!pre->rchild){
			pre->RTag = Thread;       //後繼線索
			pre->rchild = p ;         //前驅右孩子指標指向後繼 
		}
		pre = p;
		InThreading(p->rchild);   //右子樹線索化 
	}
}
【解釋】
首先，很明顯：中序遍歷線索化，其實也是基於中序遍歷的。（從程式碼中可以看出）
也是先左，再中，後右（左 > 中 > 右）
只是在中間部分，對結點的處理的時候，有些不一樣。1、中序遍歷時是輸出。2、而現在我們把它替換為 處理標記和指標。
介紹如何處理，很簡單：
★沒有左孩子，或者沒有右孩子那肯定是線索，而不是指標
★因為是中序，遍歷肯定是從左到右，那麼左邊的線索肯定是指向前驅的，右邊的線索肯定是指向後繼的。


【中序遍歷】
//中序 遍歷線索二叉樹 
Status InOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
	//T指向頭結點，頭結點的左鏈lchild指向根節點，可參見線索化演算法
	//中序遍歷二叉線索樹T的非遞迴演算法，對每個資料元素呼叫函式visit
	BiThrTree p ;
	p = T->lchild;            // p指向根節點 
	while(p != T){                      //空樹 或者遍歷結束時 p == T
		while(p->LTag == Link )         // 走到最左結點 
			p = p->lchild;
		visit(p->data);  
		while(p->RTag == Thread && p->rchild !=T){
			p = p->rchild ;             // 若有右線索， 
			visit(p->data);
		}
		p = p->rchild;
	}
	return OK;
}
【解釋】
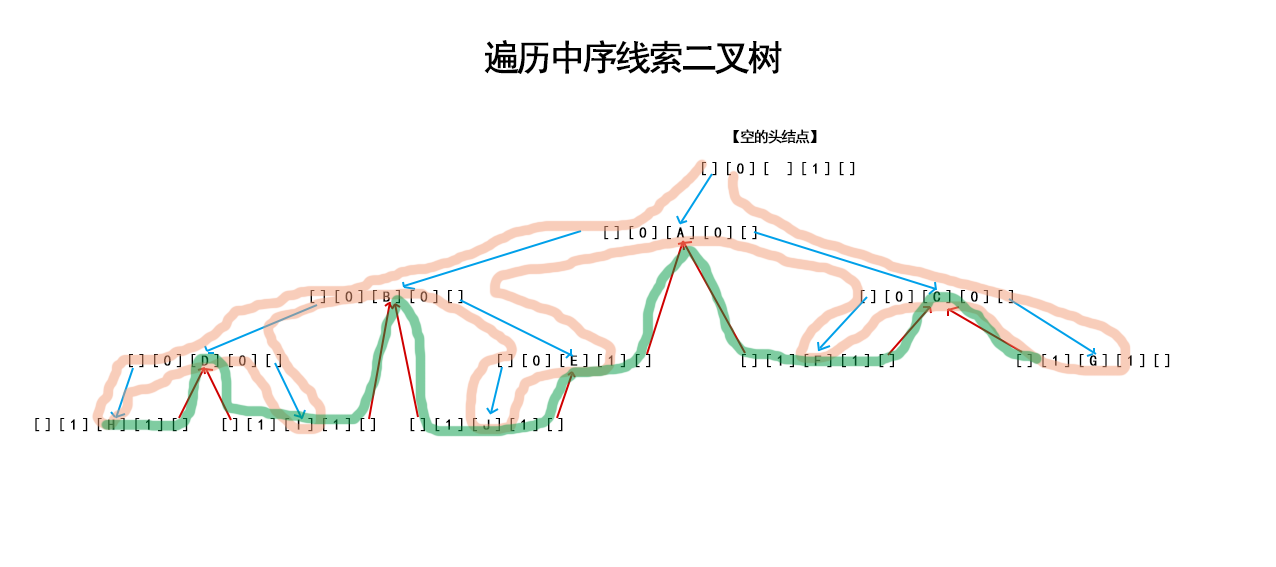
最外面的while 從上面構造的時候就已經說明了，當p回到T的時候，那麼就標記結束了。
裡面的第一個 while(p->LTag == Link) 迴圈，走到最左結點
輸出該節點
while(p->RTag == Thread && p->rchild !=T)  如果右邊有線索，且指向的不是最後的根T， 優先按著線索走。
發現這裡沒有線索了，那麼就繼續往右孩子找。


【總的中序遍歷線索二叉樹程式碼】
#include <iostream>
#include <string.h>
#include <cstdio>
#include <stdlib.h>
using namespace std;
#define Status int 
#define OK 1
#define ERROR 0
#define TElemType char
typedef enum{
	Link,Thread
}PointerTag;//Link == 0 :指標 ,Thread == 1: 線索 
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode *lchild, *rchild; //左右孩子指標
	PointerTag LTag , RTag;            //左右標誌 
}BiThrNode, *BiThrTree;

//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};  
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};  
int i=0;  
//二叉樹的建立  
Status CreatBiThrTree(BiThrTree &T)  
{  
    if(Vexch[i++]=='$') T=NULL;  
    else  
    {  
        T= (BiThrTree)malloc(sizeof(BiThrNode)); 
        if(!T)  return 0;  
        T->data=Vexch[i-1];//生成根節點  
        printf("%5c",T->data);
        T->LTag=Link;  
        CreatBiThrTree(T->lchild);//建立左子樹 
		T->RTag=Link; 
        CreatBiThrTree(T->rchild);//建立右子樹  
    }  
    return 1;  
}  
Status visit(TElemType e){
	printf("%5c",e);
	return OK;
}

BiThrTree pre;  //全域性變數，始終指向剛剛訪問過的結點。 
void InThreading(BiThrTree p){
	if(p){
		InThreading(p->lchild);     //左子樹線索化
		if(!p->lchild){             //沒有左孩子 
			p->LTag = Thread;       //前驅線索 
			p->lchild = pre;        //左孩子指標指向前驅 
		}
		if(!pre->rchild){
			pre->RTag = Thread;       //後繼線索
			pre->rchild = p ;         //前驅右孩子指標指向後繼 
		}
		pre = p;
		InThreading(p->rchild);   //右子樹線索化 
	}
}
//建立頭結點，中序線索二叉樹 
Status InOrderThreading(BiThrTree &Thrt,BiThrTree T){
	//中序遍歷二叉樹T，並將其中序線索化，Thrt指向頭結點。
	if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) 
		return ERROR;
	 
	Thrt->RTag = Link;  //建頭結點
	Thrt->rchild = Thrt ;                    //右指標回指 
	if(!T){
		Thrt->lchild = Thrt;
		Thrt->LTag = Link;
	}else{
		pre = Thrt ;
		Thrt->lchild = T; 
		Thrt->LTag = Link;
		InThreading(T); 
		pre->rchild = Thrt ; 
		pre->RTag = Thread; 
		Thrt->rchild = pre;
	}
	return OK;
}
//中序 遍歷線索二叉樹 
Status InOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
	//T指向頭結點，頭結點的左鏈lchild指向根節點，可參見線索化演算法
	//中序遍歷二叉線索樹T的非遞迴演算法，對每個資料元素呼叫函式visit
	BiThrTree p ;
	p = T->lchild;            // p指向根節點 
	while(p != T){                      //空樹 或者遍歷結束時 p == T
		while(p->LTag == Link )         // 走到最左結點 
			p = p->lchild;
		visit(p->data);  
		while(p->RTag == Thread && p->rchild !=T){
			p = p->rchild ;             // 若有右線索， 
			visit(p->data);
		}
		p = p->rchild;
	}
	return OK;
}
int main()
{
	BiThrTree T, inorderT;
	printf("建立樹\n");
	CreatBiThrTree(T);
	printf("\n中序遍歷線索二叉樹\n");
	InOrderThreading(inorderT , T);
	InOrderTraverse_Thr(inorderT , visit);
	printf("\n");
	return 0;
}



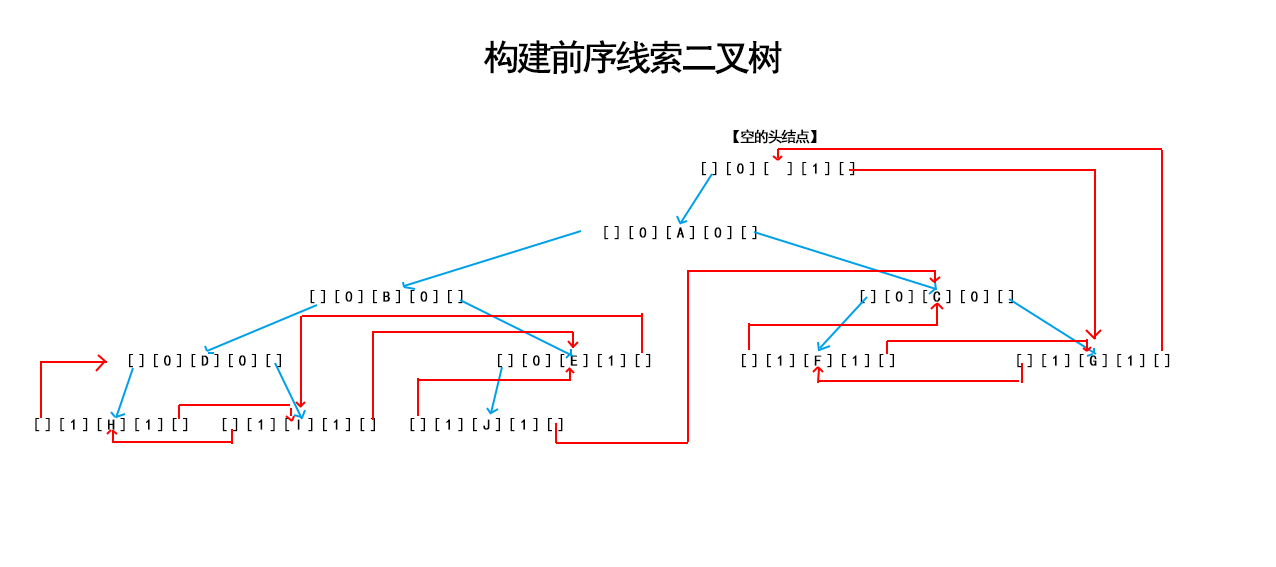
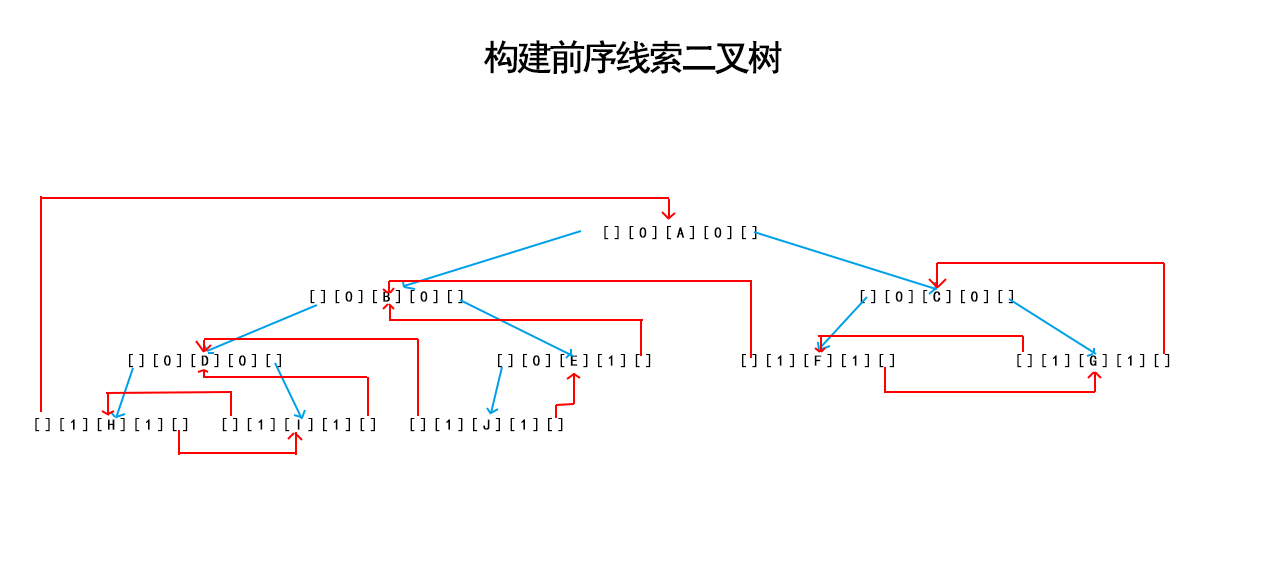
（2）前序遍歷，線索二叉樹

【前序遍歷二叉樹線索化】

BiThrTree pre;  //全域性變數，始終指向剛剛訪問過的結點。 
void PreThreading(BiThrTree p){
	if(p){
		if(!p->lchild){             //沒有左孩子 
			p->LTag = Thread;       //前驅線索 
			p->lchild = pre;        //左孩子指標指向前驅 
		}
		if(!pre->rchild && pre){
			pre->RTag = Thread;       //後繼線索
			pre->rchild = p ;         //前驅右孩子指標指向後繼 
		}
		pre = p;
		if(p->LTag == Link)
			PreThreading(p->lchild);     //左子樹線索化
		if(p->RTag == Link)
			PreThreading(p->rchild);   //右子樹線索化 
	}
}
【建立頭結點】（和中序遍歷一樣）
//建立頭結點，前序線索二叉樹 
Status PreOrderThreading(BiThrTree &Thrt,BiThrTree T){
	//前序遍歷二叉樹T，並將其前序線索化，Thrt指向頭結點。
	if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) 
		return ERROR;
	
	Thrt->RTag = Thread;               //建頭結點
	Thrt->rchild = Thrt ;              //右指標回指 
	Thrt->LTag = Link;
	if(!T){
		Thrt->lchild = Thrt;
	}else{
		Thrt->lchild = T; 
		pre = Thrt ;
		PreThreading(T); 
		pre->rchild = Thrt ; 
		pre->RTag = Thread; 
		Thrt->rchild = pre;
	}
	return OK;
}

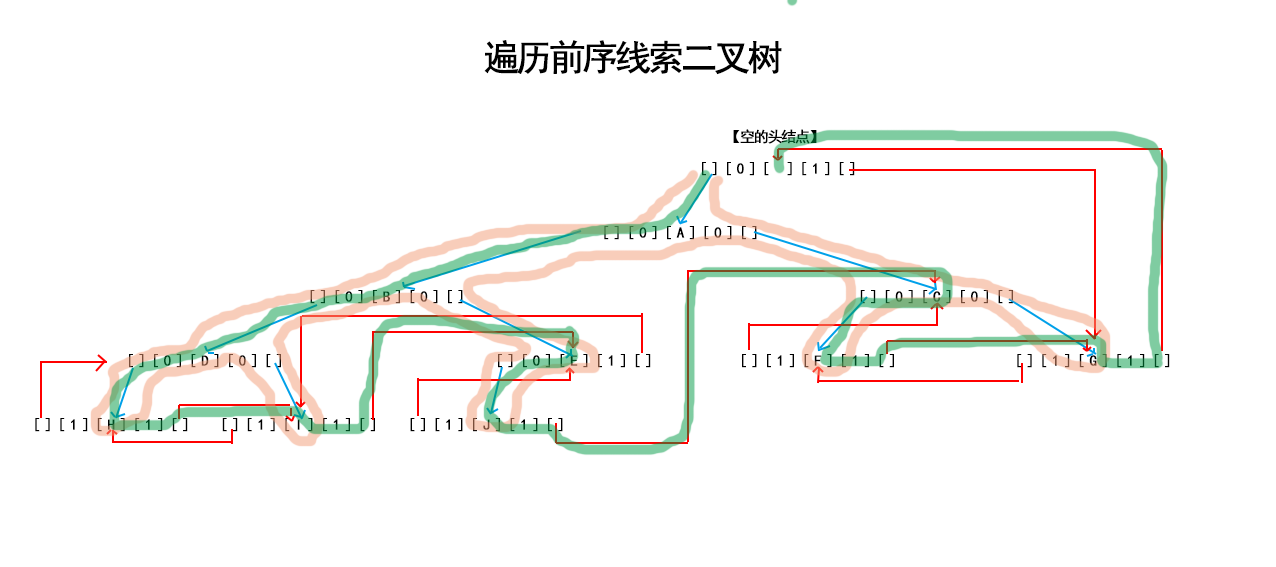
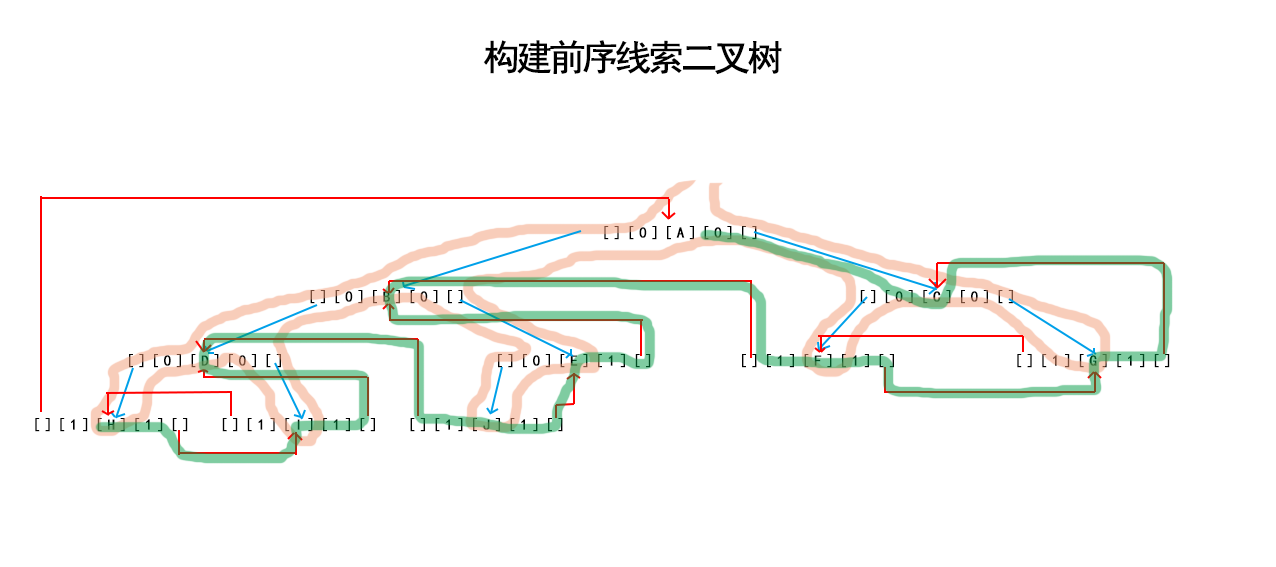
                                                                               ↓  ← 【  空的頭結點  】 ← ←  ←  ←  ←  ←  ←   ↑
                                                                               A → B →  D → H  →  I →  E →  J → C →  F →  G


   

         1、A的直接前驅

          ㈠若LTag 的值為1，那麼LChild 所指結點就是直接前驅

          ㈡若LTag 的值為0，那麼

                 ⒈若A為雙親左兒子，那麼直接前驅就是A的雙親結點

                 ⒉若A為雙親右兒子，那麼直接前驅就是A的雙親左兒子

         2、A的直接後繼

          ㈠若RTag 的值為1，那麼RChild 所指結點就是直接後繼

          ㈡若RTag 的值為0，那麼

                  ⒈若LTag 的值為0，那麼直接後繼就是其左兒子。

                  ⒉若LTag 的值為1，那麼直接後繼就是其右兒子。


【前序遍歷二叉樹】
//前序 遍歷線索二叉樹 
Status PreOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
	//T指向頭結點，頭結點的左鏈lchild指向根節點，可參見線索化演算法
	//前序遍歷二叉線索樹T的非遞迴演算法，對每個資料元素呼叫函式visit
	BiThrTree p ;
	p = T->lchild;            // p指向根節點 
	while(p != T){            //空樹 或者遍歷結束時 p == T
		visit(p->data);  
		if(p->LTag == Link)
			p = p->lchild;
		else 
			p = p->rchild;
	}
	return OK;
}


【總的前序遍歷線索二叉樹程式碼】

#include <iostream>
#include <string.h>
#include <cstdio>
#include <stdlib.h>
using namespace std;
#define Status int 
#define OK 1
#define ERROR 0
#define TElemType char

typedef enum{
	Link,Thread
}PointerTag;//Link == 0 :指標 ,Thread == 1: 線索 
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode *lchild, *rchild; //左右孩子指標
	PointerTag LTag , RTag;            //左右標誌 
}BiThrNode, *BiThrTree;

//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};  
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};  
int i=0;  
//二叉樹的建立  
Status CreatBiThrTree(BiThrTree &T)  
{  
    if(Vexch[i++]=='$') T=NULL;  
    else  
    {  
        T= (BiThrTree)malloc(sizeof(BiThrNode)); 
        if(!T)  return 0;  
        T->data=Vexch[i-1];//生成根節點  
        printf("%5c",T->data);
		T->LTag=Link; 
        CreatBiThrTree(T->lchild);//建立左子樹 
		T->RTag=Link; 
        CreatBiThrTree(T->rchild);//建立右子樹  
    }  
    return 1;  
}  
Status visit(TElemType e){
	printf("%5c",e);
	return OK;
}

BiThrTree pre;  //全域性變數，始終指向剛剛訪問過的結點。 
void PreThreading(BiThrTree p){
	if(p){
		if(!p->lchild){             //沒有左孩子 
			p->LTag = Thread;       //前驅線索 
			p->lchild = pre;        //左孩子指標指向前驅 
		}
		if(!pre->rchild){
			pre->RTag = Thread;       //後繼線索
			pre->rchild = p ;         //前驅右孩子指標指向後繼 
		}
		pre = p;
		if(p->LTag == Link)
			PreThreading(p->lchild);     //左子樹線索化
		if(p->RTag == Link)
			PreThreading(p->rchild);   //右子樹線索化 
	}
}
//建立頭結點，前序線索二叉樹 
Status PreOrderThreading(BiThrTree &Thrt,BiThrTree T){
	//前序遍歷二叉樹T，並將其前序線索化，Thrt指向頭結點。
	if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) 
		return ERROR;
	
	Thrt->RTag = Thread;               //建頭結點
	Thrt->rchild = Thrt ;              //右指標回指 
	Thrt->LTag = Link;
	if(!T){
		Thrt->lchild = Thrt;
	}else{
		Thrt->lchild = T; 
		pre = Thrt ;
		PreThreading(T); 
		pre->rchild = Thrt ; 
		pre->RTag = Thread; 
		Thrt->rchild = pre;
	}
	return OK;
}
//前序 遍歷線索二叉樹 
Status PreOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
	//T指向頭結點，頭結點的左鏈lchild指向根節點，可參見線索化演算法
	//前序遍歷二叉線索樹T的非遞迴演算法，對每個資料元素呼叫函式visit
	BiThrTree p ;
	p = T->lchild;            // p指向根節點 
	while(p != T){            //空樹 或者遍歷結束時 p == T
		visit(p->data);  
		if(p->LTag == Link)
			p = p->lchild;
		else 
			p = p->rchild;
	}
	return OK;
}
int main()
{
	BiThrTree T, PreT;
	printf("建立樹\n");
	CreatBiThrTree(T);
	printf("\n前序遍歷線索二叉樹\n");
	PreOrderThreading(PreT , T);
	PreOrderTraverse_Thr(PreT , visit);
	printf("\n");
	return 0;
}

（3）後序遍歷，線索二叉樹

【後序遍歷線索二叉樹時，需要一個parent 指標，所以建樹的時候與上面兩個有所不同】

#define TElemType char
typedef enum{
	Link,Thread
}PointerTag;//Link == 0 :指標 ,Thread == 1: 線索 
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode *lchild, *rchild; //左右孩子指標
	struct BiThrNode *parent;
	PointerTag LTag , RTag;            //左右標誌 
}BiThrNode, *BiThrTree;
BiThrTree pre;  //全域性變數，始終指向剛剛訪問過的結點。

Status visit(TElemType e){
	printf("%5c",e);
	return OK;
}
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};  
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};  
int i=0;  
//二叉樹的建立  
Status CreatBiThrTree(BiThrTree &T,BiThrTree &p)  
{  
    if(Vexch[i++]=='$') T=NULL;  
    else  
    {  
        T= (BiThrTree)malloc(sizeof(BiThrNode)); 
        if(!T)  return 0;  
        T->data=Vexch[i-1];//生成根節點  
	T->parent = p;//指回原來的結點
        visit(T->data);
		T->LTag=Link; 
        CreatBiThrTree(T->lchild,T);//建立左子樹 
		T->RTag=Link; 
        CreatBiThrTree(T->rchild,T);//建立右子樹  
    }  
    return 1;  
}

【後序遍歷二叉樹線索化】
void PostThreading(BiThrTree p){
	if(p){
		PostThreading(p->lchild);     //左子樹線索化
		PostThreading(p->rchild);     //右子樹線索化 
		if(!p->lchild){               //沒有左孩子 
			p->LTag = Thread;         //前驅線索 
			p->lchild = pre;          //左孩子指標指向前驅 
		}
		if(pre && !pre->rchild){
			pre->RTag = Thread;       //後繼線索
			pre->rchild = p ;         //前驅右孩子指標指向後繼 
		}
		pre = p;
	}
}

【建立頭結點】（這裡就不建頭結點了，因為入口是總根節點，出口也是總根節點）


         1、A的直接前驅

          ㈠若LTag 的值為1，那麼A的直接前驅為LChild所指結點

          ㈡若LTag 的值為0，那麼

                  ⒈若有左兒子，那麼直接前驅就是A的左兒子。

                  ⒉若有右兒子，那麼直接前驅就是A的右兒子。

         2、A的直接後繼

          ㈠若結點A是二叉樹的根，則其後繼為空

          ㈡若結點A是其雙親的右兒子，或是雙親的左孩子且其雙親沒有左子樹沒有右子樹，則其後繼即為雙親結點

          ㈢若結點A是其雙親的左兒子，且雙親有右子樹，則其後繼為雙親的右子樹上按後序遍歷列出來的第一個結點。



【後序遍歷二叉樹】
//後序 遍歷線索二叉樹 
Status PostOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
	BiThrTree p ;
	p = T;            // p指向根節點 
	pre=NULL;
	while(p != NULL){            //空樹 或者遍歷結束時 p == T
		while(p->LTag == Link )         // 走到最左結點  ||左結點
			p = p->lchild;
		 
		while(p->RTag == Thread ){      //訪問後繼       ||右結點
			visit(p->data);
			pre = p;
			p = p->rchild ;            
		}
		if(p == T){                     //是否是最後根節點
			visit(p->data); 
			break;
		}
		while(p && p->rchild == pre  ){ //訪問根         ||根節點
			visit(p->data);
			pre = p;
			p = p->parent;
		}
		if(p && p->RTag == Link)
			p = p->rchild;
	}
	return OK;
}


【總的後序遍歷線索二叉樹程式碼】

#include <iostream>
#include <string.h>
#include <cstdio>
#include <stdlib.h>
using namespace std;
#define Status int 
#define OK 1
#define ERROR 0
#define TElemType char
typedef enum{
	Link,Thread
}PointerTag;//Link == 0 :指標 ,Thread == 1: 線索 
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode *lchild, *rchild; //左右孩子指標
	struct BiThrNode *parent;
	PointerTag LTag , RTag;            //左右標誌 
}BiThrNode, *BiThrTree;
BiThrTree pre;  //全域性變數，始終指向剛剛訪問過的結點。

Status visit(TElemType e){
	printf("%5c",e);
	return OK;
}
//char Vexch[20]={'H','D','A','$','$','C','$','B','$','$','G','F','$','E','$','$','$'};  
char Vexch[26]={'A','B','D','H','$','$','I','$','$','E','J','$','$','$','C','F','$','$','G','$','$'};  
int i=0;  
//二叉樹的建立  
Status CreatBiThrTree(BiThrTree &T,BiThrTree &p)  
{  
    if(Vexch[i++]=='$') T=NULL;  
    else  
    {  
        T= (BiThrTree)malloc(sizeof(BiThrNode)); 
        if(!T)  return 0;  
        T->data=Vexch[i-1];//生成根節點  
		T->parent = p;
        visit(T->data);
		T->LTag=Link; 
        CreatBiThrTree(T->lchild,T);//建立左子樹 
		T->RTag=Link; 
        CreatBiThrTree(T->rchild,T);//建立右子樹  
    }  
    return 1;  
}  

void PostThreading(BiThrTree p){
	if(p){
		PostThreading(p->lchild);     //左子樹線索化
		PostThreading(p->rchild);     //右子樹線索化 
		if(!p->lchild){               //沒有左孩子 
			p->LTag = Thread;         //前驅線索 
			p->lchild = pre;          //左孩子指標指向前驅 
		}
		if(pre && !pre->rchild){
			pre->RTag = Thread;       //後繼線索
			pre->rchild = p ;         //前驅右孩子指標指向後繼 
		}
		pre = p;
	}
}
//後序 遍歷線索二叉樹 
Status PostOrderTraverse_Thr(BiThrTree T ,Status(* visit)(TElemType e) ){
	BiThrTree p ;
	p = T;            // p指向根節點 
	pre=NULL;
	while(p != NULL){            //空樹 或者遍歷結束時 p == T
		while(p->LTag == Link )         // 走到最左結點  ||左結點
			p = p->lchild;
		 
		while(p->RTag == Thread ){      //訪問後繼       ||右結點
			visit(p->data);
			pre = p;
			p = p->rchild ;            
		}
		if(p == T){                     //是否是最後根節點
			visit(p->data); 
			break;
		}
		while(p && p->rchild == pre  ){ //訪問根         ||根節點
			visit(p->data);
			pre = p;
			p = p->parent;
		}
		if(p && p->RTag == Link)
			p = p->rchild;
	}
	return OK;
}
int main()
{
	BiThrTree PostT;
	printf("建立樹\n");
	pre = NULL;
	CreatBiThrTree(PostT,pre);
	printf("\n後序遍歷線索二叉樹\n");
	PostThreading(PostT);
	PostOrderTraverse_Thr(PostT , visit);
	printf("\n");
	return 0;
}

總結：
【問】為什麼用先序遍歷建樹後，可以用來中序遍歷線索化？
【答】先序遍歷建樹，只是一種建樹方式（當然可以用別的方法來建樹，但是數組裡的順序可能就要變化了），建完樹後，跟後面線索化無關。


【問】為什麼中序遍歷，先序遍歷，後序遍歷線上索化的時候，要用不同的線索化？
【答】因為中序，先序，後序，他們的前驅和後繼是不一樣的，根據程式碼也知道是不一樣。


【問】對於做題，畫已知二叉樹的前序、中序、後序線索二叉樹有什麼技巧嗎？

【答】可以先將 二叉樹前序、中序、後序遍歷 順序寫出來。再根據寫出來的順序對二叉樹進行線索化。

【問】接上，線索化的時候這麼亂，不知道線索改連到哪裡？

【答】每個結點左右各有一個指標，除了用於建樹的“藍色”線之外，我們只看紅色的線索這條線。每個結點只要是線索的部分，左邊就是指向排在該結點之前的那個結點，右邊就是指排在該節點之後的那個結點，這也就是為什麼要先把遍歷的順序提前寫好的原因。


相關推薦

資料結構之線索二叉樹的簡單實現

二叉樹的鏈式儲存時會有較多空間的浪費，當一顆有 n 個節點的二叉樹儲存共有2n個指標域，但是隻有n-1個被用到，所以剩下的n+1個都會被浪費掉，因此可以想一種辦法把剩餘的空間利用起來，線索二叉樹應運而生。 將二叉樹重新定義如下每個節點為下列形式 lchild l

Java版資料結構之線索二叉樹

簡介 中序線索化二叉樹 中序線索化遍歷 程式碼實現 public class MyThreadTree { int data;//結點權值 MyThreadTree leftTree;//左子樹 MyThread

【資料結構】線索二叉樹

【背景】 在具有n個結點二叉樹中，共有n+1個指標域空置不用。為此，A. j. Parlis 和C. Thornton 提出利用二叉數中這些空的鏈域來儲存結點前驅或後繼的地址資訊。即：若某個結點的left指標為空，則使該left指標指向該結點的前驅結點；若某個結點的right指標為空，則

資料結構之線索二叉樹的前序,中序和後序遍歷

BinaryTree線索化二叉樹>      二叉樹是一種非線性結構，在之前實現的二叉樹遍歷中不管是遞迴還是非遞迴用二叉樹作為儲存結構時只能取到該結點的左孩子和右孩子，不能得到該結點的前驅和後繼。為了儲存這種在遍歷中需要的資訊，同時也為了充分利用結點中的空指標域，我們

【資料結構】線索二叉樹的基本操作 構造 找前驅 找後繼

                     上圖所示的二叉連結串列，存在多個空指標域。假設一個二叉連結串列的結點數為n，則共有2n個指標域。而n個結點的二叉樹共有n-1條分支。所以空指標域的個數為：2n - (n-1) = n+1。可以在這n+1個空指標域中儲存結點的（以先序、

資料結構入門--線索二叉樹

當我們遍歷一棵二叉樹時，我們會得到整棵樹資料的一個序列（前or中or後），可以知道一個數據結點的前驅或者後繼是哪個結點。但是，對於每個結點的結構，我們只能從中得知某結點的左右孩子的資訊，要得到前驅/後繼結點的資訊就要遍歷一遍二叉樹，這樣豈不是很麻煩？我們能不能有

資料結構--樹--線索二叉樹（中序，前序，後序）

線索二叉樹 在遍歷二叉樹的時候，會有許多空指標域，這些空間不儲存任何事物，白白浪費了記憶體的資源。 那麼在做遍歷的時候，提前記錄下每個結點的前驅和後繼，這樣就更加節約了時間。                  [ lchild ] [ LTag ] [ data ] [ R

資料結構與演算法 -- 二叉樹鏈式詳解（（非）/遞迴遍歷，葉子個數，深度計算）

前言 PS：樹型結構是一種重要的非線性資料結構，教科書上一般都是樹與二叉樹，由此可見，樹和二叉樹是有區別和聯絡的，網上有人說二叉樹是樹的一種特殊形式，但經過查資料，樹和二叉樹沒有一個肯定的說法，但唯一可以肯定都是樹型結構。但是按照定義來看二叉樹並不是樹的一種特殊形式（下面解釋）。樹型資料結構的作

資料結構實驗之二叉樹六：哈夫曼編碼（SDUT 3345）

題解：離散中的“最小生成樹（最優樹）”。 #include <bits/stdc++.h> using namespace std; void qusort(int l, int r, int a[]) { int x = a[l]; int i = l, j =

資料結構實驗之二叉樹一：樹的同構 （SDUT 3340）

題解：把原本結構體的左右子樹的型別定義成 int 型，用來存放這個結點的左右子樹的編號，分別建造兩棵二叉樹，按個比較，如果在第二棵樹中沒有找到，那麼就不用在判斷了。 #include <bits/stdc++.h> using namespace std; struct node

資料結構實驗之二叉樹八：（中序後序）求二叉樹的深度（SDUT 2804）

#include <stdio.h> #include <stdlib.h> #include <string.h> struct node { char data ; struct node *l,*r; }; struct node *cr

資料結構實驗之二叉樹七：葉子問題（SDUT 3346）

#include <bits/stdc++.h> using namespace std; struct node { char data; struct node *lc, *rc; }; char a[100]; int num = 0; struct node

資料結構實驗之二叉樹四：（先序中序）還原二叉樹 （SDUT 3343）

#include <bits/stdc++.h> using namespace std; struct node { char data; struct node *lc, *rc; }; char a[100],b[100]; int n; struct node

資料結構實驗之二叉樹五：層序遍歷 （SDUT 3344）

#include <bits/stdc++.h> using namespace std; struct node { char data; struct node *lc, *rc; }; char s[505]; int num; struct node *cre

資料結構實驗之二叉樹三：統計葉子數（有返回值版）

Problem Description 已知二叉樹的一個按先序遍歷輸入的字元序列，如abc,de,g,f, (其中,表示空結點)。請建立二叉樹並求二叉樹的葉子結點個數。 Input 連續輸入多組資料，每組資料輸入一個長度小於50個字元的字串。 Output 輸出

資料結構實驗之二叉樹四：（先序中序）還原二叉樹

Problem Description 給定一棵二叉樹的先序遍歷序列和中序遍歷序列，要求計算該二叉樹的高度。 Input 輸入資料有多組，每組資料第一行輸入1個正整數N(1 <= N <=

資料結構實驗之二叉樹八：（中序後序）求二叉樹的深度

Problem Description 已知一顆二叉樹的中序遍歷序列和後序遍歷序列，求二叉樹的深度。 Input 輸入資料有多組，輸入T，代表有T組資料。每組資料包括兩個長度小於50的字串，第一個字串表示二叉樹的中序遍歷，第二個表示二叉樹的後序遍歷。 Output

資料結構作業11—二叉樹（函式題）

6-2 二叉樹求結點數 （15 分） 編寫函式計算二叉樹中的節點個數。二叉樹採用二叉連結串列儲存結構。 函式介面定義： int NodeCountOfBiTree ( BiTree T); 其中 T是二叉樹根節點的地址。 裁判測試程式樣例： //標頭檔案

資料結構作業11—二叉樹（選擇題）

2-1要使一棵非空二叉樹的先序序列與中序序列相同，其所有非葉結點須滿足的條件是：(2分) A.結點的度均為2 B.只有右子樹 C.結點的度均為1 D.只有左子樹 作者: 考研試卷 單位: 浙江大學 2-2若一棵二叉樹的後序遍歷

資料結構作業11—二叉樹（判斷題）

1-1若一個結點是某二叉樹的中序遍歷序列的最後一個結點，則它必是該樹的前序遍歷序列中的最後一個結點。 (2分) T F 作者: DS課程組 單位: 浙江大學 1-2若A和B都是一棵二叉樹的葉子結點，則存在這樣的二叉樹，其前序遍歷序列為…A…B