2. 程式人生 > >從頭到尾徹底理解KMP（2014年7月版）

從頭到尾徹底理解KMP（2014年7月版）

阿新 • • 發佈：2018-12-25

從頭到尾徹底理解KMP

作者：July
時間：最初寫於2011年12月，2014年7月21日晚10點 全部刪除重寫成此文。

1. 引言

    本KMP原文最初寫於2年多前的2011年12月，因當時初次接觸KMP，思路混亂導致寫也寫得非常混亂，如此，留言也是“罵聲”一片。所以一直想找機會重新寫下KMP，但苦於一直以來對KMP的理解始終不夠，故才遲遲沒有修改本文。

    然近期因在北京開了個演算法班，專門講解資料結構、面試、演算法，才再次仔細回顧了這個KMP，在綜合了一些網友的理解、以及跟我一起講演算法的兩位講師朋友曹博、鄒博的理解之後，寫了9張PPT，發在微博上。隨後，一不做二不休，索性將PPT上的內容整理到了本文之中。

    KMP本身不復雜，但網上大部分的文章（包括本文的2011年版本）把它講混亂了。下面，咱們從暴力匹配演算法講起，一步步從字串的字首字尾引入next陣列，接著利用next 陣列進行匹配，最後介紹KMP的一種擴充套件演算法，希望讓大家對KMP有一個清晰的瞭解。

2. 暴力匹配演算法

    咱們先來看暴力匹配演算法。假設現在文字串S匹配到 i 位置，模式串P匹配到 j 位置

  • 如果當前字元匹配成功（即S[i] == P[j]），則i++，j++，繼續匹配下一個字元；
  • 如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0，因為每次匹配失敗時，j 都被置為0，所以i = i+1，相當於失配時模式串P相對於文字串S向右移動一位。
    理清楚了暴力匹配演算法的流程及內在的邏輯，咱們可以寫出暴力匹配的程式碼，如下：
  1. int Violentmatch(char* s, char* p)  
  2. {  
  3.     int sLen = strlen(s);  
  4.     int pLen = strlen(p);  
  5.     int ans = -1;  
  6.     int i = 0;  
  7.     int j = 0;  
  8.     while (i < sLen && j < pLen)  
  9.     {  
  10.         if (s[i] == p[j])  
  11.         {  
  12.             //①如果當前字元匹配成功（即S[i] == P[j]），則i++，j++  
  13.             i++;  
  14.             j++;  
  15.         }  
  16.         else
  17.         {  
  18.             //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0  
  19.             i = i - j + 1;  
  20.             j = 0;  
  21.         }  
  22.     }  
  23.     if (j == pLen)  
  24.     {  
  25.         //匹配成功，返回模式串p在文字串s中的位置  
  26.         ans =  i - j;  
  27.     }  
  28.     return ans;  
  29. }  

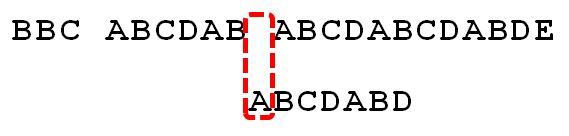
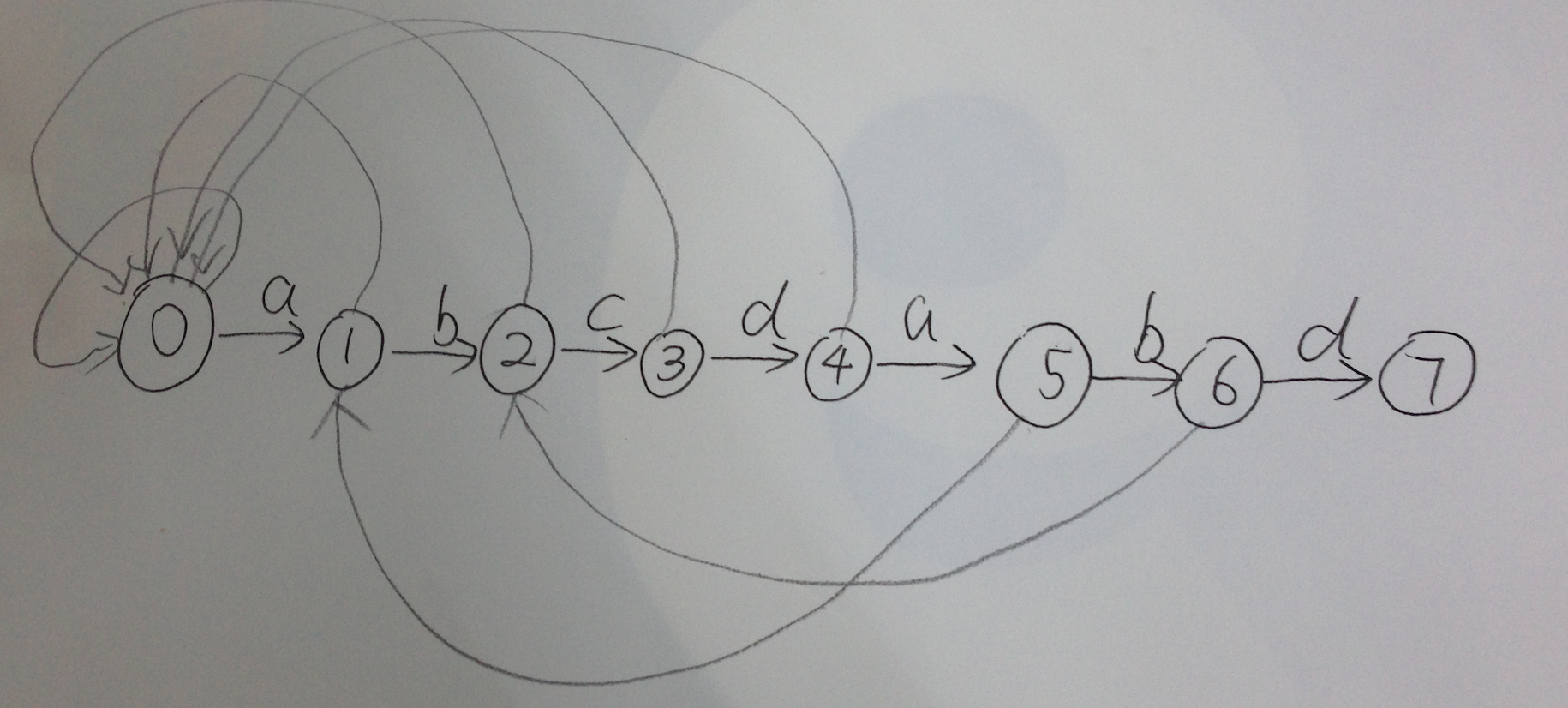
    舉個例子，如果給定文字串S“BBC ABCDAB ABCDABCDABDE”，和模式串T“ABCDABD”，現在要拿模式串P去跟文字串S匹配，整個過程如下所示：

    1. S[0]為B，P[0]為A，不匹配，執行第②條指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相當於模式串要往右移動一位（i=1，j=0）

    2. S[1]跟P[0]還是不匹配，繼續執行第②條指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），從而模式串不斷的向右移動一位（不斷的執行“令i = i - (j - 1)，j = 0”，i從2變到4，j一直為0）

3. 直到S[4]跟P[0]匹配成功（i=4，j=0），此時按照上面的暴力匹配演算法的思路，轉而執行第①條指令：“如果當前字元匹配成功（即S[i] == P[j]），則i++，j++”，可得S[i]為S[5]，P[j]為P[1]，即接下來S[5]跟P[1]匹配（i=5，j=1）

     

4. S[5]跟P[1]匹配成功，繼續執行第①條指令：“如果當前字元匹配成功（即S[i] == P[j]），則i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此進行下去

    

    5. 直到S[10]為空格字元，P[6]為字元D（i=10，j=6），因為不匹配，重新執行第②條指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相當於S[5]跟P[0]匹配（i=5，j=0）

     

6. 至此，我們可以看到，如果按照暴力匹配演算法的思路，儘管之前文字串和模式串已經分別匹配到了S[9]、P[5]，但因為S[10]跟P[6]不匹配，所以文字串回溯到S[5]，模式串回溯到P[0]，從而讓S[5]跟P[0]匹配。

    而S[5]肯定跟P[0]失配。為什麼呢？因為在之前第4步匹配中，我們已經得知S[5] = P[1] = B，而P[0] = A，即P[0] != P[1]，所以S[5]必定不等於P[0]，所以回溯過去必然會導致失配。那有沒有一種演算法，讓i 不往回退，只需要移動j 即可呢？

    答案是肯定的。這種演算法就是本文的主旨KMP演算法，它利用之前已經部分匹配這個有效資訊，保持i 不回溯，通過修改j 的位置，讓模式串儘量地移動到有效的位置。

3. KMP演算法

3.1 流程

    咱們首先給出KMP演算法的流程：
  • 假設現在文字串S匹配到 i 位置，模式串P匹配到 j 位置
    • 如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++，繼續匹配下一個字元；
    • 如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]，模式串P相對於文字串S向右移動了至少1位（換言之，當匹配失敗時，模式串向右移動的位數為：失配字元所在位置 - 失配字元對應的next 值，即移動的實際位數為：j - next[j]，且此值大於等於1）。
    轉換成程式碼表示，則是：
  1. int kmpSearch(char* s, char* p, int n)  
  2. {  
  3.     int i = 0;  
  4.     int j = 0;  
  5.     int pLen = strlen(p);  
  6.     while (i < n)  
  7.     {  
  8.         //①如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++  
  9.         if (j == -1 || s[i] == p[j])  
  10.         {  
  11.             i++;  
  12.             j++;  
  13.         }  
  14.         else
  15.         {  
  16.             //②如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]  
  17.             //next[j]即為j所對應的next值    
  18.             j = next[j];  
  19.         }  
  20.     }  
  21.     if (j == pLen)  
  22.         return i - j;  
  23.     else
  24.         return -1;  
  25. }  
    繼續拿之前的例子來說，當S[10]跟P[6]匹配失敗時，KMP不是簡單的如樸素匹配那樣把模式串右移一位，而是執行第②條指令：“如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]”，即j 從6變到2（後面我們將求得P[6]，即字元D對應的next 值為2），所以相當於向右移動的位數為j - next[j]位（j - next[j] = 6-2 = 4位）。
    向右移動4位後，S[10]跟P[2]繼續匹配。為什麼要向右移動4位呢，因為移動4位後，模式串中又有個“AB”可以繼續跟S[8]S[9]匹配，相當於在模式串中找相同的字首和字尾，然後根據字首字尾求出next 陣列，最後基於next 陣列進行匹配（不關心next 陣列怎麼求來的，只想看匹配過程是咋樣的，可直接跳到下文3.2.4節）。

3.2 步驟

  • ①尋找最長字首、字尾
    • 對於Pj = p0 p1 ...pj-1，尋找模式串Pj中長度最大且相等的字首和字尾
      • 即尋找滿足條件的最大的k，使得p0 p1 ...pk-1 = pj-k pj-k+1...pj-1。也就是說，k是模式串中各個子串的字首字尾的公共元素的長度，所以求最大的k，就是看某個子串的哪個字首字尾的公共元素最多。
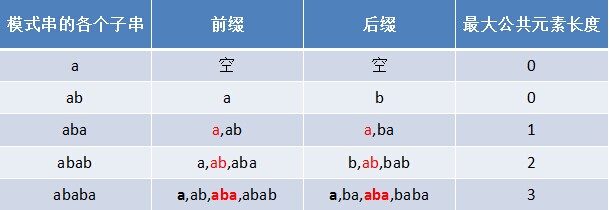
      • 舉個例子，如果給定的模式串為“abaabcaba”，那麼它的各個子串的字首字尾的公共元素的最大長度值如下表格所示：
  • ②求next陣列
    • 根據第①步驟中求得的各個字首字尾的公共元素的最大長度求得next 陣列，相當於前者右移一位且初值賦為-1，如下表格所示：
  • ③匹配失配，模式串向右移動的位數為：j - next[j]           
    • 注：j 是模式串中失配字元的位置，且 j 從0開始計數。
    KMP的next 陣列相當於告訴我們，模式串中的任意一個字元跟文字串中的某個字元匹配失配時，模式串下一步應該跳到哪個位置。如模式串中在j 處的字元跟文字串在i 處的字元匹配失配時，下一步用next [j] 處的字元繼續跟文字串匹配。     接下來，分別具體闡述上述3個步驟。

3.2.1 尋找最長字首字尾

    如果給定的模式串是：“ABCDABD”，從左至右遍歷整個模式串，其各個子串的字首字尾分別如下表格所示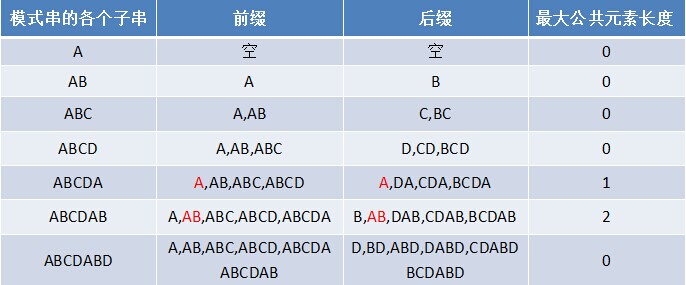：     也就是說，原字串對應的各個字首字尾的公共元素的最大長度表為（下簡稱《最大長度表》）：

3.2.2 基於《最大長度表》匹配

 因為模式串中首尾可能會有重複的字元，故可得出下述結論：
失配時，模式串向右移動的位數為：已匹配字元數 - 失配字元的上一位字元所對應的最大長度值

    下面，咱們就結合之前的《最大長度表》和上述結論，進行字串的匹配。如果給定文字串“BBC ABCDAB ABCDABCDABDE”，和模式串“ABCDABD”，現在要拿模式串去跟文字串匹配，如下圖所示：

        

  • 1. 因為模式串中的字元A跟文字串中的字元B、B、C、空格接連不匹配，所以模式串不斷的右移，直到模式串中的字元A跟文字串的第5個字元A匹配成功：

  • 2. 繼續往後匹配，當模式串最後一個字元D跟文字串匹配時失配，顯而易見，模式串需要向右移動。但向右移動多少位呢？因為此時已經匹配的字元數為6個（ABCDAB），然後根據《最大長度表》可得字元B對應的長度值為2，所以根據之前的結論，可知需要向右移動6 - 2 = 4 位。
  • 3. 模式串向右移動4位後，發現C處再度失配，因為此時已經匹配了2個字元（AB），且上一個字元B對應的最大長度值為0，所以向右移動：2 - 0 =2 位。
           
  • 4. A與空格失配，向右移動1 位。
  • 5. 繼續比較，發現D與C 失配，故向右移動的位數為：已匹配的字元數6減去上一位字元B對應的最大長度2，即向右移動6 - 2 = 4 位。
           
  • 6. 經歷第4步後，發現匹配成功，過程結束。

          

3.2.3 根據《最大長度表》求出next 陣列

    由上文，我們已經知道，字串“ABCDABD”各個字首字尾的最大公共元素長度分別為：

    而且，根據這個表可以得出下述結論

  • 失配時，模式串向右移動的位數為：已匹配字元數 - 失配字元的上一位字元所對應的最大長度值
    上文利用這個表和結論進行匹配時，我們發現，當匹配到一個字元失配時，其實沒必要考慮當前失配的字元，更何況我們每次失配時，都是看的失配字元的上一位字元對應的最大長度值。如此，便引出了next 陣列。     給定字串“ABCDABD”，可求得它的next 陣列如下：

    把next 陣列跟之前求得的最大長度表對比後，不難發現，next 陣列相當於“最大長度值” 整體向右移動一位，然後初始值賦為-1。意識到了這一點，你會驚呼原來next 陣列的求解竟然如此簡單！

    換言之，對於給定的模式串：ABCDABD，它的最大長度表及next 陣列分別如下：


    根據最大長度表求出了next 陣列後，從而有

失配時，模式串向右移動的位數為：失配字元所在位置 - 失配字元對應的next 值

    而後，你會發現，無論是基於《最大長度表》的匹配，還是基於next 陣列的匹配，兩者得出來的向右移動的位數是一樣的。

    接下來，咱們來寫程式碼求下next 陣列。

    基於之前的理解，可知計算next 陣列的方法可以採用遞推：

  • 如果對於值k，已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1，相當於next[j] = k。
    • 此意味著什麼呢？究其本質，next[j] = k 代表 j 之前的模式串中，有長度為k 的相同字首和字尾。有了這個next 陣列，在KMP匹配中，當模式串字尾中j 處的字元失配時，模式串向右移動j - next[j] 位。

舉個例子，如下圖，根據模式串“ABCDABD”的next 陣列可知失配位置的字元D對應的next 值為2，代表字元D前有長度為2的相同字首和字尾（這個相同的字首字尾即為“AB”），失配後，模式串需要向右移動j - next [j] = 6 - 2 =4位。

向右移動4位後，模式串中的字元C繼續跟文字串匹配。

  • 下面的問題是：已知next [j]，如何求出next [j + 1]呢？

    對於pattern的前j 個序列字元：

  • 若pattern[k] == pattern[j]，則next[j + 1 ] = next [j] + 1 = k + 1；
  • 若pattern[k ] ≠ pattern[j]，如果此時pattern[ next[k] ] == pattern[j ]，則next[ j ] =  next[k] + 1，否則重複此過程。 相當於在字元p[k+1]之前不存在字首"p0 p1, …, pk-1 pk"跟字尾“pj-k pj-k+1, …, pj-1 pj"相等，那麼是否可能存在另一個值t < k + 1，使得長度更小的字首 “p0 p1, …, pt-1” 等於長度更小的字尾 “pj-t pj-t+1…pj-1” 呢？這個t 便是next[k]，此相當於利用next 函式值進行P串字尾跟P串字首的匹配。
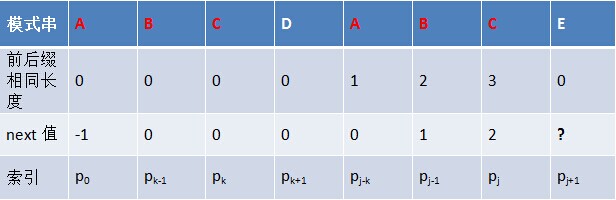
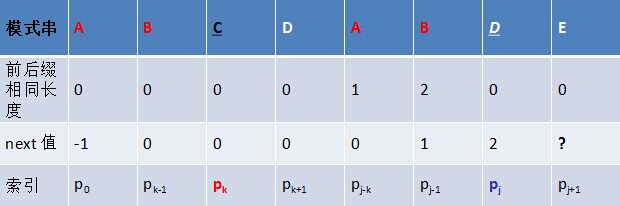
   一般的文章或教材可能就此一筆帶過，但大部分的初學者可能還是不能很好的理解上述求解next 陣列的原理，故接下來，我再舉個例子說明下。     如下圖所示，假定給定模式串ABCDABCE，且已知next [j] = k（相當於“p0 pk-1” = “pj-k pj-1” = AB，可以看出k為2），現要求next [j + 1]等於多少？因為pk = pj = C，所以next[j + 1] = next[j] + 1 = k + 1（可以看出next[j + 1] = 3）。代表字元E前的模式串中，有長度k+1 的相同字首字尾。

    但如果pk != pj 呢？說明“p0 pk-1 pk”  ≠ “pj-k pj-1 pj”。換言之，當pk != pj後，字元E前有多大長度的相同字首字尾呢？很明顯，因為C不同於D，所以ABC 跟 ABD不相同，即字元E前的模式串沒有長度為k+1的相同字首字尾，也就不能再簡單的令：next[j + 1] = next[j] + 1 。所以，咱們只能去尋找長度更短一點的相同字首字尾。

    咱們換個角度思考這個問題，類似KMP的匹配思路，當p0 p1, ..., pj 跟主串s0 s1, ..., si匹配時，如果模式串在j處失配，則模式串需要向右移動j - next[j]位，相當於j = next [j]。     現在字首“p0 pk-1 pk”  去跟字尾 “pj-k pj-1 pj”匹配，發現在pk處匹配失敗，那麼字首需要向右移動多少位呢？根據已經求得的字首各個字元的next 值，可得字首應該向右移動k - next[k]位，相當於k = next[k]。若移動之後，pk‘ = pj，則代表字元E前存在長度為next[k] + 1的相同字首字尾，否則繼續遞迴k‘ = next [k‘]，直到next [k’] = 0。     舉個例子如下：
模式串的字尾：ABD
模式串的字首：ABC
字首右移兩位：     ABC
    求next 陣列的程式碼如下所示：
  1. void getNext(char* p,int next[])  
  2. {  
  3.     int pLen = strlen(p);  
  4.     next[0] = -1;  
  5.     int k = -1;  
  6.     int j = 0;  
  7.     while (j < pLen - 1)  
  8.     {  
  9.         //p[k]表示字首，p[j]表示字尾
  10.         if (k == -1 || p[j] == p[k])   
  11.         {  
  12.             ++j;  
  13.             ++k;  
  14.             next[j] = k;  
  15.         }  
  16.         else
  17.         {  
  18.             k = next[k];  
  19.         }  
  20.     }  
  21. }  

3.2.4 基於《next 陣列》匹配

    下面，我們來基於next 陣列進行匹配。

    還是給定文字串“BBC ABCDAB ABCDABCDABDE”，和模式串“ABCDABD”，現在要拿模式串去跟文字串匹配，如下圖所示：

    在正式匹配之前，讓我們來再次回顧下上文2.1節所述的KMP演算法的匹配流程：

  • “假設現在文字串S匹配到 i 位置，模式串P匹配到 j 位置
    • 如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++，繼續匹配下一個字元；
    • 如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]，模式串P相對於文字串S向右移動了至少1位（換言之，當匹配失敗時，模式串向右移動的位數為：失配字元所在位置 - 失配字元對應的next 值，即移動的實際位數為：j - next[j]，且此值大於等於1）。”
  • 1. 最開始匹配時
    • P[0]跟S[0]匹配失敗
      • 所以執行“如果j != -1，且當前字元匹配失敗（即S[i] != P[j]），則令 i 不變，j = next[j]”，所以j = -1，故轉而執行“如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++”，得到i = 1，j = 0，即P[0]繼續跟S[1]匹配。
    • P[0]跟S[1]又失配，j再次等於-1，i、j繼續自增，從而P[0]跟S[2]匹配。
    • P[0]跟S[2]失配後，P[0]又跟S[3]匹配。
    • P[0]跟S[3]再失配，直到P[0]跟S[4]匹配成功，開始執行此條指令的後半段：“如果j = -1，或者當前字元匹配成功（即S[i] == P[j]），都令i++，j++”。
  • 2. P[1]跟S[5]匹配成功，P[2]跟S[6]也匹配成功, ...，直到當匹配到字元D時失配（即S[10] != P[6]），由於 j 從0開始計數，故數到失配的字元D時 j 為6，且字元D對應的next 值為2，所以向右移動的位數為：j - next[j] = 6 - 2 =4 位

  • 3. 向右移動4位後，C再次失配，向右移動：j - next[j] = 2 - 0 = 2 位

  • 4. 移動兩位之後，A 跟空格不匹配，再次後移1 位

  • 5. D處失配，向右移動 j - next[j] = 6 - 2 = 4 位
  • 6. 匹配成功，過程結束。

    匹配過程一模一樣。也從側面佐證了，next 陣列確實是只要將各個最大字首字尾的公共元素的長度值右移一位，且把初值賦為-1 即可。

3.2.5 基於《最大長度表》與基於《next 陣列》等價

    其實，利用next 陣列進行匹配失配時，模式串向右移動 j - next [ j ] 位，等價於已匹配字元數 - 失配字元的上一位字元所對應的最大長度值。為什麼呢？

  1. j 從0開始計數，那麼當數到失配字元時，j 的數值就是已匹配的字元數；
  2. 由於next 陣列是由最大長度值表整體向右移動一位（且初值賦為-1）得到的，那麼失配字元的上一位字元所對應的最大長度值，即為當前失配字元的next 值。

    那為何本文不直接利用next 陣列進行匹配呢？因為next 陣列不好求，而一個字串的字首字尾的公共元素的最大長度值很容易求，例如若給定模式串“ababa”，要你求其next 陣列，則乍一看，無從求起。而如果你求其字首字尾公共元素的最大長度，則很容易得出是：0 0 1 2 3，如下表格所示：

    

    然後這5個數字 全部整體右移一位，且初值賦為-1，即得到其next 陣列：-1 0 0 1 2。

3.2.6 next 陣列與有限狀態自動機

    next 負責把模式串向前移動，且當第j位不匹配的時候，用第next[j]位和主串匹配，就像打了張“表”。此外，next 也可以看作有限狀態自動機的狀態，在已經讀了多少字元的情況下，失配後，前面讀的若干個字元是有用的。


3.2.7 next 陣列的優化

   行文至此，咱們全面瞭解了暴力匹配的思路、KMP演算法的原理、流程、流程之間的內在邏輯聯絡，以及next 陣列的簡單求解（《最大長度表》整體右移一位，然後初值賦為-1）和程式碼求解，最後基於《next 陣列》的匹配，看似洋洋灑灑，清晰透徹，但以上忽略了一個小問題。

    當同一個字元大量重複出現的時候，會發生什麼現象呢？例如，當模式串和文字串如下所示時：

  • 模式串：aaaaa
  • 文字串：aaaabaaaabaaaab

    KMP也將顯得有心無力，跟暴力匹配一樣了。

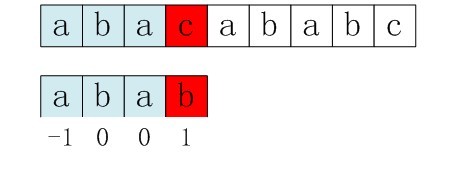
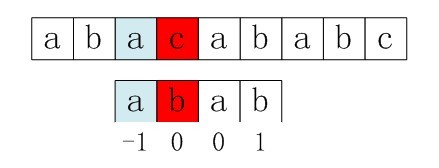
    再比如，如果用之前的next 陣列方法求模式串“abab”的next 陣列，可得其next 陣列為-1 0 0 1（0 0 1 2整體右移一位，初值賦為-1），當它跟下圖中的文字串去匹配的時候，發現b跟c失配，於是模式串右移j - next[j] = 3 - 1 =2位。

    右移2位後，b又跟c失配。事實上，因為在上一步的匹配中，已經得知p[3] = b，與s[3] = c失配，而右移兩位之後，讓p[ next[3] ] = p[1] = b 再跟s[3]匹配時，必然失配。問題出在哪呢？

    問題出在不該出現p[j] = p[ next[j] ]。為什麼呢？因為在p[j] != p[i] 的時候，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然導致後一步匹配失敗，所以不能允許p[j] = p[ next[j ]]。所以，咱們得修改下求next 陣列的程式碼。

  1. //優化過後的next 陣列求法
  2. void getNextval(char* p, int next[])  
  3. {  

  4. 相關推薦

    從頭到尾徹底理解KMP（2014年7月版）

    從頭到尾徹底理解KMP 作者：July時間：最初寫於2011年12月，2014年7月21日晚10點 全部刪除重寫成此文。 1. 引言     本KMP原文最初寫於2年多前的2011年12月，因當時初次接觸KMP，思路混亂導致寫也寫得非常混亂，

    從頭到尾徹底理解KMP（2014年8月22日版）

    從頭到尾徹底理解KMP 作者：July 時間：最初寫於2011年12月，2014年7月21日晚10點 全部刪除重寫成此文，隨後的半個多月不斷反覆改進。後收錄於新書《程式設計之法：面試和演算法心得》第4.4節中。 1. 引言     本KMP原

    從頭到尾徹底理解KMP（2014年8月22日版）(轉載)

    從頭到尾徹底理解KMP 作者：July 時間：最初寫於2011年12月，2014年7月21日晚10點 全部刪除重寫成此文，隨後的半個多月不斷反覆改進。後收錄於新書《程式設計之法：面試和演算法心得》第4.4節中。

    iteye新聞熱點月刊總第60期（2013年2月版）發布了

    mdi 發布 mtu odi odm mdk .com dex mtk 2014%E5%B9%B48%E5%A4%A7%E7%A7%91%E6%8A%80%E6%BD%AE%E6%B5%81 http://www.zcool.com.cn/collection/ZMTY5

    KMP之一：從頭到尾徹底理解KMP演算法（2014年8月1日版）

    作者：July 時間：最初寫於2011年12月，2014年7月21日晚10點 全部刪除重寫成此文。 1. 引言     本KMP原文最初寫於2年多前的2011年12月，因當時初次接觸KMP，思路混亂導致寫也寫得非常混亂，如此，留言也是“罵聲”一片。所以一直想找機會重新寫下KMP，但苦於一直以來對KMP的理

    從頭到尾徹底理解KMP（轉載自July）

    從頭到尾徹底理解KMP 作者：July 時間：最初寫於2011年12月，2014年7月21日晚10點 全部刪除重寫成此文，隨後的半個多月不斷反覆改進。 1. 引言     本KMP原文最初寫於2年多前的2011年12月，因當時初次接觸KMP，思路混亂導致寫也寫得混亂，如此，留言也

    北京亞控筆試題目（2014年10月9日）

    1 右值左值 C/C++語言中可以放在賦值符號左邊的變數，左值表示儲存在計算機記憶體的物件，左值相當於地址值。右值：當一個符號或者常量放在操作符右邊的時候，計算機就讀取他們的“右值”，也就是其代表的真實值，右值相當於資料值 左值和右值是相對於賦值表示式而言的。左值是能出現在

    python--for循環（2017年7月13日）

    運行 continue break 判斷語句 -- for循環 cnblogs 一次循環 bre on old boy 斷點 ---調試---可以查看程序運行的具體操作流程。 continue --跳出本次循環，繼續到下一次循環。 break -- 結束整個循環。 ----

    [2014年7月]程式語言排行榜(統計資料源於TIOBE)

    茶話匯已介紹過多期TIOBE釋出的程式語言排行榜，下面就來看看TIOBE於2014年7月份釋出的程式語言排行榜。 導讀（根據榜單識別出來的關鍵資訊）： – 排名前三的還是 C、Java、Objective-C； – 蘋果公司上個月剛推出的新程式語言 Swif，在本月就排在了第 16 位； – 現在

    學習記錄（2018年7月25日）

     1、編寫一個C函式,將句子中的單詞位置倒置,而不改變單詞內部結構. #include <stdio.h> #include <stdlib.h> #include <string.h> void str_rev(char *str,

    IDEA、PyCharm啟用碼（2019年5月到期）

    347DQLVO7L-eyJsaWNlbnNlSWQiOiIzNDdEUUxWTzdMIiwibGljZW5zZWVOYW1lIjoi5b285bK4IHNvZnR3YXJlMSIsImFzc2lnbmVlTmFtZSI6IiIsImFzc2lnbmVlRW1haWwiOiI

    windows下caffe介面的匯入（2018年7月）

    matlab中caffe的配置 第一步：將上一步生成的matcaffe加入matlab的路徑中，直接在setpath裡面設定 並將D:\caffe2\caffe-master\Build\x64\Release該路徑放到【系統變數】-【Path】中

    高薪誠聘熟悉ABP框架的.NET高階開發工程師（2016年7月28日重發）

    招聘單位是ABP架構設計交流群(134710707)群主陽銘所在的公司-上海運圖貿易有限公司 招聘崗位：.NET高階開發工程師工作地點：上海-普陀區 【公司情況】上海運圖貿易有限公司，是由易迅網的創始人卜廣齊投資2500萬美金成立的O2O汽車電商公司，由卜廣齊親自任CEO，是全國最大的自營新車電商，目前已

    學習ECMAScript（2017年7月27日）

    一元運算子 Delete delete 運算子刪除對開發者新增的屬性或方法的引用，不能刪除系統的屬性或方法引用。 Void void 運算子對任何值返回 undefined。該運算子通常用於避免輸出不應該輸出的值。 例如，從 HTML 的 <a> 元素呼叫 Ja

    我的閱讀清單（2018年3月開始）

    主要是為了督促自己，記錄自己的閱讀記錄，更好的堅持。 1、《意志力是訓練出來的》 菲爾圖（2018年3月） 2、《Effective java》中文版 第2版 Joshua Bloch（2018年4月） 3、《深入分析Java Web技術內蒙》許令波著（2018.4.1

    輸入阿拉伯數字（整數），輸出相應的中文（美團網2014年9月16日筆試題目之中的一個）

    ++i 方式 data ++ name int end == pri 2014年9月16日，美團網南京筆試題之中的一個。原要求是輸入整數的位數最多為四位。這裏擴展為12為，即最高到千億級別。 思路及步驟： 1 判別輸入是否合法，並過濾字符串最前面的‘0’。 2 將字符串

    ZOJ 3810 A Volcanic Island （2014年牡丹江賽區網絡賽B題）

    amp fin function for sca mod zju dsm unsigned 1.題目描寫敘述：點擊打開鏈接 2.解題思路：本題是四色定理的模板題。只是有幾種情況要提前特判一下：n==1直接輸出，1<n<5時候無解，n==6時候套用模板會

    2014年8月25日，收藏家和殺手——面向對象的C++和C（一）

    creat os x tracking -m end gin 知識 數據 我們 近期事情特別多，睡眠也都非常晚，有點精神和身體混亂的感覺，所以想寫寫技術分析文章。讓兩者的我都調整一下。這篇技術分析文章是一直想寫的，當前僅僅是開篇，有感覺的時候就寫寫，屬於拼湊而成，興

    從flask視角理解angular（三）ORM VS Service

    不同 style 實現 component con 如何 怎麽辦 mode string 把獲取模型數據的任務重構為一個單獨的服務，它將提供英雄數據，並把服務在所有需要英雄數據的組件間共享。 @Injectable() export class HeroServic

    從flask視角理解angular（二）Blueprint VS Component

    location class 表示 one camel 區別 標準 wak void Component類似flask app下面的每個blueprint。 import ‘rxjs/add/operator/switchMap‘; import { Co