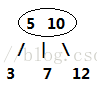前言

      紅黑樹，對不少人來說是個比較頭疼的名字，在網上搜資料也很少有講清楚其演變來源的，多數一上來就給你來五條定義，紅啊黑啊與根節點距離相等之類的，然後就開始進行旋轉、插入、刪除這些操作。一通操作下來，連紅色和黑色怎麼來的，是什麼含義，有什麼作用都雲裡霧裡的，能搞清楚就怪了。

      本文介紹紅黑樹，暫時不涉及任何程式碼，只是幫助你理解紅黑樹的演變來源，樹結構中紅黑色具體含義，保證你理解了過後，再去看什麼旋轉插入的東西，要清晰得多。換句話說，理解本文要描述的內容是從程式碼級理解紅黑樹的基礎。

      開始之前，我還是懇請你保持耐心，一步一步仔細看完，浮躁的話真的做不好任何事情。

正文

      紅黑樹的起源，自然是二叉查詢樹了，這種樹結構從根節點開始，左子節點小於它，右子節點大於它。每個節點都符合這個特性，所以易於查詢，是一種很好的資料結構。但是它有一個問題，就是容易偏向某一側，這樣就像一個連結串列結構了，失去了樹結構的優點，查詢時間會變壞。

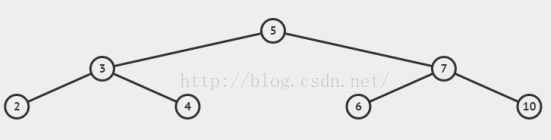
      所以我們都希望樹結構都是矮矮胖胖的，像這樣：

      而不是像這樣：

     在這種需求下，平衡樹的概念就應運而生了。

      紅黑樹就是一種平衡樹，它可以保證二叉樹基本符合矮矮胖胖的結構，但是理解紅黑樹之前，必須先了解另一種樹，叫2-3樹，紅黑樹背後的邏輯就是它。

    好吧來看2-3樹吧。

    2-3樹是二叉查詢樹的變種，樹中的2和3代表兩種節點，以下表示為2-節點和3-節點。

    2-節點即普通節點：包含一個元素，兩條子連結。

    3-節點則是擴充版，包含2個元素和三條連結：兩個元素A、B，左邊的連結指向小於A的節點，中間的連結指向介於A、B值之間的節點，右邊的連結指向大於B的節點。

2-節點：             3-節點： 

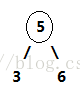
      在這兩種節點的配合下，2-3樹可以保證在插入值過程中，任意葉子節點到根節點的距離都是相同的。完全實現了矮胖矮胖的目標。怎麼配合的呢，下面來看2-3樹的構造過程。

      所謂構造，就是從零開始一個節點一個節點的插入。

      在二叉查詢樹中，插入過程從根節點開始比較，小於節點值往右繼續與左子節點比，大於則繼續與右子節點比，直到某節點左或右子節點為空，把值插入進去。這樣無法避免偏向問題。在2-3樹中，插入的過程是這樣的。

      如果將值插入一個2-節點，則將2-節點擴充為一個3-節點。

      如果將值插入一個3-節點，分為以下幾種情況。

      (1).3-節點沒有父節點，即整棵樹就只有它一個三節點。此時，將3-節點擴充為一個4-節點，即包含三個元素的節點，然後將其分解，變成一棵二叉樹。

      此時二叉樹依然保持平衡。

      (2).3-節點有一個2-節點的父節點，此時的操作是，3-節點擴充為4-節點，然後分解4-節點，然後將分解後的新樹的父節點融入到2-節點的父節點中去。

      (3).3-節點有一個3-節點的父節點，此時操作是：3-節點擴充為4-節點，然後分解4-節點，新樹父節點向上融合，上面的3-節點繼續擴充，融合，分解，新樹繼續向上融合，直到父節點為2-節點為止，如果向上到根節點都是3-節點，將根節點擴充為4-節點，然後分解為新樹，至此，整個樹增加一層，仍然保持平衡。

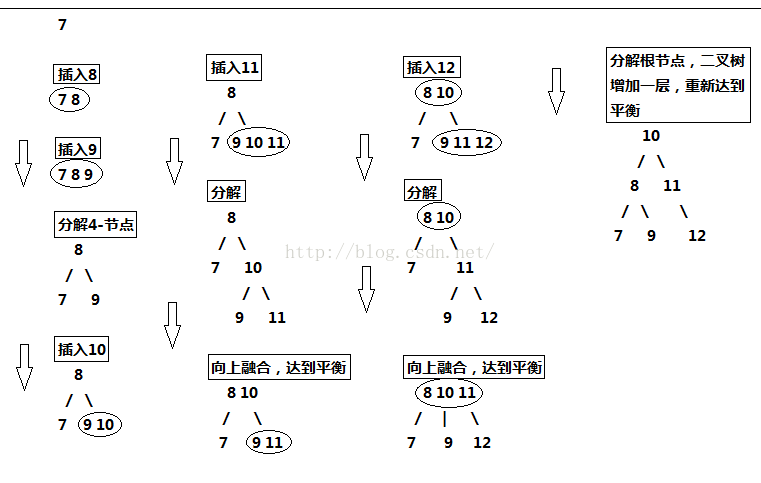
      第三種情況稍微複雜點，為了便於直觀理解，現在我們從零開始構建2-3樹，囊括上面所有的情況，看完所以步驟後，你也可以自己畫一畫。

      我們將{7,8,9,10,11,12}中的數值依次插入2-3樹，畫出它的過程：

      所以，2-3樹的設計完全可以保證二叉樹保持矮矮胖胖的狀態，保持其效能良好。但是，將這種直白的表述寫成程式碼實現起來並不方便，因為要處理的情況太多。這樣需要維護兩種不同型別的節點，將連結和其他資訊從一個節點複製到另一個節點，將節點從一種型別轉換為另一種型別等等。

      因此，紅黑樹出現了，紅黑樹的背後邏輯就是2-3樹的邏輯，但是由於用紅黑作為標記這個小技巧，最後實現的程式碼量並不大。(但是，要直接理解這些程式碼是如何工作的以及背後的道理，就比較困難了。所以你一定要理解它的演化過程，才能真正的理解紅黑樹)

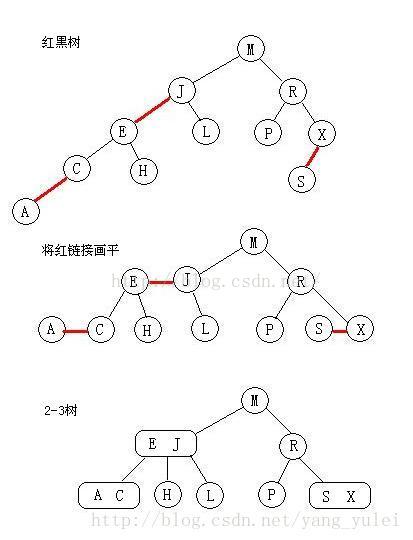
      我們來看看紅黑樹和2-3樹的關聯，首先，最檯面上的問題，紅和黑的含義。紅黑樹中，所有的節點都是標準的2-節點，為了體現出3-節點，這裡將3-節點的兩個元素用左斜紅色的連結連線起來，即連線了兩個2-節點來表示一個3-節點。這裡紅色節點標記就代表指向其的連結是紅連結，黑色標記的節點就是普通的節點。所以才會有那樣一條定義，叫“從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點”，因為紅色節點是可以與其父節點合併為一個3-節點的，紅黑樹實現的其實是一個完美的黑色平衡，如果你將紅黑樹中所有的紅色連結放平，那麼它所有的葉子節點到根節點的距離都是相同的。所以它並不是一個嚴格的平衡二叉樹，但是它的綜合性能已經很優秀了。

      借一張別人的圖來看：

紅連結放平：

      所以，紅黑樹的另一種定義是滿足下列條件的二叉查詢樹：
⑴紅連結均為左連結。
⑵沒有任何一個結點同時和兩條紅連結相連。(這樣會出現4-節點)
⑶該樹是完美黑色平衡的，即任意空連結到根結點的路徑上的黑連結數量相同。

      理解了這個過程以後，再去看紅黑樹的各種嚴格定義，以及其插入，刪除還有旋轉等操作，相信你腦子裡的思路會清晰得多的。