本部落格參考知乎王晉東不在家的知乎文章以及論文原文得來

論文地址:https://arxiv.org/abs/1705.10667

王晉東不在家知乎主頁：https://www.zhihu.com/people/jindongwang/activities

背景

對抗學習已經被嵌入到深度網路中通過學習到可遷移的特徵進行域適應，並取得了不錯的成果，作者指出當前的一些對抗域適應方法仍然存在問題：1.只是獨立的對齊特徵f而沒有對齊標籤，而這往往是不充分的 2.當資料分佈體現出複雜的多模態結構時，對抗性自適應方法可能無法捕獲這種多模態結構，換句話說即使網路訓練收斂，判別器完全被混淆，分辨不出樣本來自哪個域，也無法保證此時源域和目標域足夠相似（沒有捕獲到資料的多模態結構）。 3.條件域判別器中使用最大最小優化方法也許存在一定的問題，因為與判別器強制不同的樣本具有相同的重要性，然而那些不確定預測的難遷移樣本也許會對抗適應產生不良影響。 作者提出的條件對抗域適應網路（CDANs）在一定程度上解決了這三個問題，針對1，CDAN通過對齊特徵-類別的聯合分佈解決，針對2，CDAN使用了Multilinear Conditioning多線性調整的方法來解決，針對3，作者提出了在目標函式中新增Entropy Conditioning熵調整來解決。

CDAN結構

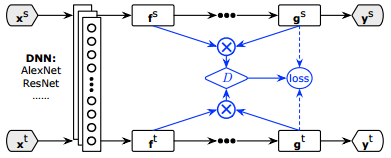
上圖框架很好理解，框架的前段通過深度神經網路，比如Alexnet/ResNet對源域和目標域提取特徵f，然後得出預測結果g，g得出預測標籤，CDAN的框架與之前一篇論文《Simultaneous Deep Transfer Across Domains and Tasks》相似，只是在CDAN中將預測結果g與特徵f的聯合起來輸入到判別器D中， $\bigotimes$

表示的是使用多線性對映對f和g進行聯結。

在最近的條件生成對抗網路Conditional Generative Adversarial Networks(CGAN)中揭示了不同的分佈可以在相關資訊上調整生成器和判別器匹配的更好，例如：將標籤和附屬狀態關聯。CGAN可以在具有高可變性和多模態的分佈資料集中生成全域性一致影象。受到CGAN的啟示，作者觀察到在對抗域適應中，分類器預測結果g中攜帶了潛在的揭露了多模態結果的判別資訊，這可以在對齊特徵f時用於調整，從而在網路訓練過程中捕獲多模態資訊。通過連線變數 $h$

= ( f , g ) h=(f,g) 在分類器預測結果g上調整域判別器D，這樣可以解決上面所說的前兩個問題，而最簡單的一種連線方式就是 $f\bigoplus g$，然後將 $f\bigoplus g$丟入到域判別器D中，這種連線策略被現有的CGANs方法中廣泛的採用，然而在這種連線策略中，f和g是相互獨立的，導致了不能很好的捕捉到特徵與分類器預測結果之間的相乘互動，而這對於域適應是至關重要的，作為結果，分類器預測中傳達的多模態資訊不能被充分利用來匹配複雜域的多峰分佈。

多線性調整

至於為什麼用多線性對映，而不是上面提到的 $f\bigoplus g$呢？假設線性對映 $\phi(x)=x$和具有C類別數的one-hot標籤變數y，均值對映 $E_{xy}[x\bigoplus y] = E_x[x]\bigoplus E_y[y]$分別獨立的計算了x和y的均值，相反，均值對映 $E_{xy}[x\bigotimes y] = E_x[x|y=1]\bigoplus .... \bigoplus E_x[x|y=C]$計算了每一個C類條件分佈 $P(x|y)$的均值。比 $f\bigoplus g$好的是，多線性對映模擬了不同變數之間的乘法相互作用，並且多線性對映相比於 $f\bigoplus g$最大的優勢就是多線性對映 $f\bigotimes g$能夠完全捕捉到複雜資料分佈後的多模態結構。而多線性對映的一個劣勢則是維度爆炸，假如 $d_f/d_g$表示向量f和g的維度，那麼線性對映 $f\bigotimes g$的維度則是 $d_f*d_g$，二者的維度通常較大，因此很容易發生維度爆炸。文章通過隨機方法來解決這個問題。即隨機抽取f和g上的某些維度做多線性對映： $T_{\bigodot}(f,g) = \frac{1}{\sqrt{d}} (R_f f) \bigodot (R_g g)$，其中 $\bigodot$表示逐元素運算， $R_f /R_g$分別表示隨機矩陣，其只被取樣一次並且在訓練過程中固定。d則是需要取樣的維度。經過作者論證，在 $T_{\bigodot}$上進行內積近似的等於 $T_{\bigotimes}$上進行內積，因此，可以直接採用 $T_{\bigodot}$用於計算以方便效率。在文中，作者採用了一下隨機取樣策略：

即當f和g的維度相乘大於4096時，採用隨機策略進行多線性對映，小於就使用正常的多線性對映。

熵調整

就像上面所說，條件域判別器中使用最大最小優化方法也許存在一定的問題，因為與判別器強制不同的樣本具有相同的重要性，然而那些不確定預測的難遷移樣本也許會對抗適應產生不良影響。為了減少這種影響，作者通過熵 $H(g) = - \sum_{c=1}^C g_c log(g_c)$來定量分類器預測結果的不確定性，而預測結果的確定性則可以被計算為 $e^{-H(g)}$。然後通過這種基於熵的確定性策略調整域判別器，然後最終的CDAN使用minimax的目標函式則為：

其實就是正常的minimax在其中加入了熵作為權重係數進行調整。

參考

Long M, Cao Z, Wang J, et al. Conditional Adversarial Domain Adaptation. NIPS 2018.

Hoffman J, Tzeng E, Darrell T, et al. Simultaneous Deep Transfer Across Domains and Tasks[J]. 2015, 30(31):4068-4076.