基於基本蟻群演算法解決連續優化問題

相關連結

TSP_旅行商問題-基本蟻群演算法

基本蟻群演算法解決連續優化問題基本流程

用一個螞蟻代表一個可行解，一個螞蟻含有的資訊包括各變數值；
1、確定迭代週期；
2、確定螞蟻數；
$\quad$2.a、隨機初始化蟻群，記錄蟻群中的最優解；
$\quad$2.b、進入迴圈，將已初始化的螞蟻分為兩種；
$$

$\quad$$\quad$2.b.a、一種是上一次蟻群中的最優解，搜尋在最優解附近搜尋；
可行解格式{$自變數_1$、$自變數_2$、$\cdots$、$自變數_n$}
X={$x_1$、$x_2$、$\cdots$、$x_n$}

$$x_i=x_i+\omega*L$$ 或
$$x_i=x_i-\omega*L$$ 擇優錄取吧，每次迴圈後， $\omega$要變小；
$\quad$ $\quad$2.b.b、另一種是非最優解，有一定概率向最優解進化；
$$P=\frac{e^{mess_{best}-mess_i}}{e^{mess_{best}}}$$
$mess_{best}$最優解螞蟻的資訊素濃度；
$mess_i$當前螞蟻的資訊素濃度；
$\quad$ $\quad$ $\quad$2.b.b.a、向最優解移動：
$$x_i=x_i+u*(x_{best}-x_{i})$$
$\quad$ $\quad$ $\quad$2.b.b.b、自己搜尋移動：
$$x_i=x_i+dx*rand(-1,1)$$
$\quad$2.c、更新資訊素
$$mess_i=(1-p)*mess_i+k*a^{-f(X)}$$

引數設定

最大迭代週期 T = 200;
螞蟻數量 ant_size = 25;
資訊素衰退因子 p = 0.9;
步長係數 $\omega$ = 1，隨著迭代的進行變小
步長係數減小因數 wu = 0.5；該數值越大，搜的範圍越精細；
最優解搜尋步長 dx[max_x]:一般為自變數取值範圍的一半；防止區域性最優解；
更新資訊素係數 k = 1；
更新資訊素因子 a;求最小值時a取e；求最大值時a取0.5；
非最優解步長係數 u = 0.7;
非最優解向最優解進化概率 p0 = 0.7;

本演算法的fun（）函式裡包含三個求最小值樣例；
三個return分別代表三個函式

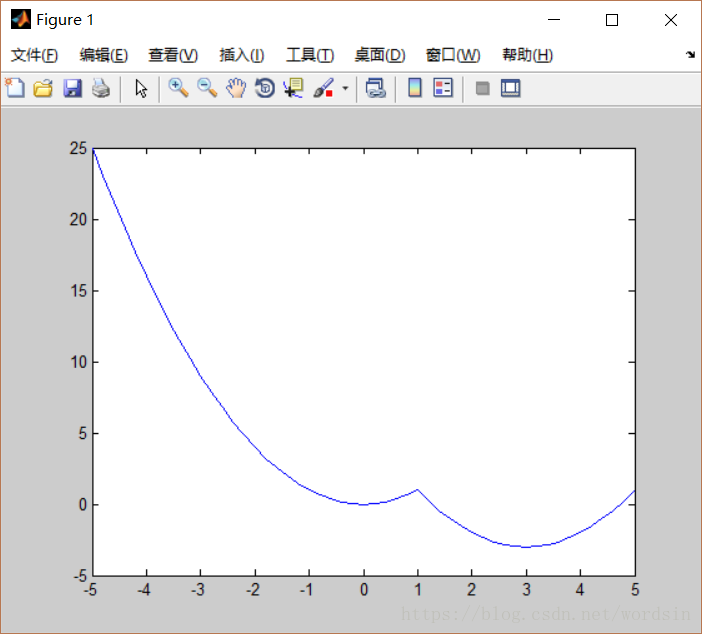
• 函式一：二維分段函式，自變數範圍[-5，5]
  

  $$f()= \begin{cases} x^2,x<=1;\\ (x-3)^2-3,x>1;\\ \end{cases}$$
  影象：
  
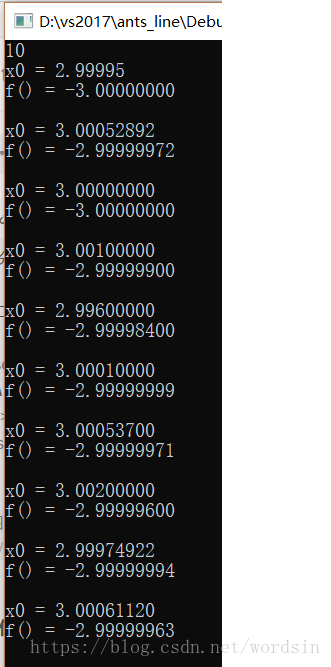
  10組測試結果：
  

• 函式二：二維複雜函式，自變數範圍[-5，5]
  

  相關推薦

  基於基本蟻群演算法解決連續優化問題

  基於基本蟻群演算法解決連續優化問題 相關連結 TSP_旅行商問題-基本蟻群演算法 基本蟻群演算法解決連續優化問題基本流程 用一個螞蟻代表一個可行解，一個螞蟻含有的資訊包括各變數值； 1、確定迭代週期； 2、確定螞蟻數；

  C++:蟻群演算法解決TSP（C++多執行緒版）

  TSP問題：旅行商問題，最短迴路。 這裡採用att48資料，鄰接矩陣全部取整數，原資料放在文後。 解決程式碼如下： //#define TEST_INPUT //#define TEST_T //#define TEST_ANT //#define TEST_VALUE #

  簡單易懂，蟻群演算法解決旅行商問題

  轉載宣告： 原文把蟻群解決旅行商問題寫的很清楚，只不過本人認為原文中有一些小錯誤，特此更改（文中紅色加粗字型為改正處），程式碼中出現的一些演算法的小問題也進行了更正（比如程式碼中的貪心演算法），程式碼也附在下面，謝謝博主的分享。 1.關於旅行商(TSP)問題及衍化

  TSP_旅行商問題-基本蟻群演算法

  TSP_旅行商問題-基本蟻群演算法 旅行商系列演算法 TSP_旅行商問題-貪心演算法 TSP_旅行商問題-模擬退火演算法 TSP_旅行商問題-遺傳演算法 TSP_旅行商問題-基本蟻群演算法 基於基本蟻群演算法解決連續優化

  記一次蟻群演算法解決TSP問題

  演算法規則 1）範圍 螞蟻觀察到的範圍是一個方格世界，螞蟻有一個引數為速度半徑(一般是3)，那麼它能觀察到的範圍就是3*3個方格世界，並且能移動的距離也在這個範圍之內。 2）摺疊環境 螞蟻所在的環境是一個虛擬的世界，其中有障礙物，有別的螞蟻，還有資訊素，資訊素有兩種，一種是找到食物的

  蟻群演算法解決tsp問題

  控制蟻群演算法走向的關鍵是資訊素，資訊素類似遺傳演算法的適應性函式，類似退火演算法的評價函式，影響著其中一隻螞蟻的下一步的選擇。 螞蟻：類似遺傳演算法的染色體，就是一條解，在tsp問題中螞蟻的路徑就是tsp的解。 資訊素：評價函式，與路徑成反比 螞蟻數量：一次迭代有多少隻螞

  ACO蟻群演算法解決TSP旅行商問題

  前言 蟻群演算法也是一種利用了大自然規律的啟發式演算法，與之前學習過的GA遺傳演算法類似，遺傳演算法是用了生物進行理論，把更具適應性的基因傳給下一代，最後就能得到一個最優解，常常用來尋找問題的最優解。當然，本篇文章不會主講GA演算法的，想要了解的同學可以檢視，我的和遺傳演算

  CMA-ES演算法解決連續優化問題

  一、演算法介紹 CMA-ES是Covariance Matrix Adaptation Evolutionary Strategies的縮寫，中文名稱是協方差矩陣自適應進化策略，主要用於解決連續優化問題，尤其在病態條件下的連續優化問題。進化策略演算法主要作為求

  2018-4-8蟻群演算法---包子陽《智慧優化演算法以及Matlab實現》第五章

  資料來源：《智慧優化演算法以及matlab實現》包子陽  餘繼周 編著第五章-----蟻群演算法是一種元啟發式優化演算法（自己理解：就是作為群體的單位個體也就是元，在裡面充當著隨機的選擇搜尋的方向，有助於全域性勘探）啟發：自然界的螞蟻有能力在沒有然和提示的情況下找到從巢穴矩離

  基於蟻群演算法求解求解TSP問題（JAVA）

  一、TSP問題 TSP問題（Travelling Salesman Problem）即旅行商問題，又譯為旅行推銷員問題、貨郎擔問題，是數學領域中著名問題之一。假設有一個旅行商人要拜訪n個城市，他必須選擇所要走的路徑，路徑的限制是每個城市只能拜訪一次，而且最後要回到原來出發的

  蟻群演算法學習

  ** 蟻群演算法的基本原理（簡單概括）： ** 剛開始螞蟻按照同等概率選擇各條路徑。 螞蟻在經過的路徑下留下資訊素。 短的路徑螞蟻會率先找到食物源，因此資訊素濃度偏大。 由於資訊素的揮發，較長路徑上的資訊素逐漸消失 特點：正反饋；不容易陷入區域

  【機器學習筆記35】蟻群演算法

  【參考資料】 【1】《蟻群演算法原理及其應用》 【2】測試資料: https://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/att48.tsp.gz 演算法原理（以TSP問題為例） （1）引數初始化。令時間t=0和迴圈次數

  蟻群演算法matlab

  （一）蟻群演算法的由來 蟻群演算法最早是由Marco Dorigo等人在1991年提出，他們在研究新型演算法的過程中，發現蟻群在尋找食物時，通過分泌一種稱為資訊素的生物激素交流覓食資訊從而能快速的找到目標，據此提出了基於資訊正反饋原理的蟻群演算法。 蟻群演算法的基本思想來源於自然界螞

  智慧演算法---蟻群演算法

    1 蟻群演算法及其基本思想 蟻群演算法是一種智慧優化演算法，通過蟻群優化求解複雜問題，ACO在離散優化問題方面有比較好的優越性。     基本思想（以旅行商問題為例）       &nbs

  何為啟發式演算法——退火演算法，蟻群演算法，遺傳演算法

  一、退火演算法 模擬退火演算法來源於固體退火原理，將固體加溫至充分高，再讓其徐徐冷卻，加溫時，固體內部粒子隨溫升變為無序狀，內能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達到平衡態，最後在常溫時達到基態，內能減為最小。 模擬退火演算法新解的產生和接受

  蟻群演算法原理詳解和matlab程式碼

  1原理： 螞蟻在尋找食物源的時候，能在其走過的路徑上釋放一種叫資訊素的激素，使一定範圍內的其他螞蟻能夠察覺到。當一些路徑上通過的螞蟻越來越多時，資訊素也就越來越多，螞蟻們選擇這條路徑的概率也就越高，結果導致這條路徑上的資訊素又增多，螞蟻走這條路的概率又增加，生生

  旅行商問題TSP（蟻群演算法Java）

  旅行商問題，即TSP問題（Traveling Salesman Problem）是數學領域中著名問題之一。假設有一個旅行商人要拜訪N個城市，他必須選擇所要走的路徑，路徑的限制是每個城市只能拜訪一次，而且最後要 回到原來出發的城市。路徑的選擇目標是要求得的路徑路程為所有路徑之中

  PSO解決TSP問題（粒子群演算法解決旅行商問題）--python實現

  歡迎私戳關注這位大神！ 有任何問題歡迎私戳我->給我寫信 首先來看一下什麼是TSP： The travelling salesman problem (TSP) asks the following question: "Given a list

  有限級資訊素蟻群演算法

  有限級資訊素蟻群演算法使用路徑等級作為資訊素更新的依據，相比於傳統的蟻群演算法，捨棄了目標函式作為資訊素更新的依據這一方法。在TSP問題中，目標函式實際就是路徑長度，在傳統的蟻群演算法中資訊素更新量為Q/f(x)，其中Q為某一常數，而f(x)就是目標函式值，即路徑長度。而在有限級資訊素蟻群演算法中在

  【機器學習】利用蟻群演算法求解旅行商（TSP）問題

  如果喜歡這裡的內容，你能夠給我最大的幫助就是轉發，告訴你的朋友，鼓勵他們一起來學習。 If you like the content here, you can give me the greatest help is forwarding, tell you