@codeforces - [email protected] Oleg and chess
目錄
@description - [email protected]
給定一個 n*n 的棋盤,並劃定一些不能放棋子的矩形區域。
現在要在棋盤上放最多的車(讀作 ju),使得這些車兩兩之間不會攻擊。
input:
第一行整數 n ——棋盤邊長(1 <= n <= 10000)。
第二行整數 q ——劃定的矩形個數(0 <= q <= 10000)。
接下來 q 行,每一行都是 x1, y1, x2, y2(1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= n),描述矩陣的左下角與右上角。
保證矩形兩兩不會相交。
output:
輸出最多的車的個數。
sample input:
5
5
1 1 2 1
1 3 1 5
4 1 5 5
2 5 2 5
3 2 3 5
sample output
3
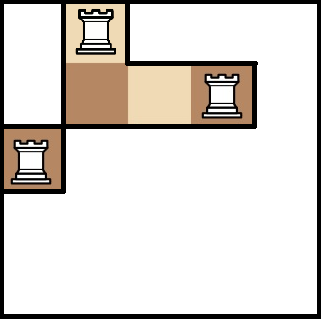
sapmle explain:
如圖。
@[email protected]
一道網路流題。
一道建模極其簡單,建圖極其噁心的網路流題。
@part - [email protected]
考慮建模。棋盤是一個很經典的二分圖,可以是黑白染色建模,也可以是行列建模。考慮到車的攻擊方式是同行同列攻擊,所以我們選擇後者。
假如某一個格子(i, j)沒有被劃定不能放車,我們就第 i 行與第 j 列連邊。再跑一個最大匹配就可以求出最多放置多少車了。
然而顯然是會 TLE 的,而且還會 T 的很慘,慘兮兮。
@part - [email protected]
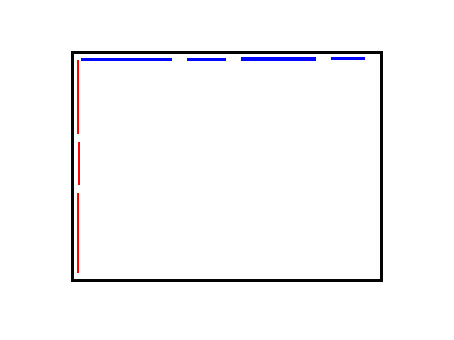
優化建圖的話,因為劃定的是規則的矩形,所以我們考慮用線段樹來優化建圖。
如圖是一個內部完全沒有限制的矩形,我們用行、列兩棵線段樹將它的兩個橫豎的邊界拆成log n條線段樹上的線段:
然後橫著的和豎著的兩兩連邊,連 log^2 n 條邊【圖片略鬼畜】:
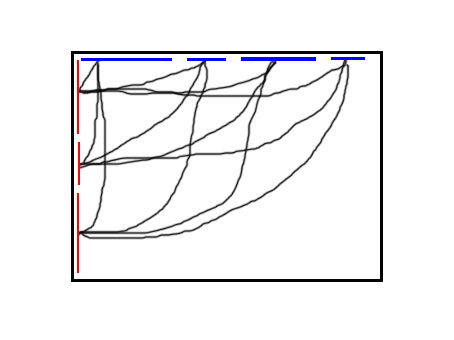
這樣就處理完了一個沒有限制的矩形。
最後:兩棵線段樹的底層端點,一棵連 S,一棵連 T,容量都為 1。線段樹內部的父子連容量為 inf 的邊。
@part - [email protected]
然而問題又來了:我們給定的是限制的矩形區域。
所以,我們必須把原棋盤切割成若干個內部沒有限制的矩形,才能運用上面所提到的優化。
怎麼切?下面是一個比較顯然的思路:
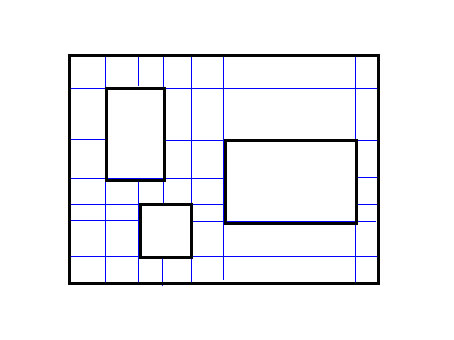
即對於每一個矩形,它的上下左右邊界往兩邊割。
然而,如果下面這個圖……
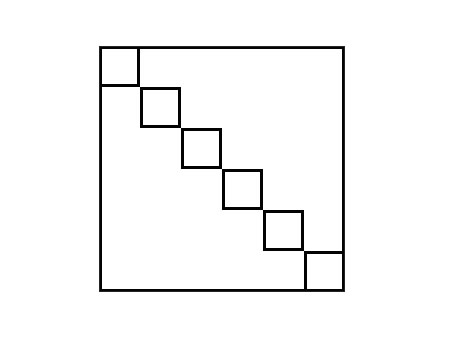
直接卡成 O(n^2)。
我們發現上面的那種切割方法,有很多小矩形是可以合併成大矩形。所以我們優化一下切割方法:
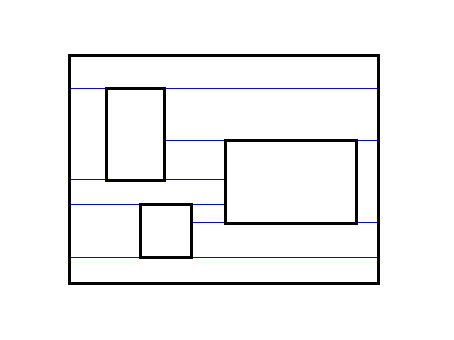
即上下邊界往兩邊切,遇到其他矩形的邊界或棋盤的邊界,則停下來。
這樣切,可以證明最多隻會分出 4*n 個矩形。
怎麼證明呢?【感性理解】每一個矩形的上下邊界向左右各引一條線,一共 4 條線,每條線可以把一個矩形切割成兩個矩形,相當於多增加了 4 個矩形。所以最多 4n 個矩形。
@part - [email protected]
OK 現在來看看怎麼實現切割。
我們用掃描線演算法,從左往右掃描。對於每一行,維護掃描線左邊距離掃描線最近的矩形邊界。如圖,我們維護的就是左邊的那彎彎曲曲的曲線:
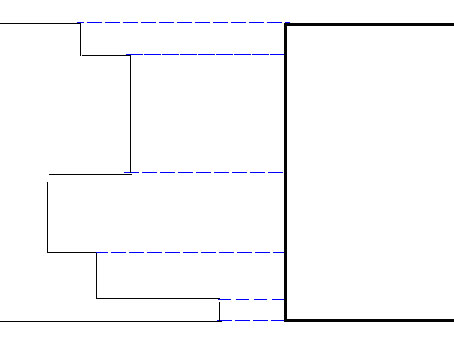
假如遇到矩形左邊界,我們就從這個矩形的上邊界開始往下暴力遍歷(對你沒聽錯就是暴力遍歷,這樣的確是 O(n^2) 的,但是其實 n 不大,對吧)。假如遇到不平坦的地方(對應到程式碼中就是相鄰兩行維護的東西不相等),則說明又產生了新的矩形。我們就進行線段樹建圖。
假如遇到矩形右邊界,更新 “掃描線左邊距離掃描線最近的矩形邊界”。
注意,這個演算法是基於矩陣不相交的前提的。
@accepted [email protected]
口胡完畢。至於程式碼量,我不清楚我不知道,大家自己慢慢調,總會調出來的 qwq。
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 10000;
const int MAXM = 100000;
const int MAXK = 2000000;
const int INF = (1<<30);
struct FlowGraph{
struct edge{
int to, cap, flow;
edge *nxt, *rev;
}edges[2*MAXK + 5], *adj[MAXM + 5], *ecnt=&edges[0];
int S, T, d[MAXM + 5], vd[MAXM + 5];
void addedge(int u, int v, int c) {
edge *p = (++ecnt);
p->to = v, p->cap = c, p->flow = 0;
p->nxt = adj[u], adj[u] = p;
edge *q = (++ecnt);
q->to = u, q->cap = 0, q->flow = 0;
q->nxt = adj[v], adj[v] = q;
p->rev = q, q->rev = p;
}
int aug(int x, int tot) {
if( x == T ) return tot;
int mind = T+1, sum = 0;
for(edge *p=adj[x];p!=NULL;p=p->nxt) {
if( p->cap > p->flow ) {
if( d[p->to] + 1 == d[x] ) {
int del = aug(p->to, min(tot-sum, p->cap-p->flow));
p->flow += del, p->rev->flow -= del, sum += del;
if( d[S] == T+1 ) return sum;
if( sum == tot ) return sum;
}
mind = min(mind, d[p->to]);
}
}
if( sum == 0 ) {
vd[d[x]]--;
if( vd[d[x]] == 0 )
d[S] = T+1;
d[x] = mind + 1;
vd[d[x]]++;
}
return sum;
}
int max_flow() {
int flow = 0;
while( d[S] < T+1 )
flow += aug(S, INF);
return flow;
}
}G;
int cnt = 0;
struct SegmentTree{
int le, ri, num;
}t[2][4*MAXN + 5];
vector<int>v[2];
void build_segtree(int x, int l, int r, int n) {
t[n][x].le = l, t[n][x].ri = r, t[n][x].num = (++cnt);
if( l == r ) return ;
int mid = (l + r) >> 1;
build_segtree(x<<1, l, mid, n);
build_segtree(x<<1|1, mid+1, r, n);
}
void build_edge_segtree(int x, int n) {
if( t[n][x].le == t[n][x].ri ) {
if( n == 0 ) G.addedge(G.S, t[n][x].num, 1);
else G.addedge(t[n][x].num, G.T, 1);
}
else {
if( n == 0 ) {
G.addedge(t[n][x<<1].num, t[n][x].num, INF);
G.addedge(t[n][x<<1|1].num, t[n][x].num, INF);
}
else {
G.addedge(t[n][x].num, t[n][x<<1].num, INF);
G.addedge(t[n][x].num, t[n][x<<1|1].num, INF);
}
build_edge_segtree(x<<1, n);
build_edge_segtree(x<<1|1, n);
}
}
void get_segment(int x, int l, int r, int n) {
if( l <= t[n][x].le && t[n][x].ri <= r ) {
v[n].push_back(t[n][x].num);
return ;
}
if( l > t[n][x].ri || r < t[n][x].le )
return ;
get_segment(x<<1, l, r, n);
get_segment(x<<1|1, l, r, n);
}
void build_edge_area(int x1, int y1, int x2, int y2) {
if( x1 > x2 || y1 > y2 ) return ;
v[0].clear(), v[1].clear();
get_segment(1, x1, x2, 0);
get_segment(1, y1, y2, 1);
for(int i=0;i<v[0].size();i++)
for(int j=0;j<v[1].size();j++)
G.addedge(v[0][i], v[1][j], INF);
}
struct node{
int le, ri;
node(int _l=0, int _r=0):le(_l), ri(_r){}
};
vector<node>vec[MAXN + 5][2];
int left[MAXN + 5];
int main() {
int n, q;
scanf("%d%d", &n, &q);
build_segtree(1, 1, n, 0); build_segtree(1, 1, n, 1); G.T = cnt + 1;
build_edge_segtree(1, 0); build_edge_segtree(1, 1);
for(int i=1;i<=q;i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &y1, &x1, &y2, &x2);
vec[x1][0].push_back(node(y1, y2));
vec[x2][1].push_back(node(y1, y2));
}
vec[n+1][0].push_back(node(1, n));
for(int i=1;i<=n+1;i++) {
for(int j=0;j<vec[i][0].size();j++) {
int lst = vec[i][0][j].le;
for(int k=vec[i][0][j].le+1;k<=vec[i][0][j].ri;k++)
if( left[k] != left[k-1] )
build_edge_area(left[k-1]+1, lst, i-1, k-1), lst = k;
build_edge_area(left[vec[i][0][j].ri]+1, lst, i-1, vec[i][0][j].ri);
}
for(int j=0;j<vec[i][1].size();j++)
for(int k=vec[i][1][j].le;k<=vec[i][1][j].ri;k++)
left[k] = i;
}
//注意我們必須要先處理矩形的左邊再處理矩形的右邊,不然遇到寬度為 1 的矩形就直接 GG 了。
int ans = G.max_flow();
printf("%d\n", ans);
}@[email protected]
一開始我寫的從上往下的掃描線,結果發現 TLE 在 144th 組資料上。
氣的我一怒之下把掃描線改成從左往右的。
然後……它就 AC 了???
聽說機房裡的另外一個人遇到了一樣的情況,然後他把 isap 換成了 dinic 才過的。
好玄妙啊,果然是網路流。
