【Unity】從零開始的布料模擬
前言
遊戲引擎中對布料的模擬,通常採用基於物理方法的質點-彈簧模型(Mass-Spring Model)。
為了實現定製的效果,本文將基於簡化版的模型進行物理飄動的模擬。
這裡是一篇物理模擬的文章,包含了本文中使用的大部分理論。
基本原理
定義粒子(Particle)節點,粒子是物理模擬的基本單位,物理模擬的結果就是驅動這些節點的位置變化。物理模擬包含的要素大致分為:外力結算、約束結算、碰撞結算,其中約束結算又包含了很多種約束。
這些物理模擬之間存在大量的耦合,比如物體受重力的同時又受到來自另一個粒子的彈性約束,兩者之間是互相影響的。但對於遊戲模擬而言,保證足夠的可信度即可,可以容忍些許的精度缺失。所以採用鬆弛法(Relaxation)迭代,即每個方法獨立結算,通過多次迭代達到較高精度。
物理模型
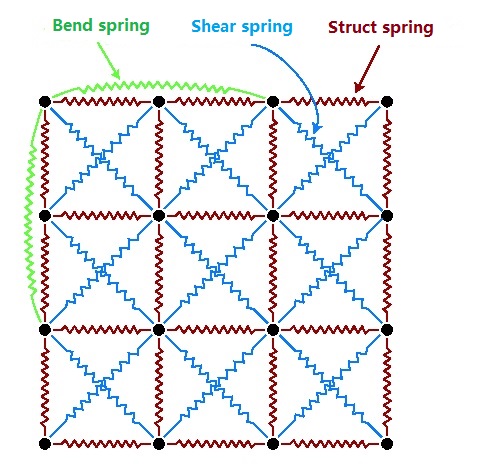
質點-彈簧模型(Mass-Spring Model)質點彈簧模型是將質點用彈簧連線,發生位移時,每個質點都受到彈性約束,這種模型的有點在於簡單、效率高。
三種彈簧分別對應結構力(拉力、壓力)、剪下力、彎曲力的結算。
Unity中的Cloth元件就是將模型的頂點作為質點,進而實現的飄動效果。
一種簡化的鏈條模型
本文的實現方法類似Dynamic Bone、Swing Bone、PhysicsBone等外掛,是將骨骼節點作為粒子(Particle),通過骨骼節點驅動蒙皮網格來實現飄動效果。由於質點的分佈並非是整齊的,本文將從單鏈式的骨骼結構開始實現,不同於質點彈簧模型,這種結構沒有質點彈簧模型的剪下彈簧。
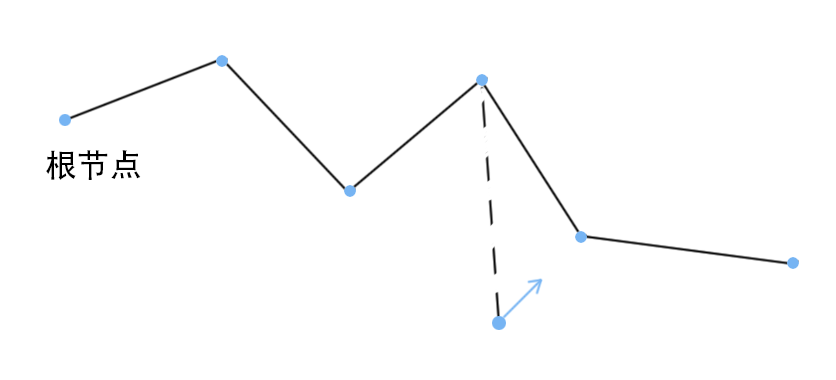
本文先從最簡化的結構開始,一個骨骼鏈條,將每個骨骼節點作為粒子(Particle)。
第一個粒子是根節點,根節點位置固定(掛載在其他運動的物體上,如動畫系統),其他 粒子受本地形狀約束,即每次變化粒子都會保持一定的本地拓撲結構。
物理模型在Unity中
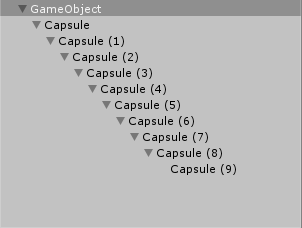
先按照最簡單的骨骼結構處理,只有父子級的單鏈結構,這裡就不使用蒙皮網格了,可以在Unity中建立如下結構進行試驗
這是由一系列膠囊體組成的層級父子級結構,模擬鏈式骨骼驅動模型運動,這裡不能用球體代替,因為我們需要觀察轉動資訊,蒙皮網格是被位置與轉動共同驅動的。
Verlet Integration
Verlet演算法是經典力學中的一種最為普遍的積分方法,被廣泛運用在分子運動模擬(Molecular Dynamics Simulation),行星運動以及織物變形模擬等領域。Verlet演算法本質上是對牛頓第二定律的泰勒展開,精度為O(4), 比尤拉方法精度更高,穩定度更好,且計算複雜度不比顯式尤拉方法高多少。
簡單的帶阻尼Verlet Integration:
Verlet Integration的優勢在於不必計算與保留速度資訊,可以很方便的加入各種約束,缺點是每次泰勒展開的微元Δt必須是固定的,即每次迭代的時間不長是固定的。
本地形狀約束
約束文中的鏈式結構的最簡單方法是保持本地的拓撲結構,即強制讓粒子回到父節點的原始相對位置(LocalPosition)上。
本文采用鬆弛法,所以可以自由新增約束,後文也會介紹更多約束型別。
碰撞結算
碰撞處理的最簡單方法是將發生碰撞的點,移動至最近的碰撞表面,可以將碰撞視為約束的一種。
虛擬碼
using System.Collections.Generic;
using UnityEngine;
using System;
public class SpringarmParticleSystem : MonoBehaviour
{
/// 根節點
public Transform root;
/// 更新頻率,每秒的次數
public float updateRate;
/// 碰撞集合
public SphereCollider[] colliders;
/// 粒子集合
public List<Particle> particles;
/// 定義基本粒子
public class Particle
{
/// 質點
public Transform transform;
/// 引數,多個
public float coefficient;
/// Verlex積分儲存的位置
public Vector3[] positions;
/// 相對資訊,多個
public Vector3 relativeValue;
}
void Start()
{
SetupParticles();
}
/// 初始化粒子組
private void SetupParticles(){}
private void LateUpdate()
{
UpdatesParticles();
}
/// 根據主迴圈幀時間確定迭代次數,迭代完成後應用更改,每幀只應用1次
private void UpdatesParticles()
{
for (int i = 0; i < iterationTime; i++)
{
UpdateParticles();
}
Apply();
}
/// 鬆弛法迭代
/// </summary>
private void UpdateParticles()
{
for (int i = 0; i < particles.Count; i++)
{
///VerletIntegration
VerletIntegration(i);
}
for (int i = 1; i < particles.Count; i++)
{
///本地形狀約束
ShapeKeeping(i);
///約束
Resistance(i);
///約束
Resistance(i);
///碰撞
CollisionSolve(i);
///約束
Resistance(i);
}
}
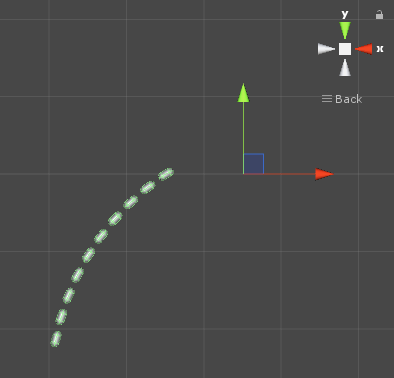
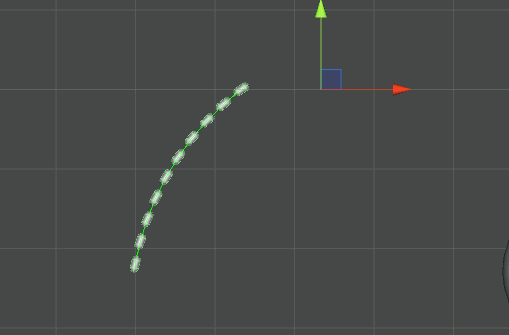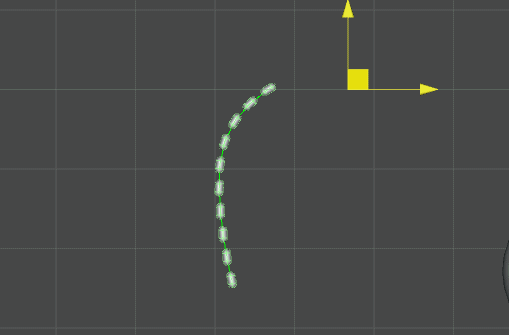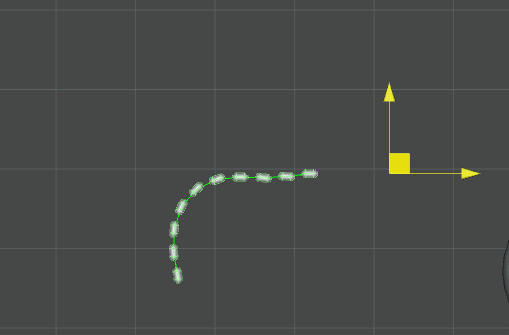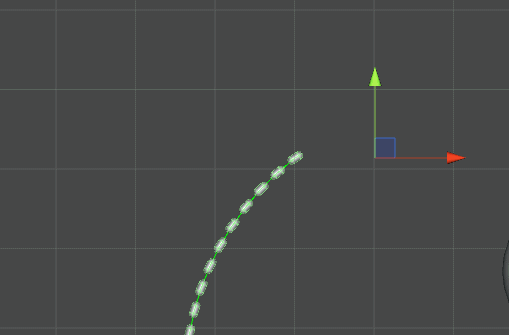
} 至此,我們能做到上圖的效果,可以看出每個節點能夠實現基本的飄動與形狀保持,但節點只有位置發生變化,角度(Rotation)沒有改變。在蒙皮骨骼中,需要改變節點的轉動位置,我們需要做的是使子節點指向父節點向量在父節點座標系下方向不變,要做到這點還要保持位置變化,就要在改變位置之前改變父節點的Rotation。
至此,我們能做到上圖的效果,可以看出每個節點能夠實現基本的飄動與形狀保持,但節點只有位置發生變化,角度(Rotation)沒有改變。在蒙皮骨骼中,需要改變節點的轉動位置,我們需要做的是使子節點指向父節點向量在父節點座標系下方向不變,要做到這點還要保持位置變化,就要在改變位置之前改變父節點的Rotation。處理後:
引入新約束
上面的虛擬碼中鬆弛法迭代過程中,VerletIntegration之後開始了一系列的約束,完成迭代之後進行Apply(應用更改)操作。整體的執行順序是:
1、完成所有節點的運動學積分
2、完成所有節點的約束(每個節點的多個約束順序執行,之後再執行下一個節點的所有約束)
3、應用變更
可以看出越靠後的約束越容易對顯示的結果造成直接影響,所以我們要注意約束的順序,例如在碰撞約束之後,執行長度約束,避免大碰撞體積導致形體拉伸。
for (int i = 0; i < particles.Count; i++)
{
///VerletIntegration
VerletIntegration(i);
}
for (int i = 1; i < particles.Count; i++)
{
///本地形狀約束
ShapeKeeping(i);
///約束
Resistance(i);
///約束
Resistance(i);
///碰撞
CollisionSolve(i);
///約束
Resistance(i);
}不同的約束能夠組合出很多不同的效果,可以根據具體使用環境選取。
本地形狀約束:約束父節點與本節點的相對位置
彈性約束:約束父節點與本節點的相對長度
彎曲彈性約束:約束二級父節點與本節點的相對長度
同心圓過長約束:約束根節點與本節點的相對長度
反向動力學
上文的方法只改變了子節點的位置,如果需要反向動力學,則需要讓子節點對父節點產生影響,比如彈性約束中需要同時考慮一個節點的父節點與子節點對它的影響。
加入自定義約束
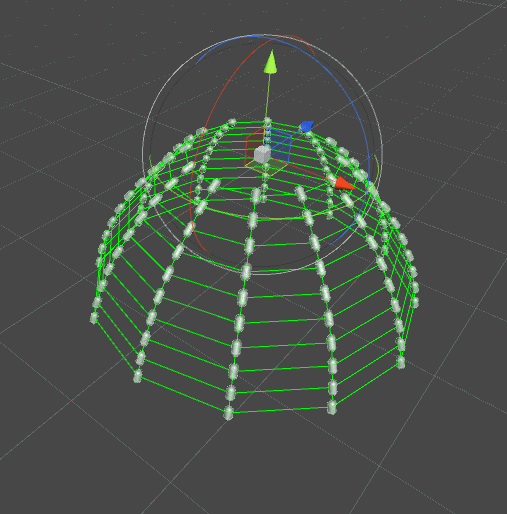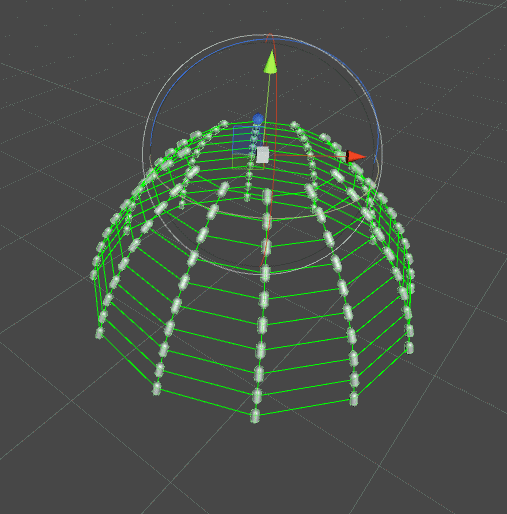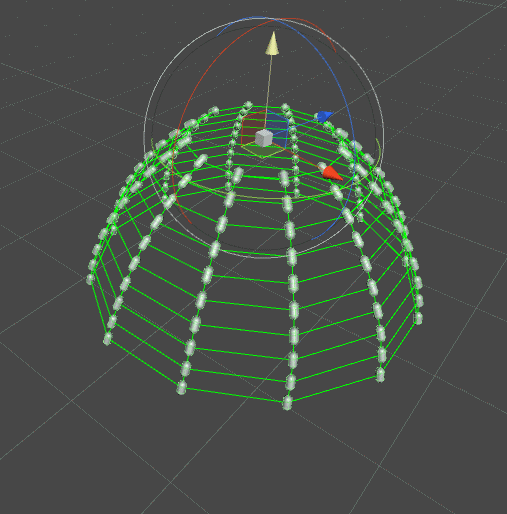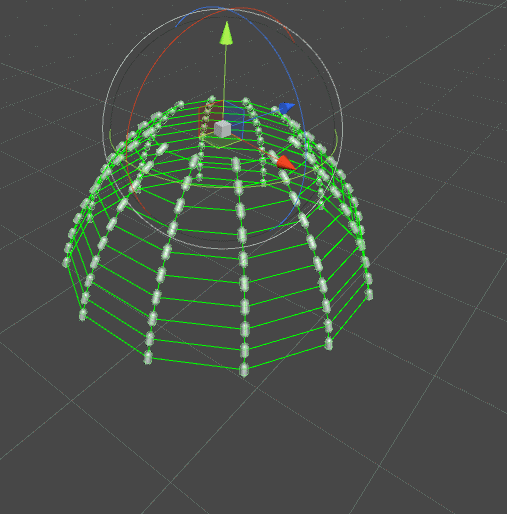
當需要模擬布料形態的物體時,文中的鏈式結構就無法滿足需求了,所以我們增加一個節點與關聯節點,在關聯節點間增加約束。如下圖類似裙襬的效果:
上面的演示是在相鄰列中加入彈性約束(綠色線條),所以遇到碰撞的列發生變化也會影響到附近沒有碰撞的列。